1.5.2: Stretching and Reflecting Transformations
- Page ID
- 14140
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Stretching and Reflecting Transformations
Understanding how changes in the equation of a function result in stretching and/or reflecting the graph of the function is a great way to take some of the mystery out of graphing more complicated equations. By recognizing the family to which a more complex equation belongs, and then identifying what changes have been made to the parent of that family, the graph of even quite detailed functions can be made much more understandable.
See if you can identify what parts of the equation: \(\ y=-\frac{1}{5} x^{2}\) represent either a stretch or a reflection of the parent function y=x2 before the examples in this section.
Stretching and Reflecting Transformations
Stretching and Compressing Graphs
If we multiply a function by a coefficient, the graph of the function will be stretched or compressed.
Given a function f(x), we can formalize compressing and stretching the graph of f(x) as follows:
- A function g(x) represents a vertical stretch of f(x) if g(x) = cf(x) and c > 1.
- A function g(x) represents a vertical compression of f(x) if g(x) = cf(x) and 0 < c < 1.
- A function h(x) represents a horizontal compression of f(x) if h(x) = f(cx) and c > 1.
- A function h(x) represents a horizontal stretch of f(x) if h(x) = f(cx) and 0 < c < 1.
Notice that a vertical compression or a horizontal stretch occurs when the coefficient is a number between 0 and 1.
Reflecting Graphs Over the y-axis and x-axis
Consider the graphs of the functions y = x2 and y = -x2, shown below.
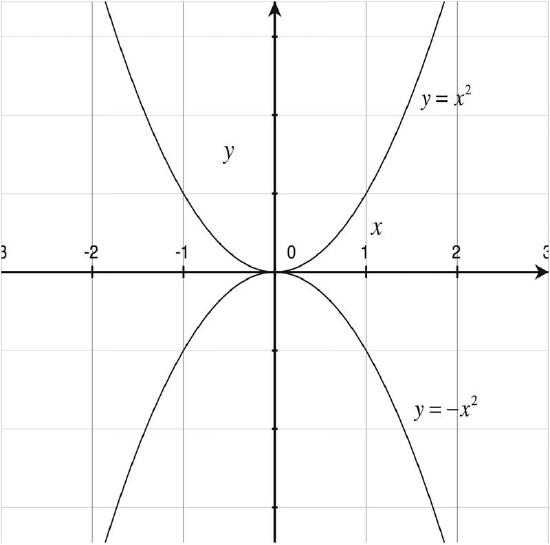
The graph of y = -x2 represents a reflection of y = x2, over the x-axis. That is, every function value of y = -x2 is the negative of a function value of y = x2. In general, g(x) = -f(x) has a graph that is the graph of f(x), reflected over the x-axis.
Solution
Earlier, you were asked a question about identifying transformations.
The function \(\ y=-\frac{1}{5} x^{2}\) is the result of transforming y=x2 by reflecting it over the x axis, because of the negative co-efficient on the x, and vertically compressing it (making it wider), because the co-efficient on the x is a fraction between 0 and 1.
Identify the graph of the function y = (3x)2.
Solution
We have multiplied x by 3. This should affect the graph horizontally. However, if we simplify the equation, we get y = 9x2. Therefore the graph if this parabola will be taller/thinner than y = x2. Multiplying x by a number greater than 1 creates a horizontal compression, which looks like a vertical stretch.
Identify the transformation described by y = ((1/2)x)2.
Solution
If we simplify this equation, we get y = (1/4) x2. Therefore multiplying x by a number between 0 and 1 creates a horizontal stretch, which looks like a vertical compression. That is, the parabola will be shorter/wider.
Sketch a graph of y = x3 and y = -x3 on the same axes.
Solution
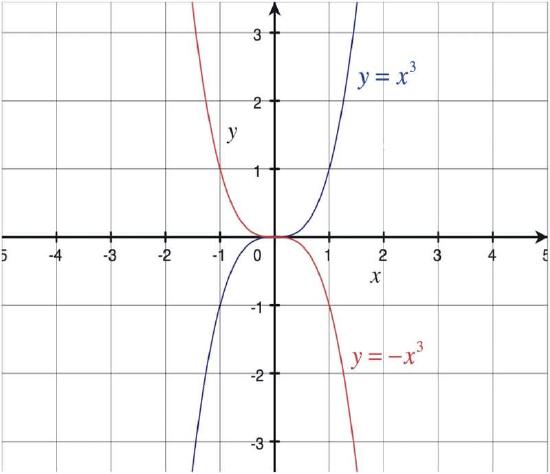
At first the two functions might look like two parabolas. If you graph by hand, or if you set your calculator to sequential mode (and not simultaneous), you can see that the graph of y = -x3 is in fact a reflection of y = x3 over the x-axis.
However, if you look at the graph, you can see that it is a reflection over the y-axis as well. This is the case because in order to obtain a reflection over the y-axis, we negate x. In other words, h(x) = f(-x) is a reflection of f(x) over the y-axis. For the function y = x3, h(x) = (-x)3 = (-x) (-x) (-x) = -x3. This is the same function as the one we have already graphed.
It is important to note that this is a special case. The graph of y = x2 is also a special case. If we want to reflect y = x2 over the y-axis, we will just get the same graph! This can be explained algebraically: y = (-x)2 = (-x) (-x) = x2.
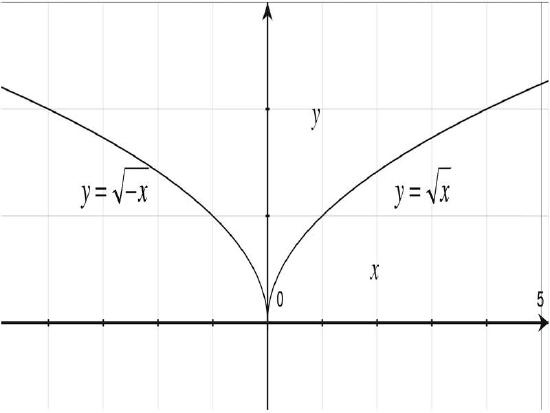
Graph the functions \(\ y=\sqrt{x} \text { and } y=\sqrt{-x}\).
Solution
The equation \(\ y=\sqrt{-x}\) might look confusing because of the -x under the square root. It is important to keep in mind that - x means the opposite of x. Therefore the domain of this function is restricted to values ≤ 0. For example, if \(\ x=-4, y=\sqrt{-(-4)}=\sqrt{4}=2\). It is this domain, which includes all real numbers not in the domain of \(\ y=\sqrt{x}\) plus zero, that gives us a graph that is a reflection over the y-axis.
In sum, a graph represents a reflection over the x-axis if the function has been negated (i.e. the y has been negated if we think of y = f(x)). The graph represents a reflection over the y-axis if the variable x has been negated.
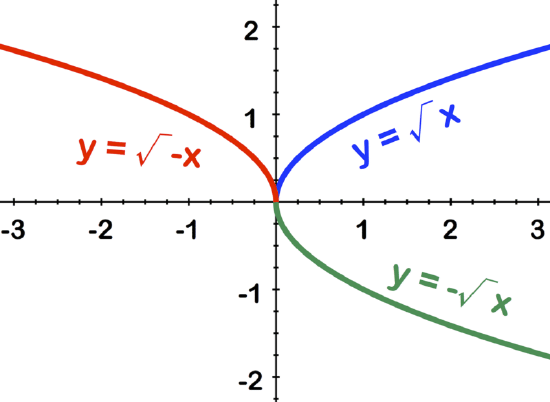
Identify the function and sketch the graph of \(\ y=\sqrt{x}\) reflected over both axes.
Solution
To reflect the graph of \(\ y=\sqrt{x}\) over both axes, the function must be negated both outside and inside the root: \(\ y=-\sqrt{-x}\). The negation (negative) outside of the root has the effect of reflecting the graph vertically, and the negation inside of the root reflects the graph horizontally. The image below shows three versions:
BLUE: \(\ y=\sqrt{x}\)
GREEN: \(\ y=-\sqrt{x}\)
RED: \(\ y=\sqrt{-x}\)
Review
- If a function is multiplied by a coefficient, what will happen to the graph of the function?
- What does multiplying x by a number greater than one create?
- What happens when we multiply x by a number between 0 and 1?
- In order to obtain a reflection over the y axis what do we have to do to x?
- How do we obtain a reflection over the x-axis?
- Write a function that will create a horizontal compression of the following:f(x)=x2+3
- Write a function that will horizontally stretch the following: f(x)=x2−6
- Rewrite the function \(\ f(x)=-\sqrt{x}\) to get a reflection over the x-axis.
- Rewrite the function \(\ f(x)=\sqrt{x}\) to get a reflection over the y-axis.
Graph each of the following using transformations. Identify the translations and reflections.
- f(x)=|x|−2
- \(\ h(x)=\sqrt{x+3}\)
- \(\ g(x)=\frac{1}{x+1}\)
- f(x)=−4x3
- h(x)=(x+3)3+1
- \(\ f(x)=\frac{1}{3}(x-3)^{2}+1\)
- \(\ f(x)=-4 \sqrt{x+1}-2\)
- \(\ f(x)=\frac{2}{3(x-2)}+\frac{1}{4}\)
Let y=f(x) be the function defined by the line segment connecting the points (-1, 4) and (2, 5). Graph each of the following transformations of y=f(x).
- y=f(x)+1
- y=f(x+2)
- y=f(−x)
- y=f(x+3)−2
The graph of y = x is shown below. Sketch the graph of each of the following transformations of y = x
- y=x+3
- y=x−2
- y=−x
Vocabulary
| Term | Definition |
|---|---|
| compression | A stretch or compression is a function transformation that makes a graph narrower or wider, without translating it horizontally or vertically. |
| Function Family | Function families are groups of functions with similarities that make them easier to graph when you are familiar with the parent function, the most basic example of the form. |
| parent function | A parent function is the simplest form of a particular type of function. All other functions of this type are usually compared to the parent function. |
| Reflecting | Reflecting a graph means to transform the graph in order to produce a "mirror image" of the original graph by flipping it across a line. |
| Reflection | Reflections are transformations that result in a "mirror image" of a parent function. They are caused by differing signs between parent and child functions. |
| stretch | A stretch or compression is a function transformation that makes a graph narrower or wider. |
| stretching | Stretching a graph means to make the graph narrower or wider. |
| Transformations | Transformations are used to change the graph of a parent function into the graph of a more complex function. |

