2.5.1: Quadratic Inequalities

Quadratic Inequalities

How would you express the following as a function?

You are supposed to mow your square-shaped lawn for your parents, but the mower only has part of a tank of gas. If you can mow 2500 sf per gallon, and the mower has approximately 2.5 gallons in it, what is the maximum length of one side of the lawn you can mow? If your lawn is 75 feet long, will you need more gas?

---

Quadratic Inequalities

Quadratic inequalities are inequalities that have one of the following forms

ax²+bx+c>0

and

ax²+bx+c<0

We can solve these inequalities by using the techniques that we have learned about solving quadratic equations. For example, consider the graph of the equation:

y=f(x)=x²+x−6

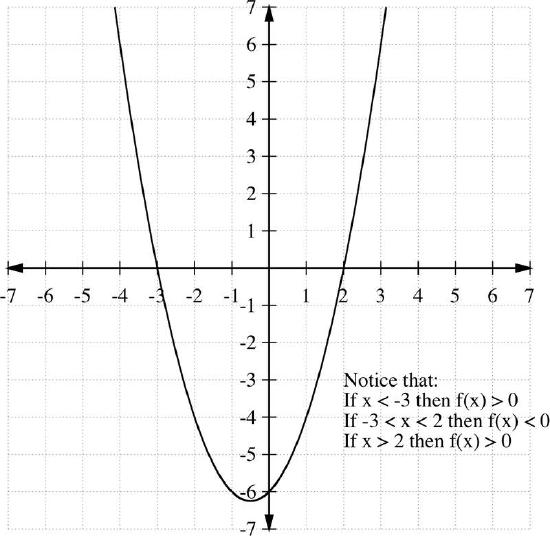[Figure1]

Notice that the curve intersects the x−axis at -3 and 2. From graph, we notice the followings

• If x<−3 then f(x)>0
• If −3<x<2, then f(x)<0
• If x>2, then f(x)>0

Therefore, x²+x−6>0 whenever x<−3 or x>2, and x²+x−6<0 when −3<x<2.

---

Examples

Example 1

Earlier, you were given a question about mowing a lawn.

If you can mow 2500 sf of grass per gallon of gas, and the mower has 2.5 gallons in it, what is the maximum length of one side of the lawn you can mow?

If your lawn is 75 ft long, will you need more gas?

Solution

We know that the function S²<6250 describes the possible side lengths of square shapes you could mow before running out of gas (if you're having trouble understanding why, see Example 4 for a similar process).

Solving for S gives:

\(\ \begin{array}{l}
\sqrt{s^{2}}=\sqrt{6250} \\
s=79
\end{array}\)

With 2.5 gal of gas, you could mow a square up to apx 79 ft on each side.

You should not need more gas if the lawn is only 75 ft long on each side.

Example 2

What is the solution set of the inequality 2x²+7x−4<0?

Solution

It is best to graph the function f(x)=2x²+7x−4 and look for the values of x such that the inequality f(x)<0 is true.

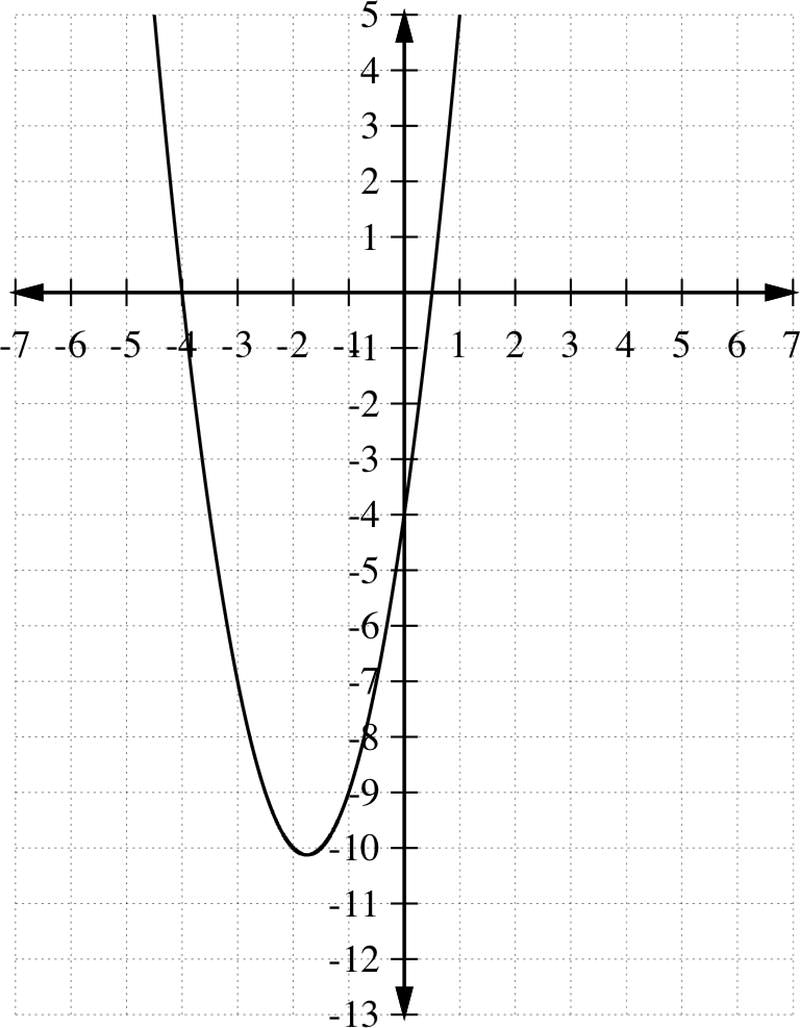
Thus from graph, 2x²+7x−4<0 only if

\(\ -4<x<\frac{1}{2}\)

So the solution set is \(\ x \in\left(-4, \frac{1}{2}\right)\) or in set builder notation, \(\ \left\{x \mid-4<x<\frac{1}{2}\right\}\)

Although the method of graphing to find the solution set of an inequality is easy to follow, another algebraic method can be used. The algebraic method involves finding the x−intercepts of the graph and then dividing the x−axis into intervals separated by the x−intercepts. The examples below illustrate the method.

Example 3

Find the solution set of the quadratic inequality x²+2x−8>0 without graphing.

Solution

To find the solution set without graphing, first factor:

x²+2x−8=0

(x+4)(x−2)=0

Recalling the zero product rule, we can see that the two solutions to this quadratic equation are x=−4 and x=2, thus, the x−intercepts of the function f(x)=x²+2x−8 are -4 and 2.

These points divide the x−axis into three intervals: (−∞,−4)|(−4,2)|(2,∞). We can choose a test point from each interval, substitute it into f(x) and see if the function is negative or positive with that value as x. This procedure can be simplified by making a table as shown below:

Interval	Test Point	Is x^2+2x−8 positive or negative?	Part of Solution set?
(−∞,−4)	−5	+	yes
(−4,2)	1	−	no
(2,+∞)	3	+	yes

From the table, we conclude that since x²+2x−8>0 if and only if x<−4 and x>2. The solution set can also be written as:

x∈(−∞,−4)∪(2,+∞)

Some problems in science involve quadratic inequalities. The example below illustrates one such application.

Example 4

A rectangle has a length 10 meters more than twice the width. Find all of the possible widths that result in the area of the rectangle not exceeding 100 squared meters.

Solution

Let w be the width of the rectangle and l its length. Given the information in the question, we can say:

l=10+2w

Then we can use the formula for the area of a rectangle:

area=l×w

Substituting 10+2w in for l gives:

area=w×(10+2w)

The area cannot exceed 100 m², so

10w+2w²<100

or

2w²+10w−100<0

Simplify by dividing both sides by 2:

w²+5w−50<0

Factor the trinomial:

w²+5w−50=(w+10)(w−5)

So the partition points are 5 and -10, which means we have three intervals. Since width cannot be negative, we can safely ignore -10. That means the maximum area is 100 m²

∴w<5.

The width must be less than 5 meters.

Example 5

Find the solution set of the inequality x²≤16.

Solution

Set the function equal to zero:

x²−16=0

Factor to find the critical values (points where the graph crosses the x axis, thereby changing signs):

(x−4)(x+4)=0

By the zero product rule: x=4 or x=−4

That gives us three sections on the graph:

x≤−4

−4≤x≤4

4≤x

Test one sample value from each division to identify possible solution sets.

Set	x≤−4	−4≤x≤4	4≤x
Test value	−5		5
f(x) true with value?	4⋅(−5)^2=100≰16 ∴No	4⋅0^2=0≤16 ∴Yes	4⋅5^2=100≰16 ∴No

Therefore the solution set is −4≤x≤4.

Example 6

Graph the solution set: (x−3)(x+4)≥0.

Solution

The solutions to (x−3)(x+4)≥0 can be identified with the rules for multiplying negative numbers:

Recall from Pre-Algebra that an even number of negatives yields a positive answer, and an odd number of negatives yields a negative answer.

Since (x−3)(x+4)≥0 we know we need a positive answer or zero.

Therefore either:

Case #1: (x−3)≥0→x≥3 and (x+4)≥0→x≥−4

or

Case #2: (x−3)≤0→x≤3 and (x+4)≤0→x≤−4

Since any number greater than 3 is already greater than -4, from Case #1 we get: x≥3

Since any number less than -4 is already less than 3, from Case #2 we get x≤−4

Therefore our answer is x≤−4 or x≥3

In set notation: x∈(−∞,−4]∪[3,+∞)

To graph this information, we draw a line graph, and mark the values that x can be, with solid dots on the end numbers to indicate that those values are included.

Visually that is:

" frameborder="0" height="450px" name="99198" src="https://www.ck12.org/flx/show/video/...ties-Example-2" thumbnailurl="" title="VideoObject?hash=f688e36d565e0820730d1d47d13380a6" uploaddate="2016-07-06 16:34:48" width="95%">

---

Review

Graph the solutions sets below on a number line:

1. x<3 or x>4
2. x≥−5 and x≥3
3. x<6 and x≥−2
4. x>7 or x≥−4
5. x≤−8 and x>3

Identify critical points, solve, and graph:

6. x²+9x>−14
7. x²−5x≤50
8. x²+2x≤48
9. \(\ x-\frac{20}{x}-8<0\) (hint: multiply both sides by x first)
10. \(\ x+10 \geq-\frac{21}{x}\)
11. (x+6)(x−3)>0
12. (x−8)(x+1)>0
13. x²−x≥90
14. 3x²−23x≤8
15. x²+x−6>0

---

Review (Answers)

To see the Review answers, open this PDF file and look for section 2.9.

---

Vocabulary

Term	Definition
Critical Values	The critical values are the x−intercepts of a quadratic function.
interval	An interval is a specific and limited part of a function.
quadratic inequality	A quadratic inequality is a quadratic expression that is specified to be greater or lesser than a given value.
Roots	The roots of a function are the values of x that make y equal to zero.
Zero Product Rule	The zero product rule states that if the product of two expressions is equal to zero, then at least one of the original expressions much be equal to zero.

---

Image Attributions

1. [Figure 1]
   Credit: CK-12 Foundation;Desmos
   Source: Desmos