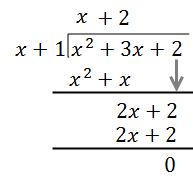2.6.1: Long Division of Polynomials

Last updated
Save as PDF

Page ID: 14227

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

Long Division and Synthetic Division

Can you divide the following polynomials?

\(\ \frac{x^{2}-5 x+6}{x-2}\)

Long Division and Synthetic Division

Polynomial Long Division

Whenever you want to divide a polynomial by a polynomial, you can use a process called polynomial long division. This process is similar to long division for regular numbers. Look at the problem below:

\(\ \frac{\left(x^{2}+3 x+2\right)}{(x+1)}\)

This is the same as the division problem below:

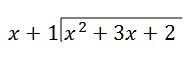
f-d_514f0f506c20ad0916f4b6d8b92dc800f7b50f37c7062f8f5369a3c4+IMAGE_TINY+IMAGE_TINY.png

Step 1: Divide the first term in the numerator (x²) by the first term in the denominator (x). Put this result above the division bar in your answer. In this case, \(\ \frac{x^{2}}{x}=x\).

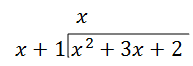
f-d_04c47d5c17bab8c46f5a87659c805522857a8ce241e1ac06c25c47e7+IMAGE_TINY+IMAGE_TINY.png

Step 2: Multiply the denominator (x+1) by the result from Step 1 (x), and put the new result below your numerator. Then, subtract to get your new polynomial. This is the same process as in regular number long division!

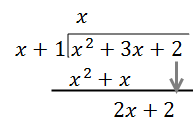
f-d_d1d39546d223a6d1667765a8cae7848cb6333772a056822a1e460de2+IMAGE_TINY+IMAGE_TINY.png

Step 3: Divide the first term in the new polynomial (2x) by the first term in the denominator (x). Put this result above the division bar in your answer. Multiply, subtract, and repeat this process until you cannot repeat it anymore.

Therefore: \(\ \frac{\left(x^{2}+3 x+2\right)}{(x+1)}=(x+2)\)

Synthetic Division

Synthetic division is another method of dividing polynomials. It is a shorthand of long division that only works when you are dividing by a polynomial of degree 1. Usually the divisor is in the form (x±a). In synthetic division, unlike long division, you are only concerned with the coefficients in the polynomials. Consider the same problem as above:

f-d_514f0f506c20ad0916f4b6d8b92dc800f7b50f37c7062f8f5369a3c4+IMAGE_TINY+IMAGE_TINY.png

Step 1: Write the coefficients in an upside down division sign.

f-d_673fbc23f79722f395795c50462e8245f0a8d1aef56a464444d7ad78+IMAGE_TINY+IMAGE_TINY.png

Step 2: Put the opposite of the number from the divisor to the left of the division symbol. In this case, the divisor is x+1, so you will use a −1.

f-d_79055d60db9659bd43145a43c8e339da74f47d25770ef1f313926a38+IMAGE_TINY+IMAGE_TINY.png

Step 3: Take your leading coefficient and bring it down below the division symbol.

f-d_ce9450e8c5098a25b1c2bc43a8e9c1d05752bf34d902d314f66dafcc+IMAGE_TINY+IMAGE_TINY.png

Step 4: Multiply this number by the number to the left of the division symbol and place it in the next column. Add the two numbers together and place this new number below the division sign.

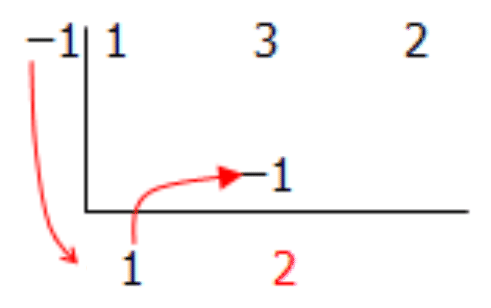f-d_6e63383e009344f7034dbf47176b190b954e5ee312497ab9aa692214+IMAGE_TINY+IMAGE_TINY.png

Step 5: Multiply this second number by the number to the left of the division symbol and place it into the third column. Add the two numbers together and place this new number below the division sign.

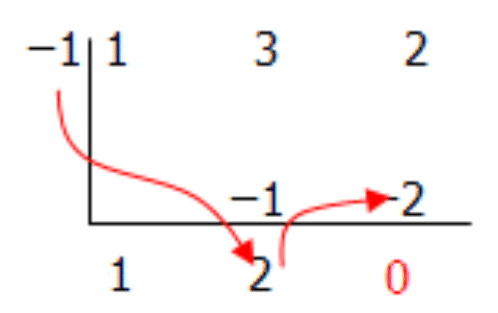f-d_02bc84fbae4e2f0f1a8a8fcb9c7dd5f84fdfb855b373c8186ec494b6+IMAGE_TINY+IMAGE_TINY.png

The numbers below the division sign represent your coefficients. Therefore,

\(\ \frac{\left(x^{2}+3 x+2\right)}{(x+1)}=(x+2)\)

Examples

Example 1

Earlier, you were asked to divide polynomials:

\(\ \frac{x^{2}-5 x+6}{x-2}\)

Solution

You can use long division or synthetic division.

Long Division:

Step 1: Divide the first term in the numerator by the first term in the denominator, put this in your answer. Therefore \(\ \frac{x^{2}}{x}=x\).

\(\ \begin{array}{c}
\textcolor{red}x\\
(x-2)|\overline{x^2 -5x + 6}
\end{array}\)

Step 2: Multiply the denominator by this number (variable) and put it below your numerator, subtract and get your new polynomial.

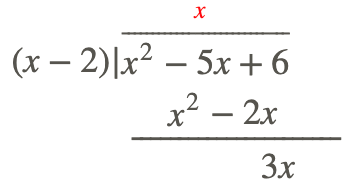
Screen Shot 2021-01-18 at 9.20.54 PM.png

Step 3: Repeat the process until you cannot repeat it anymore.

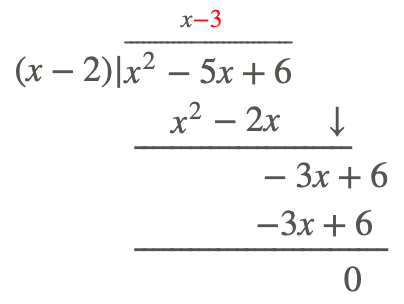
Screen Shot 2021-01-18 at 9.21.37 PM.png

Therefore: \(\ \frac{x^{2}-5 x+6}{x-2}=(x-3)\)

Example 2

Use long division to divide:

\(\ \frac{x^{2}+6 x-7}{x-1}\)

Solution

Step 1: Divide the first term in the numerator by the first term in the denominator, put this in your answer. Therefore \(\ \frac{x^{2}}{x}=x\).

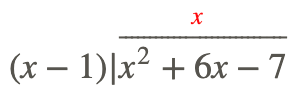
Screen Shot 2021-01-18 at 9.26.30 PM.png

Step 2: Multiply the denominator by this number (variable) and put it below your numerator, subtract and get your new polynomial.

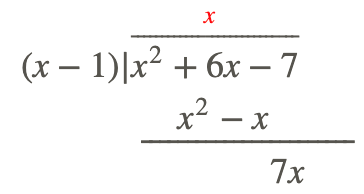
Screen Shot 2021-01-18 at 9.27.12 PM.png

Step 3: Repeat the process until you cannot repeat it anymore.

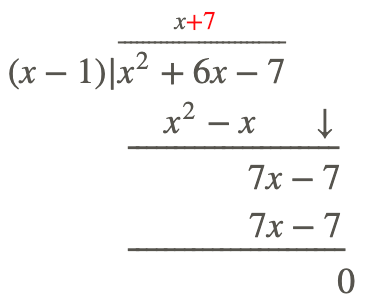
Screen Shot 2021-01-18 at 9.27.46 PM.png

Therefore: \(\ \frac{x^{2}+6 x-7}{x-1}=(x+7)\)

Example 3

Use long division to divide:

\(\ \frac{2 x^{2}+7 x+5}{2 x+5}\)

Solution

Step 1: Divide the first term in the numerator by the first term in the denominator; put this in your answer. Therefore \(\ \frac{2 x^{2}}{2 x}=x\).

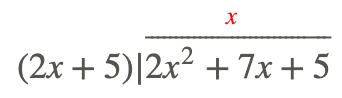
Screen Shot 2021-01-18 at 9.34.32 PM.png

Step 2: Multiply the denominator by this number (variable) and put it below your numerator, subtract and get your new polynomial.

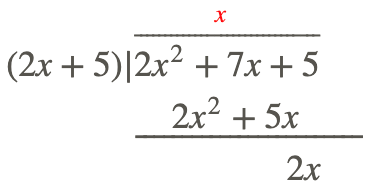
Screen Shot 2021-01-18 at 9.35.36 PM.png

Step 3: Repeat the process until you cannot repeat it anymore.

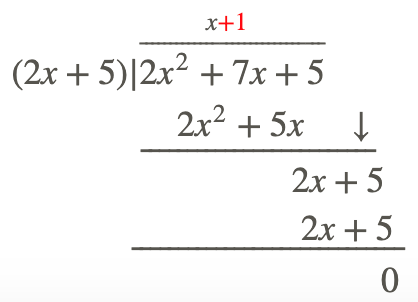
Screen Shot 2021-01-18 at 9.36.33 PM.png

Therefore: \(\ \frac{2 x^{2}+7 x+5}{2 x+5}=(x+1)\)

Example 4

Use synthetic division to divide:

\(\ \frac{3 x^{2}+x-4}{x-1}\)

Solution

Step 1: Write the coefficients in an upside down division sign.

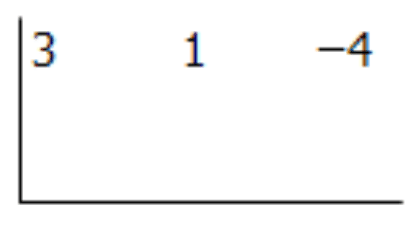
f-d_0ff01d5252c846f566fff615a81cc2c11a113ea7017b82d2f8877970+IMAGE_THUMB_POSTCARD_TINY+IMAGE_THUMB_POSTCARD_TINY.png

Step 2: Put the opposite of the number from the divisor to the left of the division symbol.

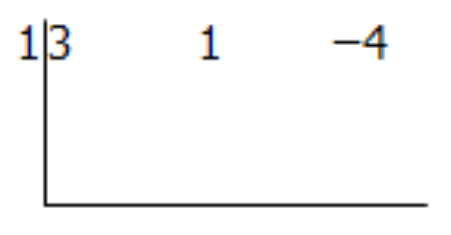
f-d_900e5931238f2ddd61b31077faa64a0b468e00849d921a53de45a8ad+IMAGE_THUMB_POSTCARD_TINY+IMAGE_THUMB_POSTCARD_TINY.png

Step 3: Take your leading coefficient and bring it down below the division symbol.

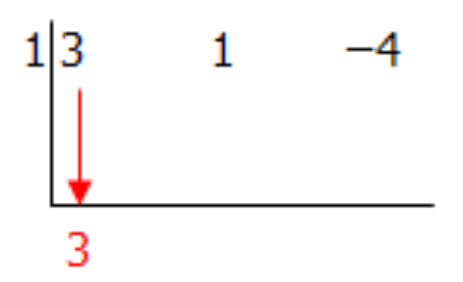
f-d_ee0a2bb1208c88acd667806ffe005fc67b42003027492a3638ff5e4c+IMAGE_THUMB_POSTCARD_TINY+IMAGE_THUMB_POSTCARD_TINY.png

Step 4: Multiply this number by the number to the left of the division symbol and place it in the next column. Add the two numbers together and place this new number below the division sign.

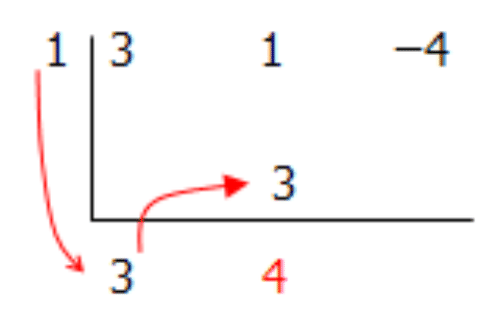
f-d_35902179b39a44c2b1989ff6a361c1905f0bcbede772d08920ec85bc+IMAGE_THUMB_POSTCARD_TINY+IMAGE_THUMB_POSTCARD_TINY.png

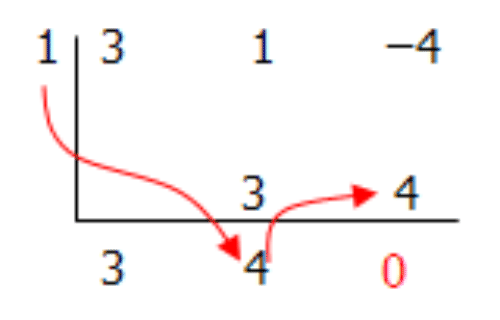
f-d_1eace6276bd4c484cddba64322ebc7d03cd4137310c8ea6992500171+IMAGE_THUMB_POSTCARD_TINY+IMAGE_THUMB_POSTCARD_TINY.png

Therefore: \(\ \frac{3 x^{2}+x-4}{x-1}=(3 x+4)\)

Review

Use long division to divide each of the following:

(x²+7x+12)÷(x+3)
(x²+4x+3)÷(x+3)
(a²−4a−45)÷(a−9)
(3x²+5x−2)÷(3x−1)
(2x²−5x+2)÷(2x−1)

Use synthetic division to divide each of the following:

(b²−5b+6)÷(b−3)
(x²−6x+8)÷(x−4)
(a²−1)÷(a+1)
(c²−9)÷(c−3)
(5r²+2r−3)÷(r+1)

Divide each of the following:

\(\ \frac{2 x^{3}-7 x^{2}-14 x-5}{x-5}\)
\(\ \frac{9 x^{4}-15 x^{3}+12 x^{2}-11 x-15}{3 x^{3}+4 x+3}\)
\(\ \frac{6 x^{4}+4 x^{3}+9 x^{2}+2 x+3}{2 x^{2}+1}\)
\(\ \frac{x^{4}+4 x^{3}+3 x^{2}+x+1}{x+1}\)
\(\ \frac{2 x^{3}+7 x^{2}-27 x+18}{x+6}\)
\(\ \frac{8 x^{3}-2 x^{2}+7 x+5}{2 x+1}\)
\(\ \frac{3 x^{3}-15 x^{2}+4 x-20}{x-5}\)
\(\ \frac{9 x^{3}+26 x^{2}-48 x+5}{x^{2}+3 x-5}\)
\(\ \frac{-x^{3}+13 x+12}{x+3}\)
\(\ \frac{x^{3}-2 x^{2}-5 x+10}{x-2}\)

Review (Answers)

To see the Review answers, open this PDF file and look for section 7.13.

Vocabulary

Term	Definition
Dividend	In a division problem, the dividend is the number or expression that is being divided.
divisor	In a division problem, the divisor is the number or expression that is being divided into the dividend. For example: In the expression 152÷6, 6 is the divisor and 152 is the dividend.

Image Attributions

[Figure 1]
Source: https://commons.wikimedia.org/wiki/File:Computer_in_tuition_centre.JPG
[Figure 2]
Source: https://commons.wikimedia.org/wiki/File:Computer_in_tuition_centre.JPG
[Figure 3]
Source: https://commons.wikimedia.org/wiki/File:Computer_in_tuition_centre.JPG
[Figure 4]
Source: https://commons.wikimedia.org/wiki/File:Computer_in_tuition_centre.JPG
[Figure 5]
Source: https://commons.wikimedia.org/wiki/File:Computer_in_tuition_centre.JPG
[Figure 6]
Source: https://commons.wikimedia.org/wiki/File:Computer_in_tuition_centre.JPG

Search

Text Color

Text Size

Margin Size

Font Type

Example 1

Example 2

Example 3

Example 4