6.1.1: Ellipses Centered at the Origin
- Page ID
- 14747
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ellipses Centered at the Origin
Your homework assignment is to draw the ellipse \(\ 16 x^{2}+4 y^{2}=144\). Where will the foci of your graph be located?
Ellipses Centered at the Origin
The third conic section is an ellipse. Recall that a circle is when a plane sliced through a cone and that plane is parallel to the base of the cone. An ellipse is formed when that plane is not parallel to the base. Therefore, a circle is actually a more specific version of an ellipse.
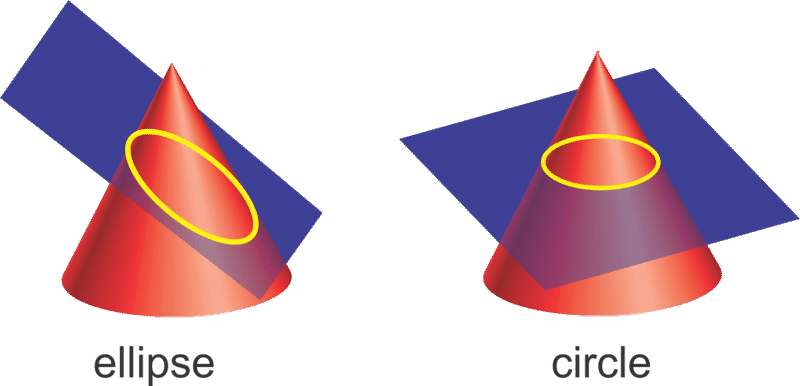
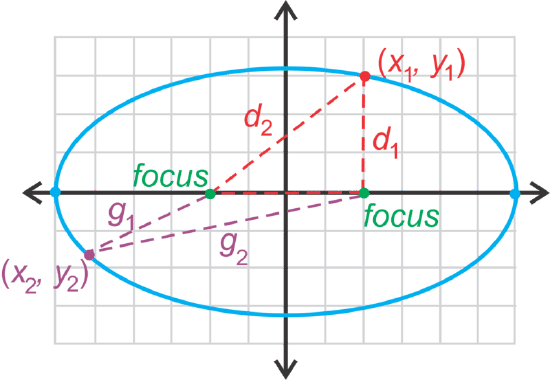
By definition, an ellipse is the set of all points such that the sum of the distances from two fixed points, called foci (the plural of focus), is constant.
Drawing an Ellipse
We will use the definition of an ellipse to draw an ellipse.
Step 1: On a piece of graph paper, draw a set of axes and plot (−2, 0) and (2, 0). These will be the foci.
Step 2: From the definition, we can conclude a point (x, y) is on an ellipse if the sum of the distances is always constant. In the picture, d1 + d2 = r and g1 + g2 = r.
Step 3: Determine how far apart the foci are. Then, find d1 and d2.
Step 4: Determine if the point (−2, 3) is on the ellipse.
In this concept, the center of an ellipse will be (0,0). An ellipse can have either a vertical or horizontal orientation (see below). There are always two foci and they are on the major axis. The major axis is the longer of the two axes that pass through the center of an ellipse. Also on the major axis are the vertices, which its endpoints and are the furthest two points away from each other on an ellipse. The shorter axis that passes through the center is called the minor axis, with endpoints called co-vertices. The midpoint of both axes is the center.
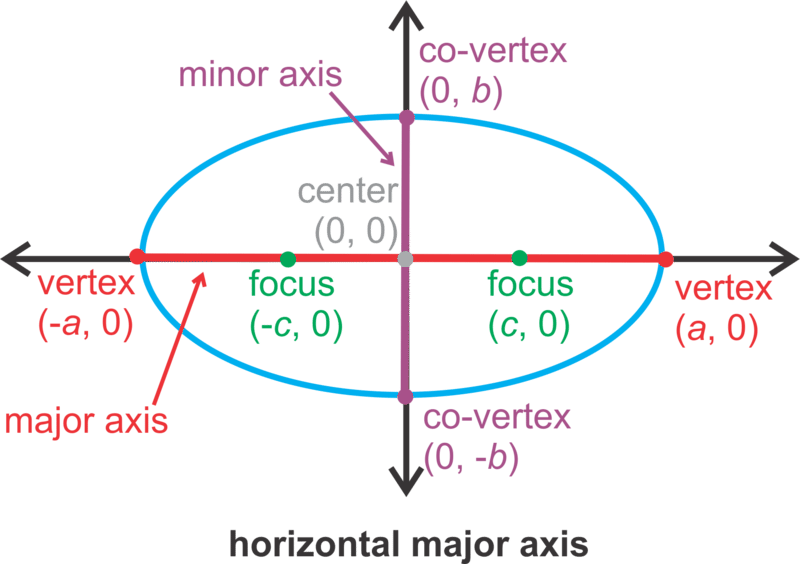
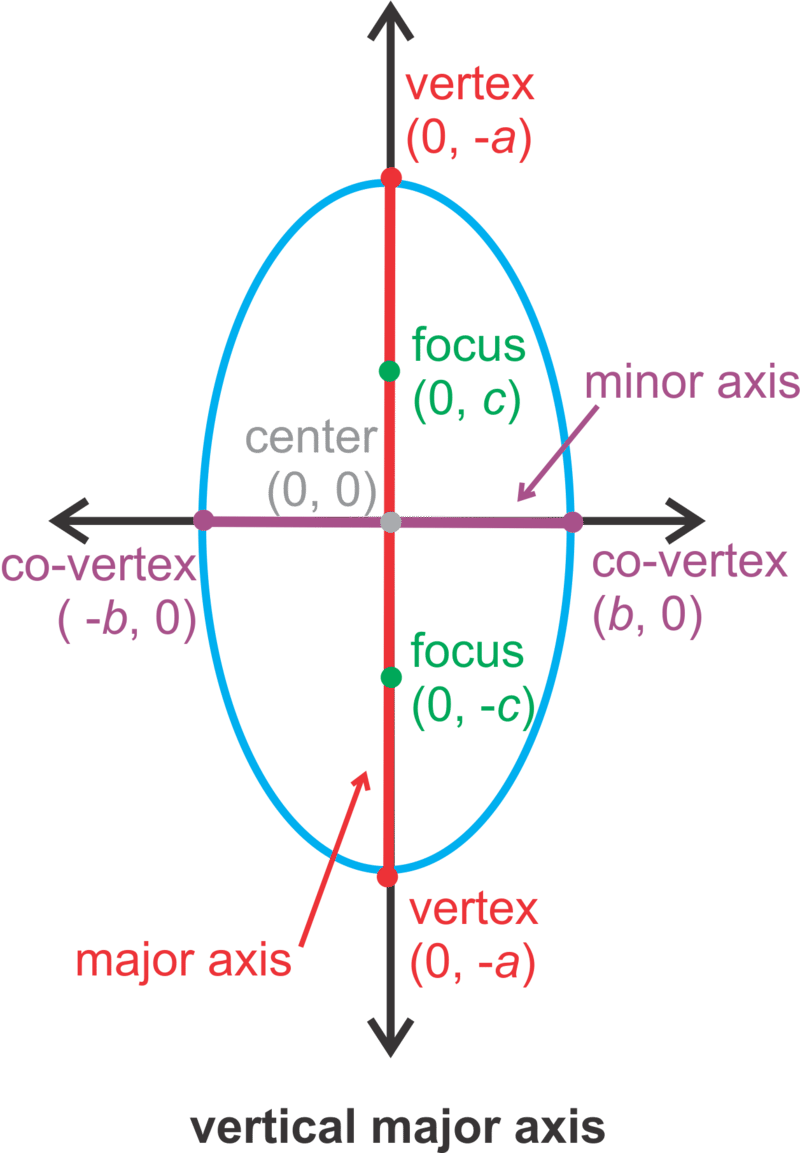
| \(\ \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) |
HORIZONTAL major axis is the x-axis with length 2a. minor axis is the y-axis with length 2b. |
|---|---|
| \(\ \frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}}=1\) |
VERTICAL major axis is the y-axis with length 2a. minor axis is the x-axis with length 2b. |
Other Important Facts
- a is ALWAYS greater than b. If they are equal, we have a circle.
- The foci, vertices, and co-vertices relate through a version of the Pythagorean Theorem: c2 = a2 − b2
Let's find the vertices, co-vertices, and foci of \(\ \frac{x^{2}}{64}+\frac{y^{2}}{25}=1\). Then, let's graph the ellipse.
First, we need to determine if this is a horizontal or vertical ellipse. Because 64 > 25, we know that the ellipse will be horizontal. Therefore, \(\ a^{2}=64\) making \(\ a=\sqrt{64}=8\) and \(\ b^{2}=25\), making \(\ b=\sqrt{25}=5\). Using the pictures above, the vertices will be \(\ (8,0)\) and \(\ (-8,0)\) and the co-vertices will be \(\ (0,5)\) and \(\ (0,−5)\).
To find the foci, we need to use the equation \(\ c^{2}=a^{2}-b^{2}\) and solve for \(\ c\).
\(\ \begin{aligned}
c^{2} &=64-25=39 \\
c &=\sqrt{39}
\end{aligned}\)
The foci are \(\ (\sqrt{39}, 0)\) and \(\ (-\sqrt{39}, 0)\).
To graph the ellipse, plot the vertices and co-vertices and connect the four points to make the closed curve.

Now, let's graph \(\ 49 x^{2}+9 y^{2}=441\) and identify the foci.
This equation is not in standard form. To rewrite it in standard form, the right side of the equation must be 1. Divide everything by 441.
\(\ \begin{aligned}
\frac{49 x^{2}}{441}+\frac{9 y^{2}}{441} &=\frac{441}{441} \\
\frac{x^{2}}{9}+\frac{y^{2}}{49} &=1
\end{aligned}\)
Now, we can see that this is a vertical ellipse, where \(\ b=3\) and \(\ a=7\).

To find the foci, use \(\ c^{2}=a^{2}-b^{2}\).
\(\ \begin{array}{c}
c^{2}=49-9=40 \\
c=\sqrt{40}=2 \sqrt{10}
\end{array}\)
The foci are \(\ (0,2 \sqrt{10})\) and \(\ (0,-2 \sqrt{10})\).
Finally, let's write equations for the ellipses with the given characteristics below and centered at the origin.
In either part, you may wish to draw the ellipse to help with the orientation.
- vertex: (−6, 0), co-vertex: (0, 4)
We can conclude that \(\ a=6\) and \(\ b=4\). The ellipse is horizontal, because the larger value, \(\ a\), is the x-value of the vertex. The equation is \(\ \frac{x^{2}}{36}+\frac{y^{2}}{16}=1\).
- vertex: (0, 9), focus: (0, −5)
We know that \(\ a=9\) and \(\ c=5\) and that the ellipse is vertical. Solve for \(\ b\) using \(\ c^{2}=a^{2}-b^{2}\)
\(\ \begin{array}{l}
5^{2}=9^{2}-b^{2} \\
25=81-b^{2} \\
b^{2}=56 \rightarrow b=2 \sqrt{14}
\end{array}\)The equation is \(\ \frac{x^{2}}{56}+\frac{y^{2}}{81}=1\)
Examples
Earlier, you were asked to determine where the foci of your graph would be located.
Solution
This equation is not in standard form. To rewrite it in standard form, the right side of the equation must be 1. Divide everything by 144.
\(\ \begin{aligned}
\frac{16 x^{2}}{144}+\frac{4 y^{2}}{144} &=\frac{144}{144} \\
\frac{x^{2}}{9}+\frac{y^{2}}{36} &=1
\end{aligned}\)
Now, we can see that this is a vertical ellipse, where \(\ b=3\) and \(\ a=6\).
To find the foci, use \(\ c^{2}=a^{2}-b^{2}\).
\(\ \begin{aligned}
c^{2} &=36-9=27 \\
c &=\sqrt{27}=3 \sqrt{3}
\end{aligned}\)
The foci are therefore \(\ (0,3 \sqrt{3})\) and \(\ (0,-3 \sqrt{3})\).
Find the vertices, co-vertices, and foci of \(\ \frac{x^{2}}{4}+\frac{y^{2}}{36}=1\). Then, graph the equation.
Solution
Because the larger number is under \(\ y^{2}\), the ellipse is vertical. Therefore, \(\ a=6\) and \(\ b^{2}\). Use \(\ c^{2}=a^{2}-b^{2}\) to find \(\ c\).
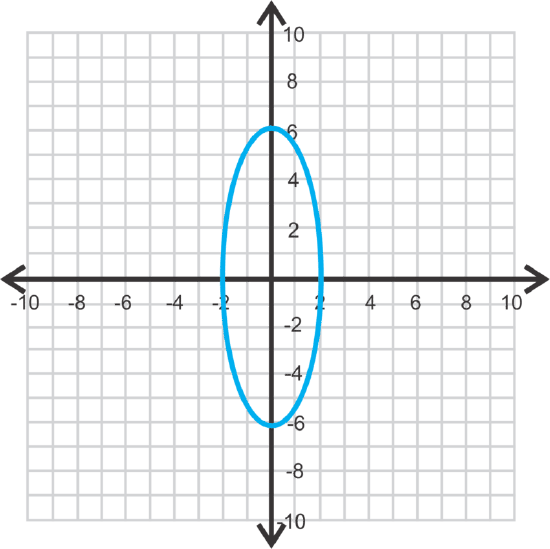
\(\ \begin{array}{c}
c^{2}=6^{2}-2^{2}=36-4=32 \\
c=\sqrt{32}=4 \sqrt{2}
\end{array}\)
vertices: \(\ (0,6)\) and \(\ (0,−6)\)
co-vertices: \(\ (2,0)\) and \(\ (−2,0)\)
foci: \(\ (0,4 \sqrt{2})\) and \(\ (0,-4 \sqrt{2})\)
Graph \(\ 49 x^{2}+64 y^{2}=3136\) and find the foci.
Solution
Rewrite \(\ 49 x^{2}+64 y^{2}=3136\) in standard form.
\(\ \begin{aligned}
\frac{49 x^{2}}{3136}+\frac{64 y^{2}}{3136} &=\frac{3136}{3136} \\
\frac{x^{2}}{64}+\frac{y^{2}}{49} &=1
\end{aligned}\)

This ellipse is horizontal with \(\ a=8\) and \(\ b=7\). Find \(\ c\).
\(\ \begin{aligned}
c^{2} &=64-49=15 \\
c &=\sqrt{15}
\end{aligned}\)
The foci are \(\ (-\sqrt{15}, 0)\) and \(\ (\sqrt{15}, 0)\).
Find the equation of the ellipse with co-vertex \(\ (0,−7)\), focus \(\ (15,0)\) and centered at the origin.
Solution
Because the co-vertex is \(\ (0,−7)\), \(\ b=7\) and the ellipse is horizontal. From the foci, we know that \(\ c=15\). Find \(\ a\).
\(\ \begin{aligned}15^{2}&=a^{2}-7^{2}\\
a^{2}&=225+49=274 \quad \quad\quad\text{The equation is } \frac{x^{2}}{274}+\frac{y^{2}}{49}=1\\
a&=\sqrt{274} \end{aligned}\)
Review
Find the vertices, co-vertices, and foci of each ellipse below. Then, graph.
- \(\ \frac{x^{2}}{9}+\frac{y^{2}}{16}=1\)
- \(\ 4 x^{2}+25 y^{2}=100\)
- \(\ \frac{x^{2}}{64}+y^{2}=1\)
- \(\ 81 x^{2}+100 y^{2}=8100\)
- \(\ \frac{x^{2}}{49}+\frac{y^{2}}{16}=1\)
- \(\ 121 x^{2}+9 y^{2}=1089\)
Find the equation of the ellipse, centered at the origin, with the given information.
- vertex: (−3, 0) co-vertex: (0, 1)
- co-vertex: (7, 0) major axis: 18 units
- vertex: (0, 5) minor axis: 4 units
- vertex: (0, 6) co-vertex: (−2, 0)
- co-vertex: (17, 0) focus: (0, 17)
- vertex: (4, 0) focus: (−3, 0)
- co-vertex: (−6, 0) focus: (0, 5)
- focus: (0, −9) minor axis: 16 units
- Real Life Application A portion of the backyard of the White House is called The Ellipse. The major axis is 1058 feet and the minor axis is 903 feet. Find the equation of the horizontal ellipse, assuming it is centered at the origin.

Answers for Review Problems
To see the Review answers, open this PDF file and look for section 10.5.
Vocabulary
| Term | Definition |
|---|---|
| Equation of an Ellipse | If the center of an ellipse is (0, 0), the equation of the ellipse is of the form \(\ \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) or \(\ \frac{y^{2}}{a^{2}}+\frac{x^{2}}{b^{2}}=1\). |
| Major Axis | The major axis of an ellipse is the longest diameter of the ellipse. |
Image Attributions
- [Figure 1]
Credit: Ad Meskens
Source: https://commons.wikimedia.org/wiki/File:Illu_pancrease.jpg;https://commons.wikimedia.org/wiki/File:President%27s_Park_with_White_House.jpg

