6.2.3: Parabolas with any Vertex
- Page ID
- 14754
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Parabolas with Vertex at (h, k)
Your homework assignment is to find the focus of the parabola \(\ (x+4)^{2}=-12(y-5)\). You say the focus is (−4, 5). Banu says the focus is (0, −3). Carlos says the focus is (−4, 2). Which one of you is correct?
Parabolas with Vertex at (h, k)
You have already learned that parabolas don’t always have their vertex at (0, 0). In this concept, we will address parabolas where the vertex is (h, k), learn how to find the focus, directrix and graph.
Recall that the equation of a parabola is \(\ x^{2}=4 p y\) or \(\ y^{2}=4 p x\) and the vertex is on the origin. Also, recall that the vertex form of a parabola is \(\ y=a(x-h)^{2}+k\). Combining the two, we can find the vertex form for conics.
\(\ \begin{aligned}
y &=a(x-h)^{2}+k \text { and } x^{2}=4 p y & & \text { Solve the first for }(x-h)^{2} \\
(x-h)^{2} &=\frac{1}{a}(y-k) & & \text { We found that } 4 p=\frac{1}{a} \\
(x-h)^{2} &=4 p(y-k) & &
\end{aligned}\)
If the parabola is horizontal, then the equation will be \(\ (y-k)^{2}=4 p(x-h)\). Notice, that even though the orientation is changed, the \(\ h\) and \(\ k\) values remain with the \(\ x\) and \(\ y\) values, respectively.
Finding the focus and directrix are a little more complicated. Use the extended table below to help you find these values.
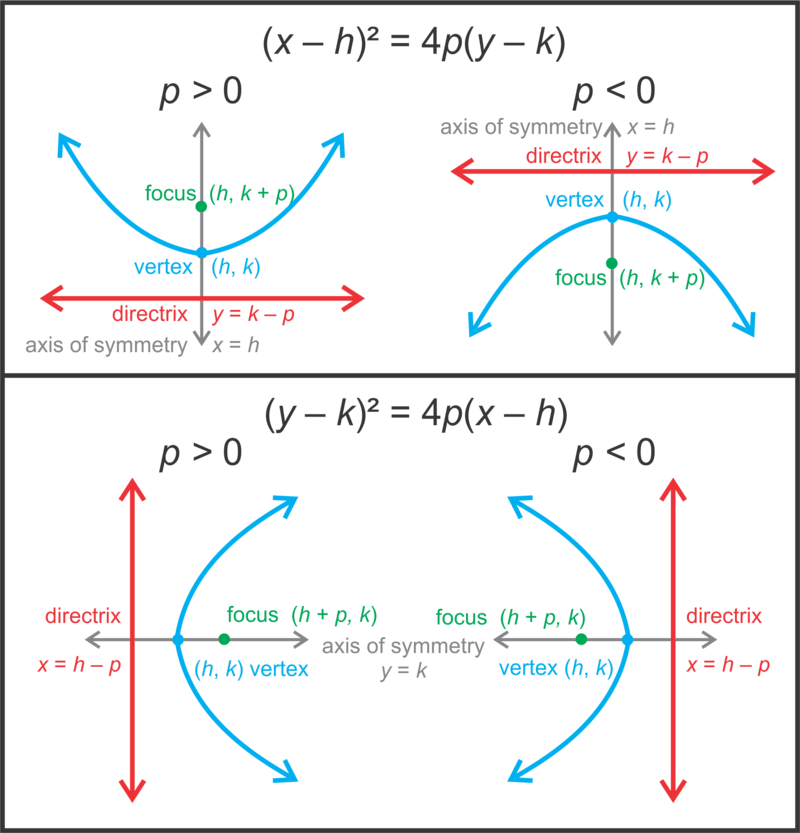
Notice that the way we find the focus and directrix does not change whether \(\ p\) is positive or negative.
Let's analyze the equation \(\ (y-1)^{2}=8(x+3)\). We'll find the vertex, axis of symmetry, focus, and directrix. Then, we'll determine if the function opens up, down, left or right.
First, because \(\ y\) is squared, we know that the parabola will open to the left or right. We can conclude that the parabola will open to the right because 8 is positive, meaning that \(\ p\) is positive. Next, find the vertex. Using the general equation, \(\ (y-k)^{2}=4 p(x-h)\), the vertex is (−3, 1) and the axis of symmetry is \(\ y=1\). Setting \(\ 4 p=8\), we have that \(\ p=2\). Adding \(\ p\) to the \(\ x\)-value of the vertex, we get the focus, (−1, 1). Subtracting \(\ p\) from the \(\ x\)-value of the vertex, we get the directrix, \(\ x=−5\).
Let's graph the parabola from the problem above. Plot the vertex, axis of symmetry, focus, and directrix.
First, plot all the critical values we found earlier. Then, determine a set of symmetrical points that are on the parabola to make sure your curve is correct. If \(\ x=5\), then \(\ y\) is either -7 or 9. This means that the points (5, −7) and (5, 9) are both on the parabola.
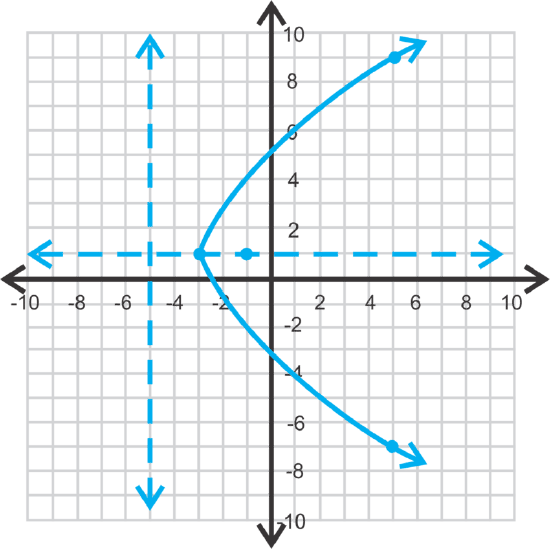
It is important to note that parabolas with a horizontal orientation are not functions because they do not pass the vertical line test.
The vertex of a parabola is (−2, 4) and the directrix is y=7. Let's find the equation of the parabola.
First, let’s determine the orientation of this parabola. Because the directrix is horizontal, we know that the parabola will open up or down (see table/pictures above). We also know that the directrix is above the vertex, making the parabola open down and \(\ p\) will be negative (plot this on an x−y plane if you are unsure).
To find \(\ p\), we can use the vertex, \(\ (h,k)\) and the equation for a horizontal directrix, \(\ y=k−p\).
\(\ \begin{aligned}
7 &=4-p \\
3 &=-p \quad\quad\quad\quad \text{Remember, } p \text{ is negative because of the downward orientation of the parabola.}\\
-3 &=p
\end{aligned}\)
Now, using the general form, \(\ (x-h)^{2}=4 p(y-k)\), we can find the equation of this parabola.
\(\ \begin{aligned}
(x-(-2))^{2} &=4(-3)(y-4) \\
(x+2)^{2} &=-12(y-4)
\end{aligned}\)
Examples
Earlier, you were asked to determine which student is correct.
Solution
This parabola is of the form \(\ (x-h)^{2}=4 p(y-k)\). From the table earlier in this lesson, we can see that the focus of a parabola of this form is \(\ (h, k+p)\). So now we have to find h, k, and p.
If we compare \(\ (x+4)^{2}=-12(y-5)\) to \(\ (x-h)^{2}=4 p(y-k)\), we see that:
- \(\ 4=-h \text { or } h=-4\)
- \(\ -12=4 p \text { or } p=-3\)
- \(\ 5=k\)
From these facts we can find \(\ k+p=5+(-3)=2\).
Therefore, the focus of the parabola is \(\ (−4,2)\) and Carlos is correct.
Find the vertex, focus, axis of symmetry and directrix of \(\ (x+5)^{2}=2(y+2)\).
Solution
The vertex is \(\ (-5,-2)\) and the parabola opens up because \(\ p\) is positive and \(\ x\) is squared.
\(\ 4 p=2\), making \(\ p=\frac{1}{2}\). The focus is \(\ (-5,-2+2)\) or \(\ (-5,0)\), the axis of symmetry is \(\ x=-5\), and the directrix is \(\ y=-2-\frac{1}{2}\) or \(\ y=-2 \frac{1}{2}\).
Graph the parabola from Example 2.
Solution
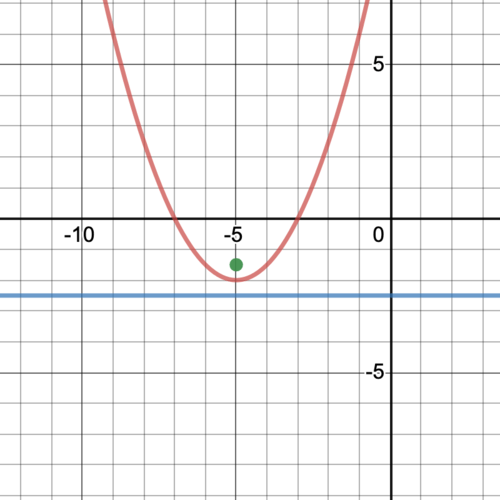
Find the equation of the parabola with vertex (−5, −1) and focus (−8, −1).
Solution
The vertex is (−5, −1), so \(\ h=−5\) and \(\ k=−1\). The focus is (−8, −1), meaning that that parabola will be horizontal. We know this because the y-values of the vertex and focus are both -1. Therefore, \(\ p\) is added or subtracted to \(\ h\).
\(\ (h+p, k) \rightarrow(-8,-1)\) we can infer that \(\ h+p=-8 \rightarrow-5+p=-8\) and \(\ p=-3\)
Therefore, the equation is \(\ (y-(-1))^{2}=4(-3)(x-(-5)) \rightarrow(y+1)^{2}=-12(x+5)\)
Review
Find the vertex, focus, axis of symmetry, and directrix of the parabolas below.
- \(\ (x+1)^{2}=-3(y-6)\)
- \(\ (x-3)^{2}=y-7\)
- \(\ (y+2)^{2}=8(x+1)\)
- \(\ y^{2}=-10(x-3)\)
- \(\ (x+6)^{2}=4(y+8)\)
- \(\ (y-5)^{2}=-\frac{1}{2} x\)
- Graph the parabola from #1.
- Graph the parabola from #2.
- Graph the parabola from #4.
- Graph the parabola from #5.
Find the equation of the parabola given the vertex and either the focus or directrix.
- vertex: (2, −1), focus: (2, −4)
- vertex: (−3, 6), directrix: x = 2
- vertex: (6, 10), directrix: y = 9.5
- Challenge focus: (−1, −2), directrix: x = 3
- Extension Rewrite the equation of the parabola, x2 − 8x + 2y + 22 = 0, in standard form by completing the square. Then, find the vertex.
Answers for Review Problems
To see the Review answers, open this PDF file and look for section 10.2.
Vocabulary
| Term | Definition |
|---|---|
| Vertex form | The vertex form of a parabola is \(\ (x-h)^{2}=4 p(y-k)\) or \(\ (y-k)^{2}=4 p(x-h)\) where \(\ (h,k)\) is the vertex. |
Image Attributions
- [Figure 1]
Credit: Holly Fischer
Source: https://commons.wikimedia.org/wiki/File:Three_Main_Layers_of_the_Eye.png

