6.3.1: Graphs of Hyperbolas Centered at the Origin
- Page ID
- 14758
Graphing Hyperbolas Centered at the Origin
Your homework assignment is to graph the hyperbola \(\ 9 y^{2}-4 x^{2}=36\). What are the asymptotes and foci of your graph?
Graphing Hyperbolas
We know that the resulting graph of a rational function is a hyperbola with two branches. A hyperbola is also a conic section. To create a hyperbola, you would slice a plane through two inverted cones, such that the plane is perpendicular to the bases of the cones.

By the conic definition, a hyperbola is the set of all points such that the of the differences of the distances from the foci is constant.
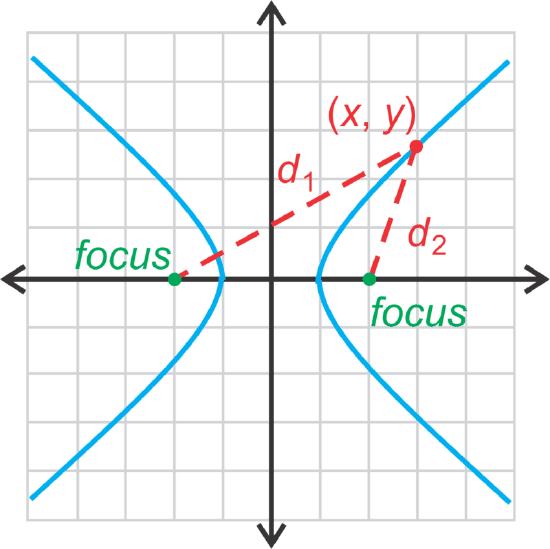
Using the picture, any point, \(\ (x,y)\) on a hyperbola has the property, \(\ d_{1}-d_{2}=P\), where \(\ P\) is a constant.
Comparing this to the ellipse, where \(\ d_{1}+d_{2}=P\) and the equation was \(\ \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) or \(\ \frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}}=1\).
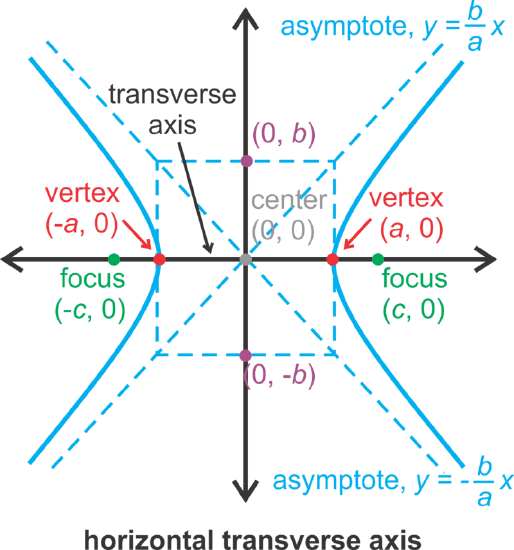
For a hyperbola, then, the equation will be \(\ \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) or \(\ \frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\). Notice in the vertical orientation of a hyperbola, the \(\ y^{2}\) term is first. Just like with an ellipse, there are two vertices, on the hyperbola. Here, they are the two points that are closest to each other on the graph. The line through the vertices and foci is called the transverse axis. Its midpoint is the center of the hyperbola. In this concept, the center will be the origin. There will always be two branches for any hyperbola and two asymptotes.

Let's graph \(\ \frac{x^{2}}{64}-\frac{y^{2}}{25}=1\) and then find the vertices, foci, and asymptotes.
First, this hyperbola has a horizontal transverse axis because the \(\ x^{2}\) term is first. Also, with hyperbolas, the \(\ a\) and \(\ b\) term stay in place, but the \(\ x\) and \(\ y\) terms switch. \(\ a\) is not always greater than \(\ b\).
Therefore, \(\ a=\sqrt{64}=8\) and \(\ b=\sqrt{25}=5\). To graph this hyperbola, go out 8 units to the left and right of the center and 5 units up and down to make a rectangle. The diagonals of this rectangle are the asymptotes.
Draw the hyperbola branches with the vertices on the transverse axis and the rectangle. Sketch the branches to get close to the asymptotes, but not touch them.
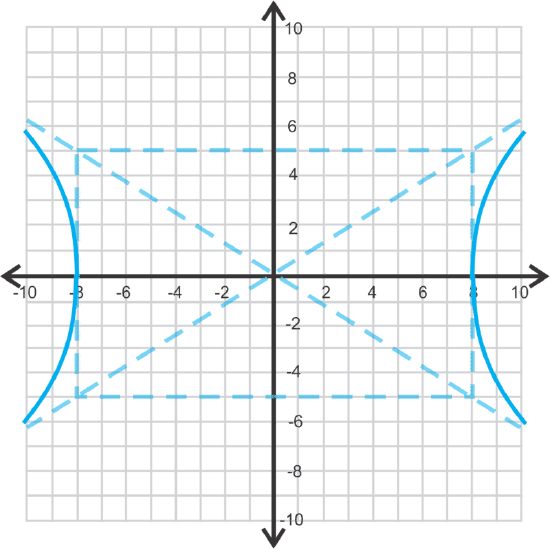
The vertices are \(\ (\pm 8,0)\) and the asymptotes are \(\ y=\pm \frac{5}{8} x\) (see pictures above. To find the foci, we use the Pythagorean Theorem, \(\ c^{2}=a^{2}+b^{2}\) because the foci are further away from the center than the vertices.
\(\ \begin{aligned}
c^{2} &=64+25=89 \\
c &=\sqrt{89}
\end{aligned}\)
The foci are \(\ (\pm \sqrt{89}, 0)\).
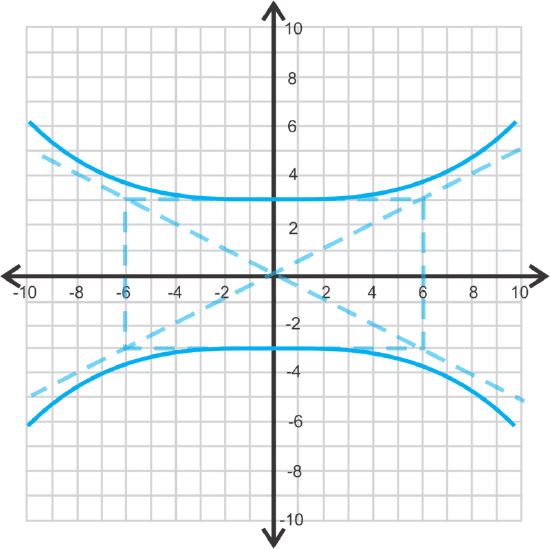
Now, let's graph \(\ 36 y^{2}-9 x^{2}=324\) and identify the foci.
This equation is not in standard form. To rewrite it in standard form, the right side of the equation must be 1. Divide everything by 324.
\(\ \begin{aligned}
\frac{36 y^{2}}{324}-\frac{9 x^{2}}{324} &=\frac{324}{324} \\
\frac{y^{2}}{9}-\frac{x^{2}}{36} &=1
\end{aligned}\)
Now, we can see that this is a vertical hyperbola, where \(\ a=3\) and \(\ b=6\). Draw the rectangle, asymptotes, and plot the vertices on the \(\ y \text { -axis }\).
To find the foci, use \(\ c^{2}=a^{2}+b^{2}\).
\(\ \begin{array}{l}
c^{2}&=36+9=45 \\
c&=\sqrt{45}=3 \sqrt{5}
\end{array}\)
The foci are \(\ (0,3 \sqrt{5})\) and \(\ (0,-3 \sqrt{5})\)
Finally, let's graph \(\ \frac{x^{2}}{4}-\frac{y^{2}}{4}=1\) and identify the asymptotes.
This will be a horizontal hyperbola, because the \(\ x \text { -term }\) is first. \(\ a\) and \(\ b\) will both be 2 because \(\ \sqrt{4}=2\). Draw the square and diagonals to form the asymptotes.
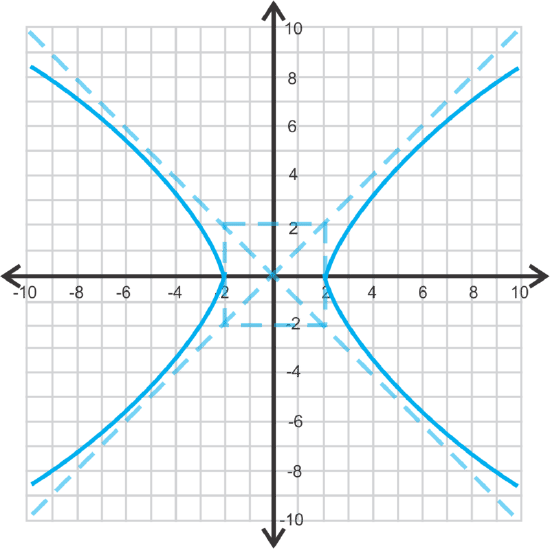
The asymptotes are \(\ y=\pm \frac{2}{2} x\) or \(\ y=x\) and \(\ y=-x\).
Important Note: The asymptotes and square are not a part of the function. They are included in graphing a hyperbola because it makes it easier to do so.
Also, when graphing hyperbolas, we are sketching each branch. We did not make a table of values to find certain points and then connect. You can do this, but using the square or rectangle with the asymptotes produces a pretty accurate graph and is much simpler.
Examples
Earlier, you were asked to find the asymptotes and foci of your graph.
Solution
First, we need to get the equation in the form \(\ \frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\), so divide by 36.
\(\ \begin{array}{l}
9 y^{2}-4 x^{2}&=36 \\
\frac{9 y^{2}}{36}-\frac{4 x^{2}}{36}&=\frac{36}{36} \\
\frac{y^{2}}{4}-\frac{x^{2}}{9}&=1
\end{array}\)
Now we can see that \(\ a^{2}=4\) and \(\ b^{2}=9\), so \(\ a=2\) and \(\ b=3\). Also, because the \(\ y \text { -term }\) comes first, the hyperbola is vertically oriented. Therefore, the asymptotes are \(\ y=-\frac{a}{b} x\) and \(\ y=\frac{a}{b} x\).
Substituting for \(\ a\) and \(\ b\), we get \(\ y=-\frac{2}{3} x\) and \(\ y=\frac{2}{3} x\).
Finally, to find the foci, use \(\ c^{2}=a^{2}+b^{2}\).
\(\ \begin{array}{l}
c^{2}&=4+9=13 \\
c&=\sqrt{13}
\end{array}\)
The foci are \(\ (0, \sqrt{13})\) and \(\ (0,-\sqrt{13})\).
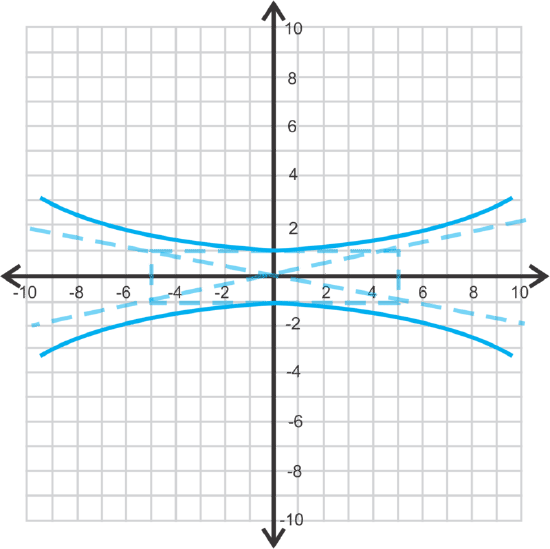
Find the vertices, foci, and asymptotes of \(\ y^{2}-\frac{x^{2}}{25}=1\).
Solution
First, let’s rewrite the equation like this: \(\ \frac{y^{2}}{1}-\frac{x^{2}}{25}=1\). We know that the transverse axis is vertical because the \(\ y \text { -term }\) is first, making \(\ a=1\) and \(\ b=5\). Therefore, the vertices are \(\ (0,−1)\) and \(\ (0,1)\). The asymptotes are \(\ y=\frac{1}{5} x\) and \(\ y=-\frac{1}{5} x\). Lastly, let’s find the foci using \(\ c^{2}=a^{2}+b^{2}\).
\(\ \begin{array}{l}
c^{2}&=1+25=26 \\
c&=\sqrt{26}
\end{array}\)
The foci are \(\ (0,-\sqrt{26})\) and \(\ (0, \sqrt{26})\)
Graph Example 2.
Solution
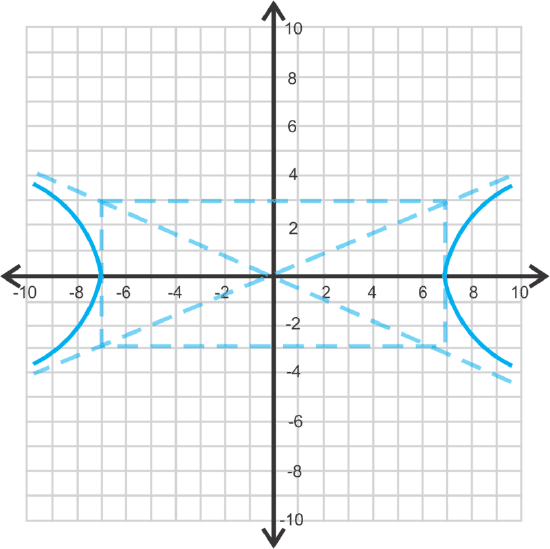
Graph \(\ 9 x^{2}-49 y^{2}=411\).
Solution
Rewrite the equation so that the right side is equal to 1. Divide everything by 441.
\(\ \begin{aligned}
\frac{9 x^{2}}{441}-\frac{49 y^{2}}{441} &=\frac{441}{441} \\
\frac{x^{2}}{49}-\frac{y^{2}}{9} &=1
\end{aligned}\)
\(\ a=9\) and \(\ b=6\) with a horizontal transverse axis.
Review
Find the vertices, asymptotes, and foci of each hyperbola below.
- \(\ \frac{x^{2}}{9}-\frac{y^{2}}{16}=1\)
- \(\ 4 y^{2}-25 x^{2}=100\)
- \(\ \frac{x^{2}}{81}-\frac{y^{2}}{64}=1\)
- \(\ x^{2}-y^{2}=16\)
- \(\ \frac{y^{2}}{49}-\frac{x^{2}}{25}=1\)
- \(\ 121 y^{2}-9 x^{2}=1089\)
- \(\ y^{2}-x^{2}=1\)
- \(\ \frac{x^{2}}{64}-\frac{y^{2}}{4}=1\)
- \(\ \frac{y^{2}}{4}-\frac{x^{2}}{64}=1\)
- Graph #1.
- Graph #2.
- Graph #8.
- Graph #9.
- Writing Compare the hyperbolas from #8 and #9. How are they the same? How are they different? What do you know about the asymptotes and foci?
- Critical Thinking Compare the equations \(\ \frac{x^{2}}{25}-\frac{y^{2}}{9}=1\) and \(\ \frac{x^{2}}{25}+\frac{y^{2}}{9}=1\). Graph them on the same axes and find their foci.
Answers for Review Problems
To see the Review answers, open this PDF file and look for section 10.7.
Image Attributions
- [Figure 1]
Credit: Image copyright DVARG, 2014, modified by CK-12 Foundation;CK-12 Foundation
Source: http://www.shutterstock.com
License: License from Shutterstock; CC BY-SA

