8.1.3: Infinite Limits
- Page ID
- 14813
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Infinite Limits
Geeks-R-Us sells titanium mechanical pencils to computer algorithm designers. In an effort to attract more business, they decide to run a rather unusual promotion:
"SALE!! The more you buy, the more you save! Pencils are now \(\ \$ \frac{12 x}{x-3}\) per dozen!"
If the trillionaire, Spug Dense, comes in and says he wants to buy as many pencils as Geeks-R-Us can turn out, what will the cost of the pencils approach as the order gets bigger and bigger?
Infinite Limits
Sometimes, a function may not be defined at a particular number, but as values are input closer and closer to the undefined number, a limit on the output may not exist. For example, for the function f(x) = 1/x (shown in the figures below), as x values are taken closer and closer to 0 from the right, the function increases indefinitely. Also, as x values are taken closer and closer to 0 from the left, the function decreases indefinitely.
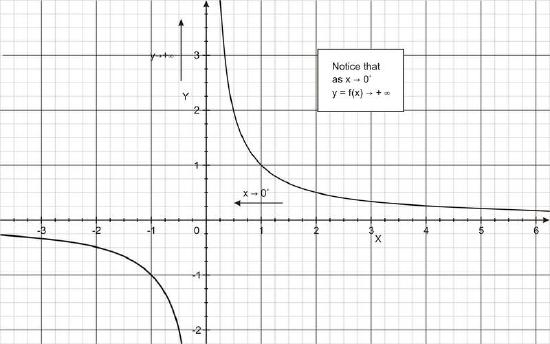
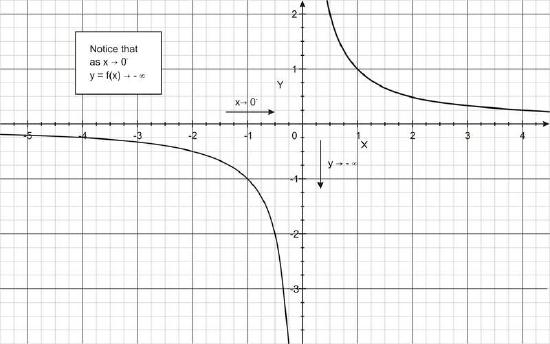
We describe these limiting behaviors by writing
\(\ \begin{array}{l}
\lim _{x \rightarrow 0^{+}} \frac{1}{x}=+\infty \\
\lim _{x \rightarrow 0^{-}} \frac{1}{x}=-\infty
\end{array}\)
Sometimes we want to know the behavior of \(\ f(x)\) as x increases or decreases without bound. In this case we are interested in the end behavior of the function, a concept you have likely explored before. For example, what is the value of \(\ f(x)=1 / x\) as \(\ x\) increases or decreases without bound? That is,
\(\ \begin{array}{l}
\lim _{x \rightarrow+\infty} \frac{1}{x}=? \\
\lim _{x \rightarrow-\infty} \frac{1}{x}=?
\end{array}\)
As you can see from the graphs (shown below), as \(\ x\) decreases without bound, the values of \(\ f(x) = 1/x\) are negative and get closer and closer to 0. On the other hand, as \(\ x\) increases without bound, the values of \(\ f(x) = 1/x\) are positive and still get closer and closer to 0.
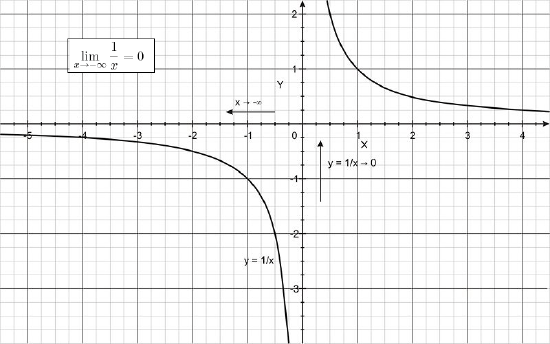
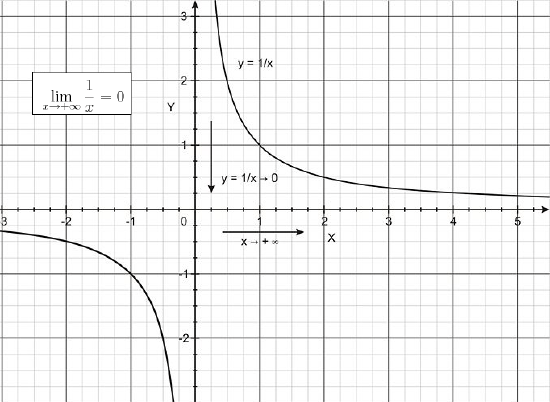
That is,
\(\ \begin{array}{l}
\lim _{x \rightarrow+\infty} \frac{1}{x}=0 \\
\lim _{x \rightarrow-\infty} \frac{1}{x}=0
\end{array}\)
Examples
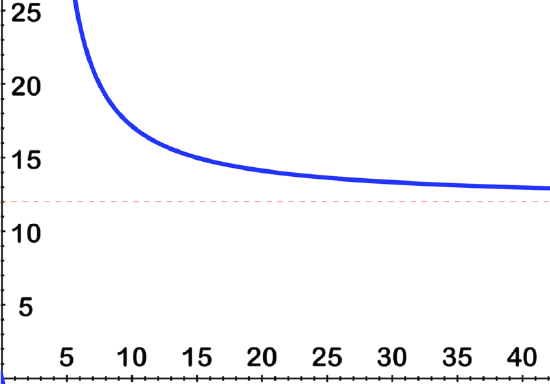
Earlier, you were asked a question about buying a lot of pencils.
Solution
As Spug buys more and more pencils, the cost of each dozen will drop quickly at first, and level out after a while, approaching $12 per dozen.
You can see the effect on the graph here:
Evaluate the limit by making a graph: \(\ \lim _{x \rightarrow 3^{+}} \frac{x+6}{x-3}\)
Solution
By looking at the graph:
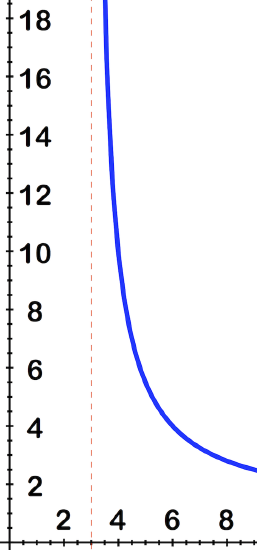
We can see that as x gets closer and closer to 3 from the positive side, the output increases right out the top of the image, on its way to ∞
Evaluate the limit: \(\ \lim _{x \rightarrow \infty} \frac{11 x^{3}-14 x^{2}+8 x+16}{9 x-3}\).
Solution
To evaluate polynomial function limits, a little bit of intuition helps. Let's think this one through.
First, note that since we are looking at what happens as \(\ x \rightarrow \infty\) most of the interesting stuff will happen as \(\ x\) gets really big.
On the top part of the fraction, as x gets truly massive, the \(\ 11 x^{3}\) part will get bigger much faster than either of the other terms. In fact, it increases so much faster than the other terms completely cease to matter at all once x gets really monstrous. That means that the important part of the top of the fraction is just the \(\ 11 x^{3}\).
On the bottom, a similar situation develops. As x gets really, really big, the -3 matters less and less. So the bottom may as well be just \(\ 9x\).
That gives us \(\ \frac{11 x^{3}}{9 x}\) which reduces to \(\ \frac{11 x^{2}}{9}\)
Now we can more easily see what happens at the "ends." As x gets bigger and bigger, the numerator continues to get bigger faster than the denominator, so the overall output also increases.
\(\ \therefore \lim _{x \rightarrow+\infty} \frac{11 x^{3}-14 x^{2}+8 x+16}{9 x-3} \text { is }+\infty\)
Evaluate \(\ \lim _{x \rightarrow 0} \frac{x+2}{x+3}\)
Solution
This one is easier than it looks! As x-->0, leaving just the fraction: 2/3
Make a graph to evaluate the limit \(\ \lim _{x \rightarrow \infty} \frac{1}{\sqrt{x}}\) and \(\ \lim _{x \rightarrow 0^{+}} \frac{1}{\sqrt{x}}\).
Solution
By looking at the image, we see that as x gets huge, so does \(\ \sqrt{x}\) which means that 1 is being divided by an ever-larger number, and the result is getting smaller and smaller.
\(\ \lim _{x \rightarrow \infty} \frac{1}{\sqrt{x}}=0\)
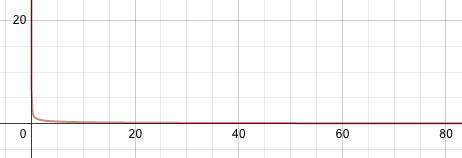
On the same image, we can see that as \(\ x\) gets closer and closer to zero, so does \(\ \sqrt{x}\) which means that 1 is being divided by an ever smaller number, and the result gets bigger and bigger.
\(\ \lim _{x \rightarrow 0^{+}} \frac{1}{\sqrt{x}} \text { is }+\infty\)
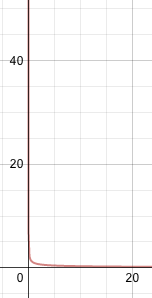
Graph and evaluate the limit: \(\ \lim _{x \rightarrow 2^{+}} \frac{1}{x-2}\).
Solution
By looking at the image, we can see that as x gets closer and closer to 2 from the positive direction, 1 gets divided by smaller and smaller numbers, so the result gets larger and larger.
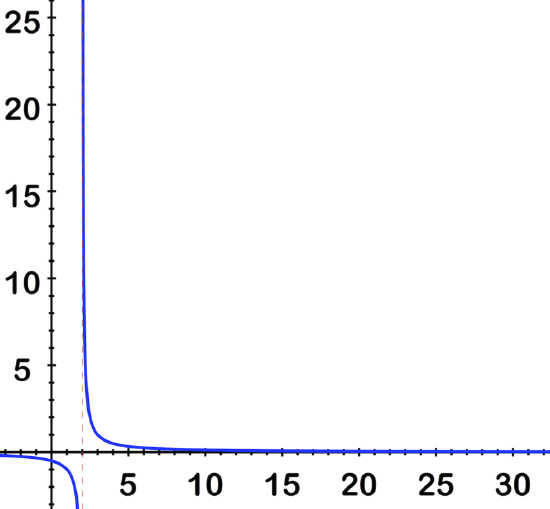
\(\ \lim _{x \rightarrow 2^{+}} \frac{1}{x-2} \text { is }+\infty\)
Review
Evaluate the limits:
- \(\ \lim _{x \rightarrow 3^{-}} \frac{1}{x-3}\)
- \(\ \lim _{x \rightarrow-4^{+}} \frac{1}{x+4}\)
- \(\ \lim _{x \rightarrow-\left(\frac{8}{3}\right)^{+}} \frac{1}{3 x+8}\)
- \(\ \lim _{x \rightarrow-5^{+}} \frac{\left(x^{2}+11 x+30\right)}{x+5}\)
- \(\ \lim _{x \rightarrow-\infty} \frac{\left(x^{2}+11 x+30\right)}{x+5}\)
- \(\ \lim _{x \rightarrow \infty} \frac{-11 x^{3}+20 x^{2}+15 x-17}{-9 x^{3}+5 x^{2}-x-17}\)
- \(\ \lim _{x \rightarrow \infty} 13\)
- \(\ \lim _{x \rightarrow \infty} \frac{-2 x+18}{17 x-3}\)
- \(\ \lim _{x \rightarrow \infty} 15\)
- \(\ \lim _{x \rightarrow \infty}-5 x^{2}+5 x+14\)
- \(\ \lim _{x \rightarrow \infty} 7 x+12\)
- \(\ \lim _{x \rightarrow \infty}-3 x+13\)
- \(\ \lim _{x \rightarrow \infty} \frac{13 x-8}{19 x^{3}-11 x^{2}+x+4}\)
- \(\ \lim _{x \rightarrow \infty}-17 x+14\)
- \(\ \lim _{x \rightarrow \infty}-7 x^{2}-2 x-13\)
Vocabulary
| Term | Definition |
|---|---|
| limit | A limit is the value that the output of a function approaches as the input of the function approaches a given value. |