6.3.3: Hyperbolas with any Center
- Page ID
- 14760
Hyperbolas Centered at (h, k)
Your homework assignment is to graph the hyperbola \(\ 9(y+2)^{2}-4(x-3)^{2}=36\). What are the vertices of your graph?
Hyperbolas Centered at (h,k)
Just like you have learned previously, a hyperbola does not always have to be placed with its center at the origin. If the center is \(\ (h,k)\) the entire ellipse will be shifted \(\ h\) units to the left or right and \(\ k\) units up or down. The equation becomes \(\ \frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1\). We will address how the vertices, co-vertices, and foci change in the next problem.
Let's graph \(\ \frac{(x-2)^{2}}{16}-\frac{(y+1)^{2}}{9}=1\). Then, let's find the vertices, foci, and asymptotes.
First, we know this is a horizontal hyperbola because the \(\ x\) term is first. Therefore, the center is \(\ (2,−1)\) and \(\ a=4\) and \(\ b=3\). Use this information to graph the hyperbola.
To graph, plot the center and then go out 4 units to the right and left and then up and down 3 units. Draw the box and asymptotes.
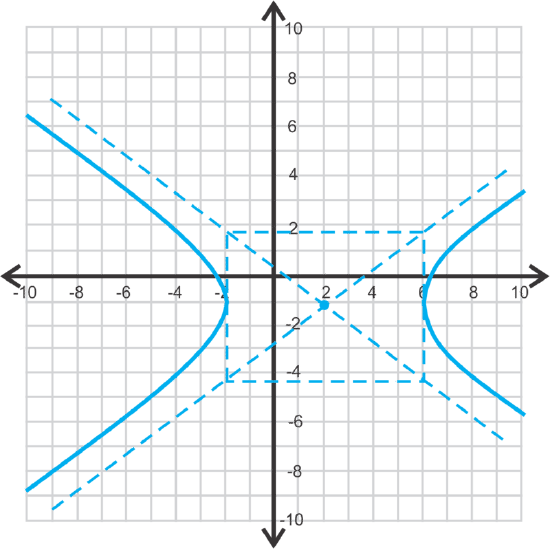
This is also how you can find the vertices. The vertices are \(\ (2 \pm 4,-1)\) or \(\ (6,-1)\) and \(\ (-2,-1)\).
To find the foci, we need to find \(\ c\) using \(\ c^{2}=a^{2}+b^{2}\).
\(\ \begin{array}{l}
c^{2}&=16+9=25 \\
c&=5
\end{array}\)
Therefore, the foci are \(\ (2 \pm 5,-1)\) or \(\ (7,−1)\) and \(\ (−3,−1)\).
To find the asymptotes, we have to do a little work to find the y-intercepts. We know that the slope is \(\ \pm \frac{b}{a}\) or \(\ \pm \frac{3}{4}\) and they pass through the center. Let’s write each asymptote in point-slope form using the center and each slope.
\(\ y-1=\frac{3}{4}(x+2)\) and \(\ y-1=-\frac{3}{4}(x+2)\)
Simplifying each equation, the asymptotes are \(\ y=\frac{3}{4} x-\frac{5}{2}\) and \(\ y=-\frac{3}{4} x+\frac{1}{2}\).
From this problem, we can create formulas for finding the vertices, foci, and asymptotes of a hyperbola with center \(\ (h,k)\). Also, when graphing a hyperbola, not centered at the origin, make sure to plot the center.
| Orientation | Equation | Vertices | Foci | Asymptotes |
|---|---|---|---|---|
| Horizontal | \(\ \frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1\) | \(\ (h \pm a, k)\) | \(\ (h \pm c, k)\) | \(\ y-k=\pm \frac{b}{a}(x-h)\) |
| Vertical | \(\ \frac{(y-k)^{2}}{a^{2}}+\frac{(x-h)^{2}}{b^{2}}=1\) | \(\ (h, k \pm a)\) | \(\ (h, k \pm c)\) | \(\ y-k=\pm \frac{a}{b}(x-h)\) |
Now, let's find the equation of the hyperbola with vertices \(\ (−3,2)\) and \(\ (7,2)\) and focus \(\ (−5,2)\).
These two vertices create a horizontal transverse axis, making the hyperbola horizontal. If you are unsure, plot the given information on a set of axes. To find the center, use the midpoint formula with the vertices.
\(\ \left(\frac{-3+7}{2}, \frac{2+2}{2}\right)=\left(\frac{4}{2}, \frac{4}{2}\right)=(2,2)\)
The distance from one of the vertices to the center is \(\ a,|7-2|=5\). The distance from the center to the given focus is \(\ c,|-5-2|=7\). Use \(\ a\) and \(\ c\) to solve for \(\ b\).
\(\ \begin{array}{l}
7^{2}=5^{2}+b^{2} \\
b^{2}=24 \rightarrow b=2 \sqrt{6}
\end{array}\)
Therefore, the equation is \(\ \frac{(x-2)^{2}}{25}-\frac{(y-2)^{2}}{24}=1\).
Finally, let's graph \(\ 49(y-3)^{2}-25(x+4)^{2}=1225\) and find the foci.
First we have to get the equation into standard form, like the equations above. To make the right side 1, we need to divide everything by 1225.
\(\ \begin{array}{c}
\frac{49(y-3)^{2}}{1225}-\frac{25(x+4)^{2}}{1225}=\frac{1225}{1225} \\
\frac{(y-3)^{2}}{25}-\frac{(x+4)^{2}}{49}=1
\end{array}\)
Now, we know that the hyperbola will be vertical because the y-term is first.
\(\ a=5\), \(\ b=7\) and the center is \(\ (−4,3)\).
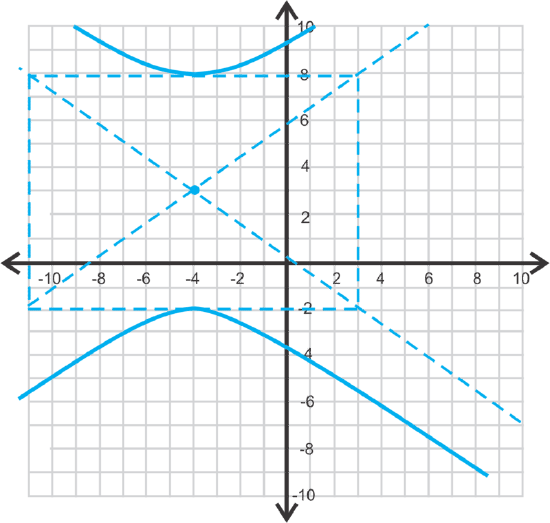
To find the foci, we first need to find \(\ c\) by using \(\ c^{2}=a^{2}+b^{2}\).
\(\ \begin{aligned}
c^{2} &=49+25=74 \\
c &=\sqrt{74}
\end{aligned}\)
The foci are \(\ (-4,3 \pm \sqrt{74})\) or \(\ (−4,11.6)\) and \(\ (−4,−5.6)\).
Examples
Earlier, you were asked to identify the vertices of the graph of the hyperbola defined by \(\ 9(y+2)^{2}-4(x-3)^{2}=36\).
Solution
First we need to get the equation in standard form \(\ \frac{(y-k)^{2}}{a^{2}}+\frac{(x-h)^{2}}{b^{2}}=1\), so we divide by \(\ 36\).
\(\ \begin{array}{r}
9(y+2)^{2}-4(x-3)^{2}=&36 \\
\frac{9(y+2)^{2}}{36}-\frac{4(x-3)^{2}}{36}=&\frac{36}{36} \\
\frac{(y+2)^{2}}{4}-\frac{(x-3)^{2}}{9}=&1
\end{array}\)
Because the y-term is first, we can now see that the vertices are \(\ (h, k \pm a)(3,-2 \pm 2)\). That is, \(\ (3,0)\) and \(\ (3,−4)\)
Find the center, vertices, foci, and asymptotes of \(\ \frac{(y-1)^{2}}{81}-\frac{(x+5)^{2}}{16}=1\).
Solution
The center is \(\ (−5,1)\), \(\ a=\sqrt{81}=9\) and \(\ b=\sqrt{16}=4\), and the hyperbola is horizontal because the y-term is first. The vertices are \(\ (-5,1 \pm 9)\) or \(\ (-5,10)\) and \(\ (−5,−8)\). Use \(\ c^{2}=a^{2}+b^{2}\) to find \(\ c\).
\(\ \begin{aligned}
c^{2} &=81+16=97 \\
c &=\sqrt{97}
\end{aligned}\)
The foci are \(\ (-5,1+\sqrt{97})\) and \(\ (-5,1-\sqrt{97})\).
The asymptotes are \(\ y-1=\pm \frac{9}{4}(x+5)\) or \(\ y=\frac{9}{4} x+12 \frac{1}{4}\) and \(\ y=-\frac{9}{4} x-10 \frac{1}{4}\).
Graph \(\ 25(x-3)^{2}-4(y-1)^{2}=100\) and find the foci.
Solution
Change this equation to standard form in order to graph.
\(\ \begin{array}{l}
\frac{25(x-3)^{2}}{100}-\frac{4(y-1)^{2}}{100}&=\frac{100}{100} \\
\frac{(x-3)^{2}}{4}-\frac{(y-1)^{2}}{25}&=1
\end{array}\)
center: \(\ (3,1), a=2, b=5\)
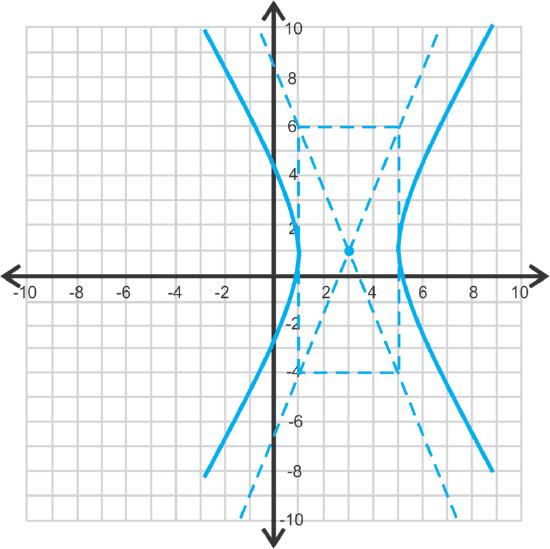
Find the foci.
\(\ \begin{array}{l}
c^{2}&=25+4=29 \\
c&=\sqrt{29}
\end{array}\)
The foci are \(\ (3,1+\sqrt{29})\) and \(\ (3,1-\sqrt{29})\).
Find the equation of the hyperbola with vertices \(\ (−6,−3)\) and \(\ (−6,5)\) and focus \(\ (−6,7)\).
Solution
The vertices are \(\ (−6,−3)\) and \(\ (−6,5)\) and the focus is \(\ (−6,7)\). The transverse axis is going to be vertical because the x-value does not change between these three points. The distance between the vertices is \(\ |-3-5|=8\) units, making \(\ a=4\). The midpoint between the vertices is the center.
\(\ \left(-6, \frac{-3+5}{2}\right)=\left(-6, \frac{2}{2}\right)=(-6,1)\)
The focus is \(\ (−6,7)\) and the distance between it and the center is 6 units, or \(\ c\). Find \(\ b\).
\(\ \begin{aligned}
36 &=b^{2}+16 \\
20 &=b^{2} \\
b &=\sqrt{20}=2 \sqrt{5}
\end{aligned}\)
The equation of the hyperbola is \(\ \frac{(y-1)^{2}}{16}-\frac{(x+6)^{2}}{20}=1\).
Review
Find the center, vertices, foci, and asymptotes of each hyperbola below.
- \(\ \frac{(x+5)^{2}}{25}-\frac{(y+1)^{2}}{36}=1\)
- \(\ (y+2)^{2}-16(x-6)^{2}=16\)
- \(\ \frac{(y-2)^{2}}{9}-\frac{(x-3)^{2}}{49}=1\)
- \(\ 25 x^{2}-64(y-6)^{2}=1600\)
- \(\ (x-8)^{2}-\frac{(y-4)^{2}}{9}=1\)
- \(\ 81(y+4)^{2}-4(x+5)^{2}=324\)
- Graph the hyperbola in #1.
- Graph the hyperbola in #2.
- Graph the hyperbola in #5.
- Graph the hyperbola in #6.
Using the information below, find the equation of each hyperbola.
- vertices: \(\ (−2,−3)\) and \(\ (8,−3)b=7\)
- vertices: \(\ (5,6)\) and \(\ (5,−12)\) focus: \(\ (5,−15)\)
- asymptote: \(\ y+3=\frac{4}{9}(x+1)\) horizontal transverse axis
- foci: \(\ (−11,−4)\) and \(\ (1,−4)\) vertex: \(\ (−8,−4)\)
- Extension Rewrite the equation of the hyperbola,
- \(\ x^{2}-4 y^{2}+490 x-16 y+1013=0\) in standard form, by completing the square for both the \(\ x\) and \(\ y\) terms.
Answers for Review Problems
To see the Review answers, open this PDF file and look for section 10.9.
Image Attributions
- [Figure 1]
Credit: Ben Salter
Source: https://www.flickr.com/photos/ben_salter/2348052408

