2.3: Limits of Polynomial and Rational Functions

Polynomial Functions

Recall that a function f(x) polynomial function if it satisfies:

\[f(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{2} x^{2}+a_{1} x+a_{0}\]

for all x, where n is a non-negative integer and \(a_0\), \(a_1\), \(a_2\), …, \(a_n\) are constant coefficients.

As a refresher, use the limit properties to find limit of (x²−3x+4) as x→20, i.e., the limit as x approaches a particular value.

The function is a polynomial, a quadratic trinomial that is graphed below, and can be treated as the sum of three functions. This means that we can use the rule “the limit of the sum is the sum of the limits” in the determination of the limit.

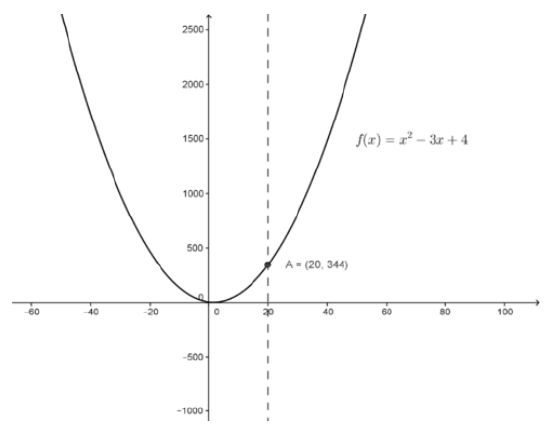
CC BY-NC-SA

Since, the polynomial can be treated as the sum of three functions, we can use the property “the limit of the sum is the sum of the limits” in the determination of the limit.

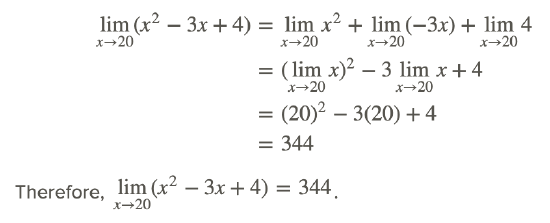
Note that the value of this limit could have been found by direct substitution of x=1 in the polynomial function.

Now, find

\[\lim _{x \rightarrow \infty}\left(x^{2}-3 x+4\right)\]

i.e., the limit as x approaches infinity. This is looking at end behavior.

The polynomial can be treated as the product of two functions. This means that we can use the rule “the limit of the product of functions is the product of the limits of each function” in the determination of the limit.

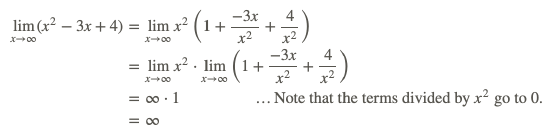
Therefore,

\[\lim _{x \rightarrow \infty}\left(x^{2}-3 x+4\right)=\infty.\]

A similar evaluation shows that

\[\lim _{x \rightarrow-\infty}\left(x^{2}-3 x+4\right)=\infty.\]

This behavior depicts the fact that the end behavior of polynomials goes as the term with the highest degree, and values grow without bound.

The results of these two examples can be generalized to the following properties:

Given the polynomial function f(x)=p(x):

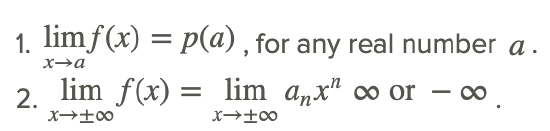
Rational Functions

Now let’s consider limits of rational functions. A rational function is the ratio of two polynomials. In the case of a single variable, x, a function is called a rational function if and only if it can be written in the form:

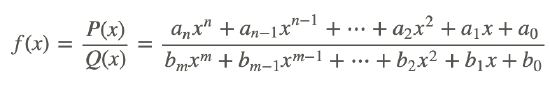
where P(x) and Q(x) are polynomial functions in x and Q(x) is non-zero. The domain of f is the set of all values of x for which the denominator Q(x) is not zero.

The function is shown in the graph below.

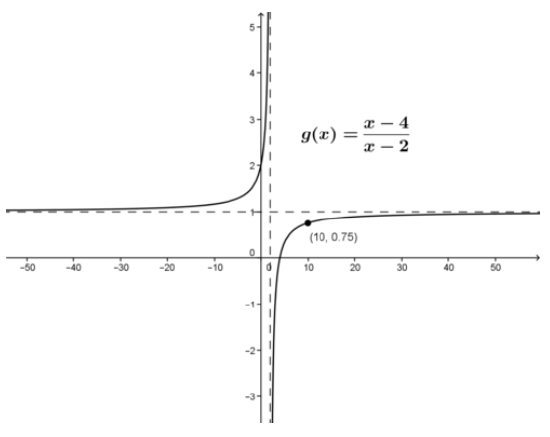
CC BY-NC-SA

We note first that the denominator of the rational function is not zero at the value x=10. The quotient rule can therefore be used to start the evaluation of the function as follows:

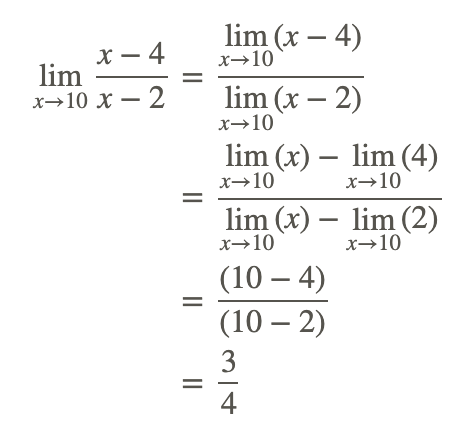
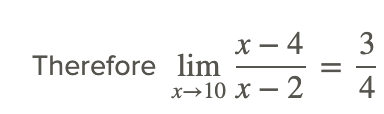
Note that because the denominator does not equal 0 at x=10, the limit could have been found by direct substitution of x=10 in the rational function.

Now, find the end behavior of that same function, i.e. find

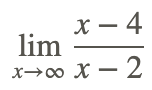
The following steps are used to evaluate the limit at as x approaches infinity.

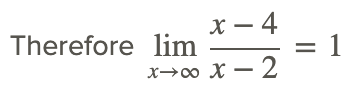
The above problems illustrate the evaluation of the limit of a rational function at a value of x for which the denominator does not equal 0. Sometimes finding the limit of a rational function f(x) at some x=a can entail more work than just direct substitution because the denominator equals zero at x=a. What if the denominator is equal to 0?

Notice that the function here is indeterminate at x=2, so that direct substitution does not work. However, in this case it is possible to remove the zero in the denominator by factoring the numerator and canceling the factor (x−2) from both the numerator and the denominator.

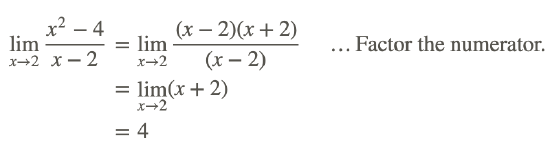
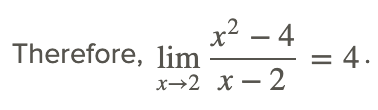
The factoring of the numerator shown above, and then cancelling any common factors in the denominator, is a common technique used to find the limits of rational functions at points where the denominator is 0. Always check to see if the function can be simplified to remove the zero in the denominator, especially by cancelling common a factor that removes a discontinuity.

Now, find

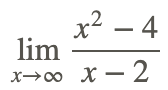
We look at the end behavior of the function as x goes to infinity as follows:

Therefore,

\[\lim _{x \rightarrow \infty} \frac{x^{2}-4}{x-2}=\infty\]

The end behavior as x goes to −∞ can be determined by a similar approach, and is found to be −∞.

Definition of the Limit of Rational Functions

For the rational function f(x)=^p(x)/_q(x) and any real number a,

\[\lim _{x \rightarrow a} f(x)=\frac{p(a)}{q(a)}\) if \(q(a) \neq 0\]

If q(a)=0, then the function may or may not have a limit.

For the rational function

---

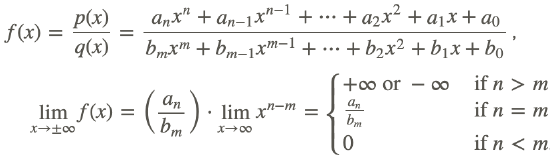
Examples

Example 1

Earlier, you were asked about the respective difficulties of finding the limit of polynomial and rational functions. Finding the limit of a polynomial function is relatively easy because a polynomial function can be evaluated at any value of the independent variable so that the limit at a specific value can be evaluated by direct substitution. The limit as the independent variable goes to ±∞ is just ±∞ depending whether the degree of the polynomial is even or odd.

Evaluating the limit of a rational function can be more difficult because direct substitution may lead to an undefined or indeterminate form that requires a different approach, and the limit as the independent variable goes to ±∞ depends on which is larger, the degree of the numerator polynomial or the degree of denominator polynomial.

Example 2

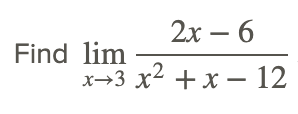
The numerator and the denominator are both equal to zero at x=3, but there is a common factor x−3 that can be removed (that is, we can simplify the rational function):

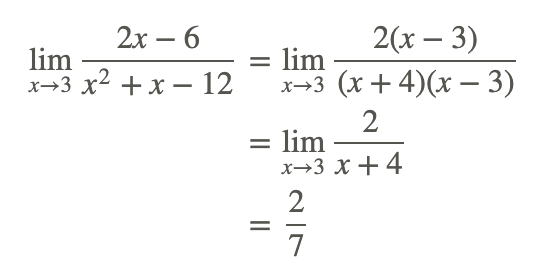
Example 3

Find

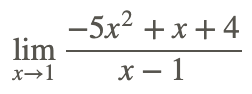
to find

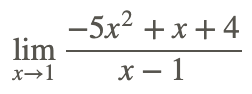
..... Start by factoring the numerator

Since we have (x−1) in both numerator and denominator, we know that the original function is equal to just −5x−4 except where it is undefined (1).

Therefore the closer we get to inputing 1, the closer we get to the same value, whether from the + or - side.

To find the value, just solve

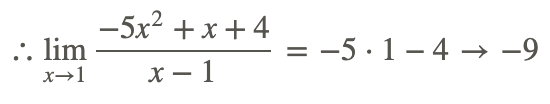
Example 4

Find

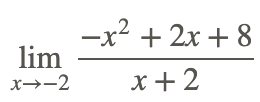
to find

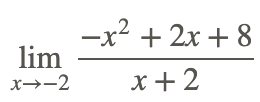
.... Start by factoring the numerator

Since we have (x+2) in both numerator and denominator, we know that the original function is equal to just −x−4

Therefore the closer we get to substituting -2, the closer we get to the same output value, whether from the + or - side.

To find the value, just solve −x−4 for x=−2

---

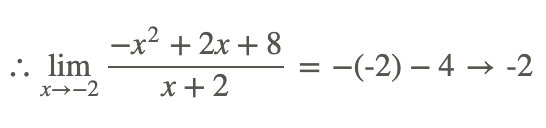
Review

Solve the following rational function limits.

---

Review (Answers)

To see the Review answers, open this PDF file and look for section 2.5.

---

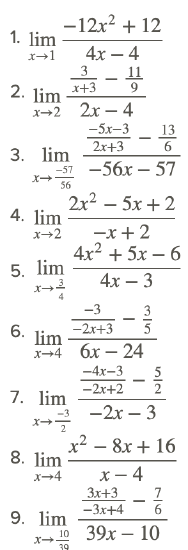
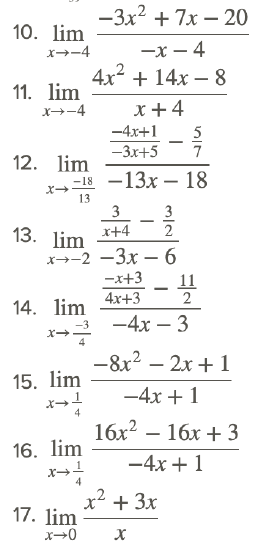
Vocabulary

Term	Definition
discontinuous	A function is discontinuous if the function exhibits breaks or holes when graphed.
limit	A limit is the value that the output of a function approaches as the input of the function approaches a given value.
Polynomial Function	A polynomial function is a function defined by an expression with at least one algebraic term.
Rational Function	A rational function is any function that can be written as the ratio of two polynomial functions.

---

Additional Resources

PLIX: Play, Learn, Interact, eXplore - Evaluating Limits of Rational Functions

Video: Limit Examples

Practice: Limits of Polynomial and Rational Functions

Real World: Webslingers