2.5: Limits Involving Radical Functions
- Page ID
- 1116
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)There are many problems that will involve taking the nth root of a variable expression, so it is natural that there may sometimes be a need to find the limit of a function involving radical expressions, using square or cube roots, or other roots. Do you think that finding the limit of a function involving radicals would be any different than finding the limit of polynomial or rational functions? Can you think of any ways that radicals might present different problems than polynomials?
Limits with Radical Functions
When evaluating a limit involving a radical function, use direct substitution to see if a limit can be evaluated whenever possible. If not, other methods to evaluate the limit need to be explored.
Take the following function

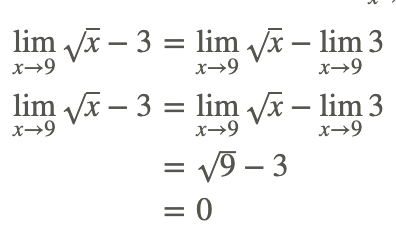
Therefore,
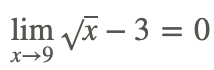
which could have been determined by directly evaluating f(x) at x=9, i.e., by using direct substitution.
Now, find
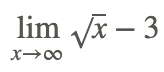
In both of the above cases, direct substitution could be used to evaluate the limits and there is no need for alternative methods.
Take a look at the function

First we notice that we should exclude x=−5/7 in any evaluation. Using direct substitution to find the limit results in the indeterminate form ∞/∞. To transform the radical expression to a better form, use the fact that the value of x is going to larger and larger positive values. This allows the following:
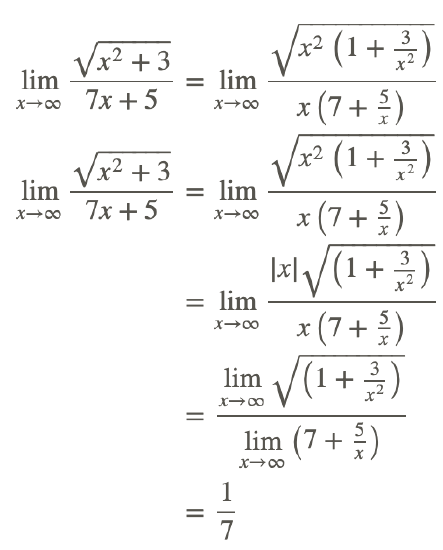
Therefore,
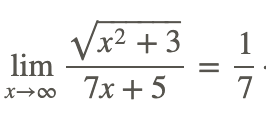
Now, find
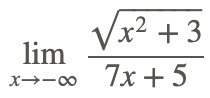
The solution to evaluating the limit at negative infinity is similar to the above approach except that x is always negative.

Therefore.
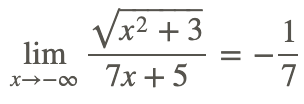
So far, you have been able to find the limit of rational functions using methods shown earlier. However, there are times when this is not possible. Take the function
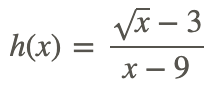
Find
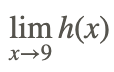
Using direct substitution to find the limit results in the indeterminate form 00. In order to evaluate the limit, we need to transform the expression to remove the indeterminate form. This is accomplished by using the relationship for the difference of squares of real numbers: x2−y2=(x+y)(x−y).
We then rewrite and simplify the original function as follows:
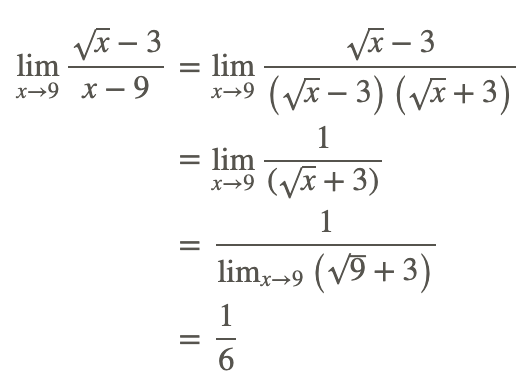
Use the difference of squares factoring to remove the 0 in the denominator.
Hence
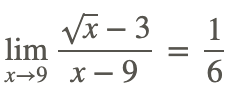
Now, find the end behavior of the same function, i.e. find
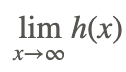
As x increases to large positive values, the function takes on the indeterminate form ∞/∞. The transformation above can also be used to evaluate the limit (Approach 1), as well as the technique used in evaluating rational functions (Approach 2).

Hence
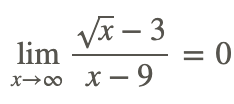
Finally, find
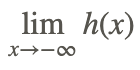
The solution to this problem is that the limit does not exist because the domain of h(x) does not include x<0.
Examples
Example 1
Earlier, you were asked if the methods for evaluating limits involving polynomials and rational functions can be used to find the limits of radical functions. Some of the methods do work for radical functions. The use of direct substitution is a common method. Transforming indeterminate or undefined forms by finding and canceling common factors in the numerator and denominator, or factoring and simplifying the highest degree powers of variables represent common approaches.
One of the noteworthy differences between polynomial and radical functions is that the domain of polynomials can include all real values of the independent variable, but the domain of radical functions, e.g., x√, is restricted.
Example 2
Find
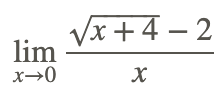
Using direct substitution to find the limit of the function results in the indeterminate form 0/0. To transform the radical expression to a better form, do the following:
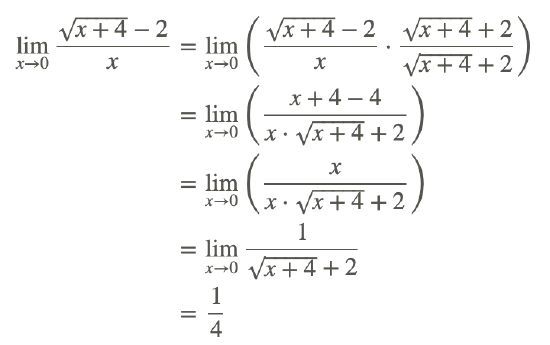
…Rationalize the numerator: multiply by the conjugate of the numerator
Therefore,
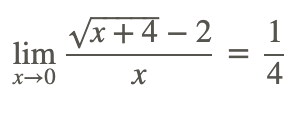
Review
Find each of the following limits if they exist.
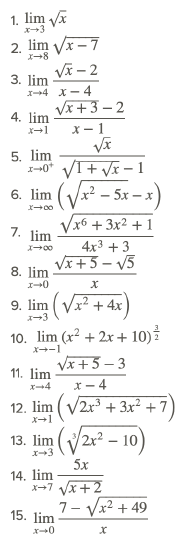
Vocabulary
| Term | Definition |
|---|---|
| indeterminate | In mathematics, an expression is indeterminate if it is not precisely defined. There are seven indeterminate forms: 0/0,0⋅∞,∞/∞,∞−∞,00,∞0, and 1^\infty. |
| limit | A limit is the value that the output of a function approaches as the input of the function approaches a given value. |
| radical function | Radical functions are functions which contain nth roots of variable expressions. |
Additional Resources
Video: Limits at Infinity
Practice: Limits Involving Radical Functions
Real World: Maverick Surfers

