6.2: Related Rates
- Page ID
- 1208
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In the concept on implicit differentiation, you learned that given a relationship between two quantities, the relationship between their respective rates of change can be determined. This is often an invaluable tool in applications, since it allows us to find the rate at which some quantity is changing by relating it to other quantities whose rates of change are known (or at least more easily found). For example, if you were at the scene of an accident where an oil spill from a large tanker is spreading in a circular pattern whose radius you determine is increasing by about 1 ft per second, would you be able to tell someone how fast the oil spill area was increasing when the radius was about 30 feet?
Related Rates
What do we mean by related rates? These are simply the derivatives, rates, of one or more parameters that are related to each other through an equation. The relationship between the rates is obtained by taking the derivative of some other relationship between the parameters.
A simple example with a familiar geometric shape should help illustrate the concept.
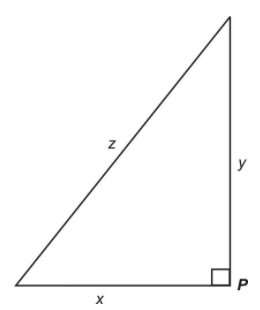
Consider the simple right triangle in the figure below with sides x,y, and z. The relationship between the sides is governed by the Pythagorean Theorem.
\[ x^2+y^2=z^2 \nonumber\]
CC BY-NC-SA
We could easily attach some real-life situation to this geometric figure. Say for instance that x and y represent the paths of two people starting at point p and walking North and West, respectively, for two hours. The quantity z represents the distance between them at any time t. Let’s now determine any relationships between the various rates of change that we get by implicitly differentiating the original equation x2+y2=z2 with respect to time t.
\[ \frac{d}{dt}[x^2+y^2]=\frac{d}{dt}[z^2] \nonumber\]
\[ 2x\frac{dx}{dt}+2y\frac{dy}{dt}=2z\frac{dz}{dt} \nonumber\]
\[ x\frac{dx}{dt}+y\frac{dy}{dt}=z\frac{dz}{dt} \nonumber\]
…Equation 1
Implicit differentiation of the Pythagorean relationship between the side lengths has yielded relationships between the side length derivatives, and since the derivatives are rates, this is an example of related rates.
How might the relationship above be used to solve or answer a problem?
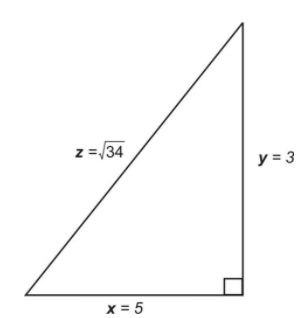
Let’s say that person is walking in the x-direction at 5 mph, and that another person is walking in the y-direction at 3 mph. The distance, z, between the walkers is changing with time, and the time rate of change of, z, dz/dt, is dependent on the rates at which the two people are walking.
One problem that we could pose is:
At what rate is the distance between x and y increasing after one hour? That is, what is dzdt after one hour?
Assume that they have walked for one hour. So x=5 mi and y=3.
Using the Pythagorean Theorem, we find the distance between them after one hour is \[ z=\sqrt{34}=5.83 \nonumber\]
CC BY-NC-SA
If we substitute the values for x,y, and z into Equation 1 along with the individual rates we get
\[ 5(5)+3(3)=\sqrt{34}\frac{dz}{dt} \nonumber\]
\[ 34=\sqrt{34}\frac{dz}{dt} \nonumber\]
\[ \frac{34}{\sqrt{34}}=\frac{dz}{dt} \nonumber\]
Hence after one hour the distance between the two people is increasing at a rate of:
\[ \frac{dz}{dt}=\frac{34}{\sqrt{34}}≈5.83 mph \nonumber\]
Suppose we have a rectangular field and we know that at an instant of time, the length is changing at the rate of 8 ft/hour and the perimeter is changing at a rate of 24 ft/hour. At what rate is the width changing at that instant? At what rate is the area changing at that instant?
You are familiar with the formulas for Perimeter:
\[ P=2l+2w \nonumber\]
If we differentiate the perimeter equation, we have
Equation 2: \[ \frac{dP}{dt}=2\frac{dl}{dt}+2\frac{dw}{dt} \nonumber\]
Substituting our known information into Equation 2, we have
\[ 24=(2×8)+2×\frac{dw}{dt} \nonumber\]
\[ 8=2×\frac{dw}{dt} \nonumber\]
\[ 4=\frac{dw}{dt} \nonumber\]
The width is changing at a rate of 4 ft/hr.
Examples
Example 1
Earlier, you were asked about being at the scene of an accident where an oil spill from a large tanker is spreading in a circular pattern whose radius you determine is increasing by about 1 ft per second. Would you be able to tell someone how fast the oil spill area was increasing when the radius was about 30 feet?
Since the circular area of the spill is \[ A=πr^2 \nonumber\] the time rate of change of the area is \[ \frac{dA}{dt}=π2r\frac{dr}{dt} \nonumber\] This means that with \[ \frac{dr}{dt}=1 \frac{ft}{s} \nonumber\] when r=30 ft, \[ \frac{dA}{dt}=60π \frac{ft^2}{s} \nonumber\]
Example 2
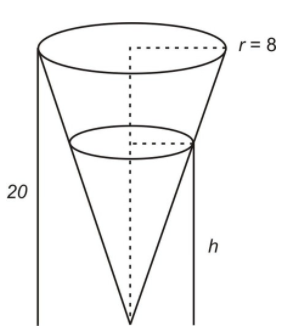
We have a water tank shaped as an inverted right circular cone. Suppose that water flows into the tank at the rate of 5 ft3/min. At what rate is the water level rising when the height of the water in the tank is 6 feet?
CC BY-NC-SA
We know that the volume of water in the water tank is:
\[ V=\frac{1}{3} \pi r^2h \nonumber\]
When we differentiate this equation we get:
\[ \frac{dV}{dt}=\frac{1}{3} \pi (h)(2r)\frac{dr}{dt}+\frac{1}{3} \pi r^2\frac{dh}{dt} \nonumber\]
This is a related rates equation. The rate dV/dt is related to the rates dr/dt and dh/dt.
We know \[ \frac{dV}{dt}=5 \frac{ft^3}{min} \nonumber\] do no know dr/dt, but want to find dh/dt. We need to somehow find a relationship between h and r.
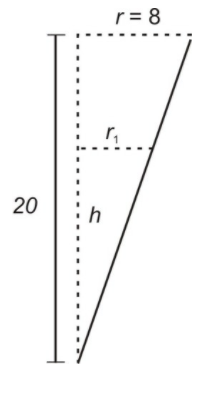
Let r1 be the radius of the surface of the water as it flows out of the tank.
CC BY-NC-SA
Note that the two triangles are similar and thus corresponding parts are proportional. In particular,
\[ \frac {r_1}{h} = \frac{8}{20} \nonumber\]
\[ r_1 = \frac{8h}{20} = \frac{2h}{5} \nonumber\]
We can write this as a general relationship between r and h.
\[ r = \frac{2h}{5} \nonumber\]
which means also that
\[ \frac{dr}{dt} =\frac{2}{5} \frac{dh}{dt} \nonumber\]
We have the relationships we need.
Now we can solve the problem in a couple of ways: (a) substitute
\[ r = \frac{2h}{5} \nonumber\] into the original equation for V, or (b) substitute
\[ r = \frac{2h}{5} \nonumber\] and
\[ \frac{dr}{dt} =\frac{2}{5} \frac{dh}{dt} \nonumber\] into the equation for \[ \frac{dV}{dt} \nonumber\]
Let’s try approach (a).
\[ V = \frac{1}{3} \pi (\frac{2h}{5})^2 h = \frac{4 \pi}{75} h^3 \nonumber\]
Hence
\[ \frac{dV}{dt} = \frac{12 \pi}{75} h^2 \frac{dh}{dt} \nonumber\]
and by substitution,
\[ 5 = \frac{12 \pi}{75} (36) \frac{dh}{dt} \nonumber\]
\[ \frac{dh}{dt} = \frac{375}{432 \pi} \approx 0.28 \frac{ft}{min} \nonumber\]
Review
- Make up a related rates problem about the area of a rectangle. Illustrate the solution to your problem.
- Suppose that a particle is moving along the curve 4x2+16y2=32. When it reaches the point (2, 1), the x-coordinate is increasing at a rate of 3 ft/sec. At what rate is the y-coordinate changing at that instant?
- A regulation softball diamond is a square with each side of length 60 ft. Suppose a player is running from first base to second base at a speed of 18 ft/sec. At what rate is the distance between the runner and home plate changing when the runner is 2/3 of the way from first to second base?
- At a recent Hot Air Balloon festival, a hot air balloon was released. Upon reaching a height of 300 ft, it was rising at a rate of 20 ft/sec. Mr. Smith was 100 ft away from the launch site watching the balloon. At what rate was the distance between Mr. Smith and the balloon changing at that instant?
- Two trains left the St. Louis train station in the late morning. The first train was traveling East at a constant speed of 65 mph. The second train traveled South at a constant speed of 75 mph. At 3 PM, the first train had traveled a distance of 120 miles while the second train had traveled a distance of 130 miles. How fast was the distance between the two trains changing at that time?
- Suppose that a 17 ft ladder is sliding down a wall at a rate of -6 ft/sec. At what rate is the bottom of the ladder moving when the top is 8 ft from the ground?
- Suppose that the length of a rectangle is increasing at the rate of 6 ft/min and the width is increasing at a rate of 2 ft/min. At what rate is the area of the rectangle changing when its length is 25 ft and its width is 15 ft?
- Suppose that the quantity demand of new 40′′ plasma TVs is related to its unit price by the formula p+x2=1200, where p is measured in dollars and x is measured in units of one thousand. How is the quantity demand changing when x=20,p=1500, and the price per TV is decreasing at a rate of $10?
- The volume of a cube with side s is changing. At a certain instant, the sides of the cube are 6 inches and increasing at the rate of 1/4 in/min. How fast is the volume of the cube increasing at that time?
- (1) Suppose that the area of a circle is increasing at a rate of 24 in2/min. How fast is the radius increasing when the area is 36π in2? (2) How fast is the circumference changing at that instant?
- The radius of a circle is getting bigger at a rate of 5 centimeters per second. How fast is the area of the circle increasing when the radius is equal to ten centimeters?
- The area of a circle is expanding at a rate of 100 square centimeters a second at an instant when its radius is expanding at a rate of 50 centimeters a second. What is the circle’s radius at that instant?
- At a given instant, the volume of a cylinder with a cross sectional area of 6 square centimeters is increasing at a rate of 10 cubic centimeters a second. What is the rate of increase of its height at that instant?
- Express the rate of change of a cylinder’s volume as a function of its radius, its height, and the rate of change of its radius, if its height is assumed to be held constant.
- A four dimensional object whose momentum is given by the formula \[ M=sin( \pi x_1)+δx_2^3+ln(x_3x_4)x_1^5, where delta is a constant, is falling into a black hole. The resulting compression causes its x1 value to shrink at a rate of 8 million miles a second (while the other variables remain constant.) If \[ x_3= \frac{5}{x_4} \nonumber\] what is the instantaneous change in its momentum when x1=1?
Vocabulary
| Term | Definition |
|---|---|
| derivative | The derivative of a function is the slope of the line tangent to the function at a given point on the graph. Notations for derivative include f′(x), dydx, y′, dfdx and \frac{df(x)}{dx}. |
| related rates | Related rates are derivatives of variables that are common (related) to one or more linked equations. |
Additional Resource
Video - Ladder Rate-Of-Change Problem
Practice - Related Rates
Real World - Chain Reaction

