7.5: Concavity and Inflection
- Page ID
- 1217
When defined at a point, the first derivative and the second derivative each provide one of three results: + (value > 0), - (value < 0) or 0. What are all of the result possibilities for f′ and f′′, and which give definitive information on the extrema of f?
Applying the Derivative Tests
Now we will apply all that we have learned from the First and Second Derivative Tests to sketch graphs of functions. The following table provides a summary of the tests and can be a useful guide in sketching graphs.
|
Signs of 1st and 2nd derivatives |
Conclusion |
Shape of the graphs |
|
f′(x)>0 + f′′(x)>0 + |
f is increasing f is concave upward |
CC BY-NC-SA |
|
f′(x)>0 + f′′(x)<0 − |
f is increasing f is concave downward |
CC BY-NC-SA |
|
f′(x)<0 − f′′(x)>0 + |
f is decreasing f is concave upward |
CC BY-NC-SA |
|
f′(x)<0 − f′′(x)<0 − |
f is decreasing f is concave downward |
CC BY-NC-SA |
Take a look at an example where we can use both the First and Second Derivative Tests to find out information that will enable us to sketch the graph.
Let’s examine the function \( f(x)=x^5−5x+2 \nonumber\).
- Find the critical values for which f′(c)=0.
\( f′(x)=5x^4−5=0 \nonumber\), which means \( x^4−1=0 \nonumber\) at x=±1.
- Apply the First and Second Derivative Tests to determine extrema and points of inflection.
We note the signs of f′ and f′′ in the intervals partitioned by x=±1,0.
|
Key intervals |
f′(x) | f′′(x) |
Shape of graph |
| x<−1 | + | − |
Increasing, concave down |
| −1<x<0 | − | − |
Decreasing, concave down |
| 0<x<1 | − | + |
Decreasing, concave up |
| x>1 | + | + |
Increasing, concave up |
At the critical points:
- f′′(−1)=−20<0. By the Second Derivative Test we have a relative maximum at x=−1, or the point (-1, 6).
- f′′(0)=0. By the Second Derivative Test we must have a point of inflection due to the transition from concave down to concave up between the key intervals.
- f′′(1)=20>0. By the Second Derivative Test we have a relative minimum at x=1, or the point (1, -2).
Now we can sketch the graph.
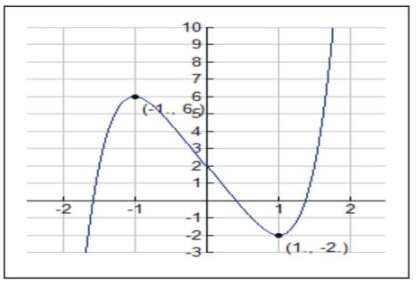
CC BY-NC-SA
Now, look at a simple rational function.
Consider the function f(x)=x+2x−3.
- Find the critical values for which f′(c)=0.
\( f′(x)= \frac{1}{x−3}+(x+2) \frac{−1}{(x−3)^2}= \frac{−5}{(x−3)^2} \nonumber\) which means there are no values c that make f′(c)=0.
Since f′(x) is not defined at x=3, this is the one critical point.
- We note the signs of f′ and f′′ in the intervals partitioned by x=3.
|
Key intervals |
f′(x) | f′′(x) |
Shape of graph |
| x<3 | − | − |
Decreasing, concave down |
| x>3 | − | + |
Decreasing, concave up |
At the critical point, there is a vertical asymptote and the function and derivatives are undefined; there are no minima or maxima.
Now we can sketch the graph.
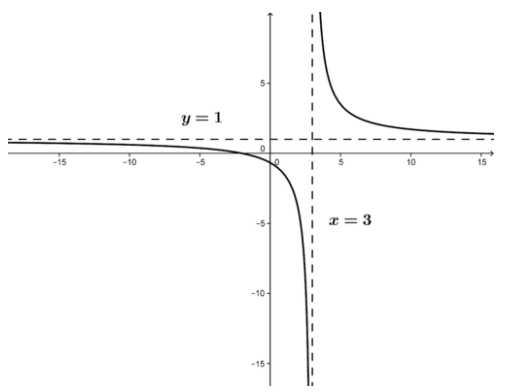
CC BY-NC-SA
Examples
Example 1
Earlier, you were asked to chart all of the sign/zero possibilities for f′ and f′′, and identify which give definitive information on the extrema of f.
There are nine possibilities as follows:
| f′ | f′′ |
Definitive Extrema Info? |
| + | + |
No |
| + | − |
No |
| + | 0 |
No |
| − | + |
No |
| − | − |
No |
| − | 0 |
No |
| 0 | + |
Yes |
| 0 | − |
Yes |
| 0 | 0 |
No |
Only when there is a critical point with f′=0 can we use the information on f′′ to tell whether we have a minimum or a maximum of f.
Example 2
For the function \( f(x)= \frac{x^2−4x+4}{x^2+1} \nonumber\), find all critical values, the corresponding y values for each critical value, and classify each point as a relative maximum or a relative minimum
The derivative is: \( f′(x)= \frac{2(2x^2−3x−2)}{(x^2+1)^2} \nonumber\)
Which gives critical values: x=−12 and x=2
This means that: \( f(−\frac{1}{2})=5 \nonumber\) and \( f(2)=0 \nonumber\)
The second derivative is: \( f′′(x)=− \frac{2(4x^3+9x^2+4x+5)}{(x^2+1)^3} \nonumber\)
Evaluation at the critical points determines that \( f′′(−\frac{1}{2})<0 \nonumber\), which means concave down (a maximum), and f′′(2)>0 means concave up (a minimum).
The function graph is plotted below:
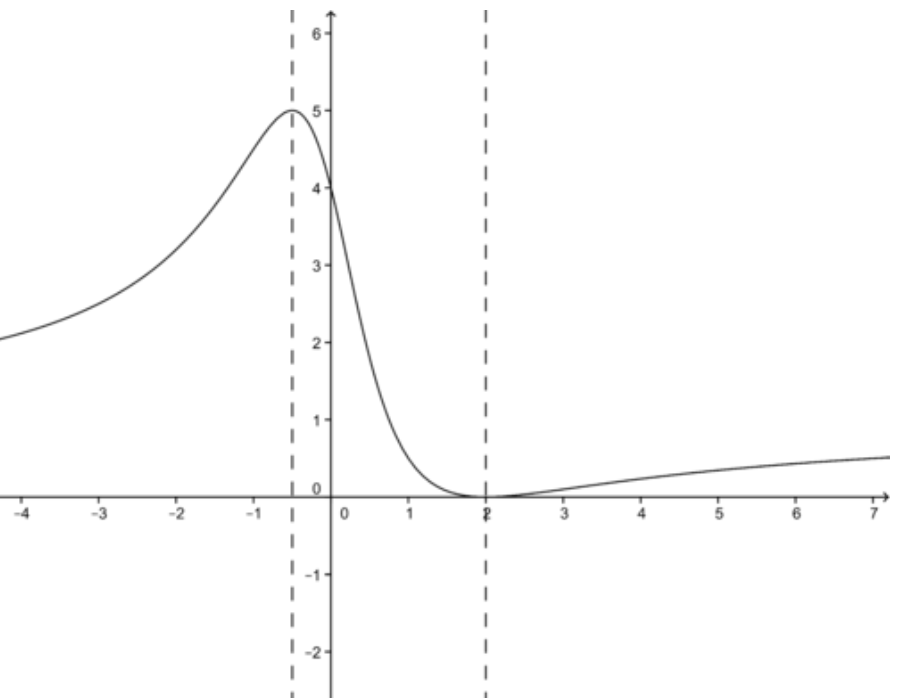
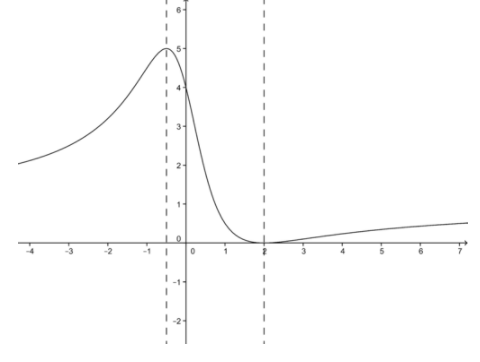
CC BY-NC-SA
Example 3
For the function \( f(x)=2x^4−3x^2+2 \nonumber\), find all critical values, classify each point as a relative maximum or a relative minimum, and identify any inflection points
The derivative is: \( f′(x)=8x^3−6x \nonumber\)
Which gives critical values: x=0 and \( x=± \frac{ \sqrt{3}}{2} \nonumber\)
The second derivative is: \( f′′(x)=24x^2−6 \nonumber\)
Evaluation at the critical points determines that f′′(0)<0, which means concave down (a maximum), and \( f′′(± \frac{\sqrt{3}}{2})>0 \nonumber\) means concave up (two minima).
The second derivative is 0 when \( 24x^2−6=6(2x−1)(2x+1)=0 \nonumber\).
x=0 and x=±12 are inflection points.
Review
For the #1-8, find the critical points, determine if each is a local minimum or maximum, and determine any points of inflection.
- \( f(x)=x^3−3x^2+1 \nonumber\)
- \( f(x)=x^4−2x^3−x+2 \nonumber\)
- \( f(x)=sin2x \nonumber\) on the interval \( [0,\frac{π}{2}] \nonumber\).
- \( f(x)=\frac{1}{x^2−x+2} \nonumber\)
- \( f(x)=2x^3−3x^2+6x \nonumber\)
- \( f(x)=x^3−12x+5 \nonumber\) in the interval [-5, 3]
- \( f(x)=x^5+20x+5 \nonumber\)
- \( f(x)=x2−5x+6, (-1, 3] \nonumber\)
- Find the absolute maximum and absolute minimum of \( f(x)=x^3−3x^2+2 \nonumber\) on the interval [0, 4].
For #10-15, find the critical points and local minima and maxima.
- \( f(x)=x^2e^{−x} \nonumber\)
- \( f(x)=\frac{x^2}{x−1} \nonumber\)
- \( f(x)=5e^{−x}+x^3 \nonumber\)
- \( f(x)=e^{−2x}+e^x \nonumber\)
- \( f(x)=3^xe^{−x} \nonumber\)
- \( f(x)=xtanx \nonumber\) on the interval \( [−π,π] \nonumber\).
Vocabulary
| Term | Definition |
|---|---|
| concavity | Concavity describes the behavior of the slope of the tangent line of a function such that concavity is positive if the slope is increasing, negative if the slope is decreasing, and zero if the slope is constant. |
| decreasing function | A decreasing function is one with a graph that goes down from left to right. |
| first derivative test | The first derivative test says that if f is a continuous function and that x=c is a critical value of f, then if f′ changes from positive to negative at x=c then f has a local maximum at x=c, if f′ changes from negative to positive at x=c then f has a local minimum at x=c, and if f′ does not change sign at x=c then f has neither a local maximum nor minimum at x=c. |
| increasing function | An increasing function is one with a graph that goes up from left to right. |
| inflection point | An inflection point is a point in the domain where concavity changes from positive to negative or negative to positive. |
| second derivative test | The second derivative test says that if f is a continuous function near c and c is a critical value of f, then if f′′(c)<0 then f has a relative maximum at x=c, if f′′(c)>0 then f has a relative minimum at x=c, and if f′′(c)=0 then the test is inconclusive and x=c may be a point of inflection. |





