7.4: Second Derivative Test
- Page ID
- 1215
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The derivative of a function curve at a point is the mathematical analogy to our visually determining if the function is increasing or decreasing at the point. But if you look at a function curve, you can also determine visually whether the tangent lines are getting more vertical or more horizontal over an interval. The visual recognition of this rate of change of the slope is a measure of curvature (or concavity), which in turn can tell you specifically what type of extrema are present. The mathematical representation of the rate of change of the slope is the second derivative, which is used to identify types of curvature. What is the relationship between the second derivative and the concavity?
Concavity and the Second Derivative Test
There is a property about the shape, or curvature, of a graph called concavity, which will help identify precisely the intervals where a function is either increasing or decreasing, where the maxima and minima are located, and also help to sketch the graph. Concavity is the direction in which the curve opens.
The type of concavity on a curve is defined as follows:
A function f is said to be concave upward on [a,b] contained in the domain of f if f′ is an increasing function on [a,b] and concave downward on [a,b] if f′ is a decreasing function on [a,b].
Here is a function that illustrates these properties.
Consider the function \( f(x)=x^3−x \nonumber\):
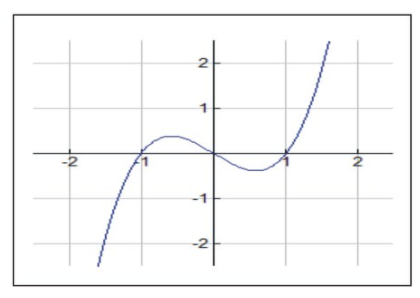
CC BY-NC-SA
Since \( f(x)=x^3−x=x(x^2−1) \nonumber\), the function has zeros at x=±1,0.
Also, \( f′(x)=0=3x^2−1 \nonumber\), tells us the location of extrema: a relative maximum at \( x=− \frac{ \sqrt{3}}{3} \nonumber\) and a relative minimum at \( x= \frac{ \sqrt{3}}{3} \nonumber\).
Note that the graph appears to be concave down for all intervals in (−∞,0) and concave up for all intervals in (0,+∞). Where do you think the concavity of the graph changed from concave down to concave up? If you answered at x=0 you would be correct.
In general, we wish to identify not only the extrema of a function but also the points where the graph changes concavity. A point on a graph of a function f where the concavity changes is called an inflection point.
The problem above had only one inflection point. But we can easily come up with examples of functions where there are more than one points of inflection.
Consider the function \( f(x)=x^4−3x^3+x−2 \nonumber\) shown in the figure.
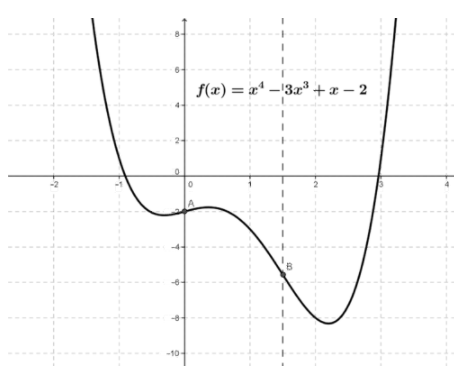
CC BY-NC-SA
We can see that the graph has two relative minimums, one relative maximum, and two inflection points (at A and B).
In general we can use the following test for concavity:
Suppose that f is continuous on [a,b] and that I is some open interval in the domain of f.
- If f′′(x)>0 for all x∈I, then the graph of f is concave upward on I
- If f′′(x)<0 for all x∈I, then the graph of f is concave downward on I
Let’s apply the concavity test to the function \( f(x)=x^4−3x^3+x−2 \nonumber\):
The second derivative is, \( f′′(x)=12x^2−18x=6x(2x−3) \nonumber\), and the concavity is given in the table.
|
Interval or Point |
f′′(x) |
Concavity |
|
[-1,0) |
>0 |
Upward |
|
0 |
=0 |
Change=Inflection |
|
(0, 1.5) |
<0 |
Downward |
|
1.5 |
=0 |
Change=Inflection |
|
(1.5, 3] |
>0 |
Upward |
Can you see how the concavity gives a clue to the presence of a relative maximum, or minimum, or inflection point? A consequence of the concavity test is the following test to identify where we have extrema and inflection points of f.
The Second Derivative Test for Extrema is as follows:
Suppose that f is a continuous function near c and that c is a critical value of f Then
- If f′′(c)<0, then f has a relative maximum at x=c.
- If f′′(c)>0, then f has a relative minimum at x=c.
- If f′′(c)=0, then the test is inconclusive and x=c may be a point of inflection.
Does the test work for our previous example of \( f(x)=x^4−3x^3+x−2 \nonumber\)?
We can find the critical values where \( f′(x)=4x^3−9x^2+1=0 \nonumber\), and use them to evaluate f′′(c). The results are shown below.
|
Critical Point |
f′′(c) |
Conclusion |
|
x=−0.312 |
>0 |
Relative Minimum |
|
x=0.364 |
<0 |
Relative Maximum |
|
x=2.198 |
>0 |
Relative Minimum |
The tests works on this function.
Remember, however, that the Second Derivative Test cautions us that if f′′(c)=0, the test is inconclusive, because c may be an inflection point. Recall that this was the case for \( f(x)=x^3 \nonumber\).
Examples
Example 1
Earlier, you were asked what relationship between the curvature of a function and the second derivative is. The curvature of a function graph can be described by its concavity (up or down), which in turn can be determined at each point by the second derivative (if it is defined). Because critical points can determine the locations of relative maxima or minima without identifying which, knowing the type of curvature from the second derivative can identify specifically whether we have a minimum or a maximum, or neither.
Example 2
Consider the function \( f(x)=x+ \frac{4}{x} \nonumber\). Find the critical points, and determine whether they are relative maximums or relative minimums by using the Second Derivative Test.
The first thing to notice is that the function is not defined at x=0.
To find the critical points we look for points c where f′(c)=0.
\) f′(x)=1− \frac{4}{x^2}=0 \nonumber\) means there are critical points at x=−2, and x=2.
Since \( f′′(x)= \frac{8}{x^3} :f′′(−2)=−1 \nonumber\) and the curve is concave downward with a relative maximum; f′′(2)=1, and the curve is concave upward with a relative minimum.
The function graph is as shown.
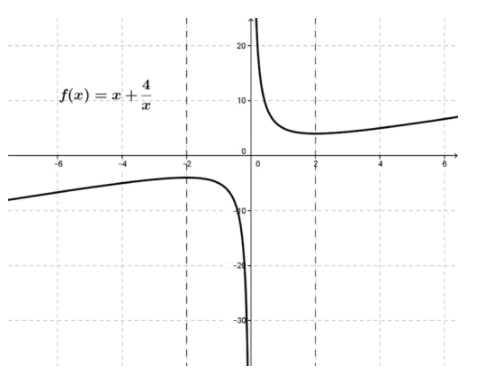
CC BY-NC-SA
Review
- Find all extrema using the Second Derivative Test: \( f(x)= \frac{x^2}{4}+ \frac{4}{x} \nonumber\).
- Consider \( f(x)= x^2+ax+b \nonumber\), with f(1)=3.
- Determine a and b so that x=1 is a critical value of the function f.
- Is the point (1, 3) a maximum, a minimum or neither?
For #3-6, find all extrema and inflection points. Sketch the graph.
- \( f(x)=x^3+x^2 \nonumber\)
- \( f(x)= \frac{x^2+3}{x} \nonumber\)
- \( f(x)=x^3−12x \nonumber\)
- \( f(x)=− \frac{1}{4}x^4+2x^2 \nonumber\)
- Use your graphing calculator to examine the graph of \( f(x)=x(x−1)^3 \nonumber\) (Hint: you will need to change the y range in the viewing window)
- Discuss the concavity of the graph in the interval \( (0, \frac{1}{2}) \nonumber\).
- Use your calculator to find the minimum value of the function in the interval.
- True or False: \( f(x)=x^4+4x^3 \nonumber\) has a relative minimum at x=−2 and a relative maximum at x=0?
- If possible, provide an example of a non-polynomial function that has exactly one relative minimum.
- If possible, provide an example of a non-polynomial function that is concave downward everywhere in its domain.
- Let f(x) be a continuous function and let [a,b] be a closed interval over which f(x) is defined. If we know that f(x) is positive over the interval [a,b], does this tell us anything about the concavity of f(x) over [a,b]?
- Is the function f(x)=x4 concave up or down over the interval [10, 11]?
- Is the function f(x)=−cos(x) concave up or down over the interval \( [ \frac{π}{2}, \frac{3π}{2}] \nonumber\)?
- If the first derivative of f(x) is \( f′(x)=20^xsin(π^x) \nonumber\), is f(x) concave up or down over the interval \( [0, \frac{1}{2}] \nonumber\)?
- What is an inflection point of the function \( f(x)=4x^3+3x^2+2x+1 \nonumber\)?
- Use the second derivative test to classify the extrema of the function \( f(x)=x^3+x^2−5ln(x) \nonumber\) over the interval \( (\frac{1}{2},2) \nonumber\).
- Use the second derivative test to classify the extrema of the function \( f(x)=5^{sin(x)} \nonumber\) over the interval \( (\frac{π}{4}, \frac{3π}{4}) \nonumber\).
- Use the second derivative test to classify the extrema of the function \( f(x)=ln(2x+x^2) \nonumber\) over the interval \( (−\frac{5}{2},− \frac{1}{2}) \nonumber\).
- Use the second derivative test to classify the extrema of the function \( f(x)=x^4 \nonumber\) over the interval (1, 5).
- Can we use the second derivative test to check if x=0 is a maximum or a minimum of the function \( f(x)=x^{10}+25 \nonumber\)?
Vocabulary
| Term | Definition |
|---|---|
| concave downward | A function f is said to be concave downward on [a,b] if f′ is a decreasing function on [a,b]. |
| concave upward | A function f is said to be concave upward on [a,b] contained in the domain of f if f′ is an increasing function on [a,b]. |
| concavity | Concavity describes the behavior of the slope of the tangent line of a function such that concavity is positive if the slope is increasing, negative if the slope is decreasing, and zero if the slope is constant. |
| inflection point | An inflection point is a point in the domain where concavity changes from positive to negative or negative to positive. |
| second derivative test | The second derivative test says that if f is a continuous function near c and c is a critical value of f, then if f′′(c)<0 then f has a relative maximum at x=c, if f′′(c)>0 then f has a relative minimum at x=c, and if f′′(c)=0 then the test is inconclusive and x=c may be a point of inflection. |

