9.2: Antiderivative

You have spent many lessons learning about how to find the derivative, f′(x), of a function f(x), and the process of differentiation. It should be no surprise then that there would be a name for the function f(x), or family of functions, that can generate f′(x) when differentiated: f(x) and f′(x) are a pair of inverse functions, and f(x) is called an antiderivative of f′(x). Before continuing with the lesson, try listing functions that are antiderivative and derivative pairs? 

---

The Antiderivative

Let’s start off and introduce the idea of the antiderivative of a function.

A function F(x) is called an antiderivative of a function f if F′(x)=f(x) for all x in the domain of f.

How is this definition used?

Consider the function \( f(x)=3x^2 \nonumber\).

Can you think of a function F(x) such that F′(x)=f(x)? You should be able to think of lots of them.

Since we differentiate F(x) to get f(x), we see that \( F(x)=x^3+C \nonumber\) will work for any constant C. Graphically, we can think of the set of all antiderivatives as vertical transformations of the graph of \( F(x)=x^3 \nonumber\). The figure shows two such transformations.

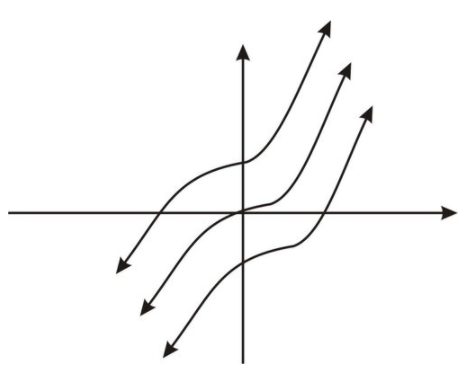
CC BY-NC-SA

With our definition and initial example, we now look to formalize the definition and develop some useful rules for computational purposes, and begin to see some applications.

Introduction to Indefinite Integrals

The process of finding antiderivatives is called antidifferentiation, more commonly referred to as integration. Here is how the integration is indicated and how it works:

F′(x)=f(x) ... Start with the differential equation that represents the definition of the antiderivative

\( \int F′(x)dx=\int f(x)dx \nonumber\) ... Invoke the integration (antidifferentiation) operation using the special symbol ∫.

\( F(x)+C= \int f(x)dx \nonumber\) ... Obtain the antiderivative F(x) and a constant of integration, C.

\( \int f(x)dx=F(x)+C \nonumber\) ... Note that if we differentiate both sides, we get back the original equation:

\[ \frac{d}{dx}[ \int f(x)dx]=f(x)=\frac{d}{dx}[F(x)+C]=F′(x) \nonumber\]

We refer to ∫f(x)dx as “the indefinite integral of f(x) with respect to x”. The function f(x) is called the integrand and the constant C is called the constant of integration. Finally the symbol dx indicates that we are to integrate with respect to x.

Using this notation, we would summarize the last example as follows:

\[ \int 3x^2dx=x^3+C \nonumber\]

Now, consider the function f(x)=cosx

Can you think of a function F(x) such that F′(x)=f(x)?

If you said F(x)=sinx+C you would be correct and here is how this would be written.

f(x)=F′(x) . . . Start with the differential equation that represents the definition of the antiderivative

cosx=F′(x) . . . Substitute for f(x)

\( \int cosx dx= \int F′(x)dx \nonumber\) . . . Invoke the integration (antidifferentiation) operation using the special symbol ∫.

\( \int cosx dx=F(x)+C \nonumber\) . . . Obtain the antiderivative F(x) and a constant of integration, C.

\( \int cosx dx=sinx+C \nonumber\) . . . We know F(x)=sinx because if we differentiate both sides, we get back the original equation.

We have looked at the derivatives of a number of functions through the calculus concepts and can put together a list of functions and their antiderivatives as shown below.

Summary of Basic Indefinite Integrals And Antiderivatives

Function f(x)	Antiderivative \( /int f(x)dx=F(x)+C \nonumber\)
1	x+C
x	\( \frac{x^2}{2}+C \nonumber\)
\( x^2 \nonumber\)	\( \frac{x^3}{3}+C \nonumber\)
\( x^n,\nonumber\) n≠−1	\( \frac{x^{n+1}}{n+1}+C \nonumber\)
\( \frac{1}{x} \nonumber\)	\( lnx+C \nonumber\)
sinx	−cosx+C
cosx	sinx+C
\( sec^2x \nonumber\)	tanx+C
\( csc^2x \nonumber\)	−cotx+C
secxtanx	secx+C
cscxcotx	−cscx+C
\( e^x \nonumber\)	\( e^x+C \nonumber\)
\( b^x \nonumber\) b>0	\( \frac{b^x}{lnb}+C \nonumber\)
\( \frac{1}{xlnb} \nonumber\)	\( log_bx+C \nonumber\)

As with differentiation, there are several rules for dealing with the sum and difference of integrable functions. 

Basic Integration Rules

If f and g are integrable functions, and C is a constant, then:

\[ \int [f(x)+g(x)]dx= \int f(x)dx+ \int g(x)dx \nonumber\],

\[ \int [f(x)−g(x)]dx= \int f(x)dx− \int g(x)dx \nonumber\],

\[ \int [Cf(x)]dx=C \int f(x)dx \nonumber\]

Compute the following indefinite integral.

\[ \int [2x^3+3x^2−1x]dx \nonumber\]

Using our rules we have

\[ \int [2x^3+3x^2−1x]dx=2 \int x^3dx+3 \int \frac{1}{x^2}dx− \int \frac{1}{x}dx \nonumber\]

\[ =2(\frac{x^4}{4})+3(\frac{x^{−1}}{−1})−lnx+C \nonumber\]

\[ =\frac{x^4}{2}−\frac{3}{x}−lnx+C \nonumber\].

Note that sometimes our rules need to be modified slightly due to operations with constants.

---

Examples

Example 1

Earlier, you were asked to try listing functions that are antiderivative and derivative pairs. By doing so you are presenting the results of differentiation and integration operations. If all you did was to list the function being differentiated as the antiderivative, this is correct. By now you have realized that there is a family of antiderivatives you could have chosen from, each differing by a constant of integration.

Example 2

Compute the following indefinite integral:

\[ \int e^{3x}dx \nonumber\].

We first note that our rule for integrating exponential functions does not work here since ddxe3x=3e3x. However, if we remember to divide the original function by the constant then we get the correct antiderivative and have

\[ \int e^{3x}dx=\frac{e^{3x}}{3}+C \nonumber\].

We can now re-state the rule in a more general form as

\[ \int e^{kx}dx= \frac{e^{kx}}{3}+C \nonumber\].

---

Review

For #1-6, find an antiderivative of the function

1. \( f(x)=1−3x^2−6x \nonumber\)
2. \( f(x)=x−x^\{frac{2}{3}} \nonumber\)
3. \( f(x)=(2x+1)^{\frac{1}{5}} \nonumber\)
4. \( f(x)=cosx−x \nonumber\)
5. \( f(x)=x^5−7x^2+2 \nonumber\)
6. \(f(x)=e^{−2x}+e^x \nonumber\)

For #7-12, find the indefinite integral

7. \( \int (2+\sqrt{5})dx \nonumber\]
8. \( \int 2(x−3)^3dx \nonumber\)
9. \( \int (x^2⋅x^\frac{1}{3})dx \nonumber\)
10. \( \int (x+\frac{1}{x^4\sqrt{x}})dx \nonumber\)
11. \( (cosx+2sinx)dx \nonumber\)
12. \( \int 2sinxcosxdx \nonumber\)
13. Solve the differential equation \( f′(x)=4x^3−3x^2+x−3 \nonumber\).
14. Find the antiderivative F(x) of the function \( f(x)=2e^{2x}+x−2 \nonumber\) that satisfies F(0)=5.
15. Evaluate the indefinite integral \( \int |x|dx \nonumber\) (Hint: Examine the graph of f(x)=|x|.)

---

Review (Answers)

To see the Review answers, open this PDF file and look for section 5.1. 

---

Vocabulary

Term	Definition
antiderivative	An antiderivative is a function that reverses a derivative. Function A is the antiderivative of function B if function B is the derivative of function A.
antidifferentiation	The process of finding antiderivatives is called antidifferentiation , more commonly referred to as integration.
constant of integration	The constant of integration is the constant C in the equation ∫f(x)dx=F(x)+C relating the function f(x) and the antiderivative F.
integrand	An integrand is the argument f(x) in the indefinite integral ∫f(x)dx.
integration	The process of finding antiderivatives is sometimes called antidifferentiation, but more commonly referred to as integration.

---

Additional Resources

PLIX: Play, Learn, Interact, eXplore - Antiderivative: Piecing it Together

Practice: Antiderivative

Real World: Rocky Mountain High