2.5: Inductive Reasoning from Patterns
- Page ID
- 2138
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Inductive Reasoning
One type of reasoning is inductive reasoning. Inductive reasoning entails making conclusions based upon examples and patterns. Visual patterns and number patterns provide good examples of inductive reasoning. Let’s look at some patterns to get a feel for what inductive reasoning is.
What if you were given a pattern of three numbers or shapes and asked to determine the sixth number or shape that fit that pattern?
Example \(\PageIndex{1}\)
A dot pattern is shown below. How many dots would there be in the \(4^{th}\) figure? How many dots would be in the \(6^{th}\) figure?
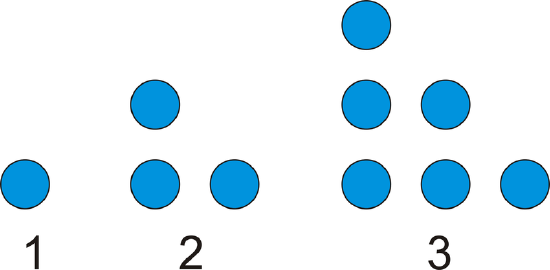Figure \(\PageIndex{1}\)Solution
Draw a picture. Counting the dots, there are \(4+3+2+1=10\) dots.
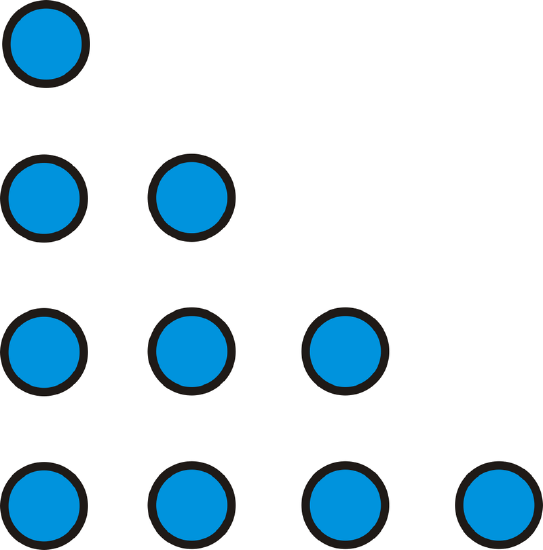Figure \(\PageIndex{2}\)For the \(6^{th}\) figure, we can use the same pattern, \(6+5+4+3+2+1\). There are 21 dots in the \(6^{th}\) figure.
Example \(\PageIndex{2}\)
How many triangles would be in the \(10^{th}\) figure?
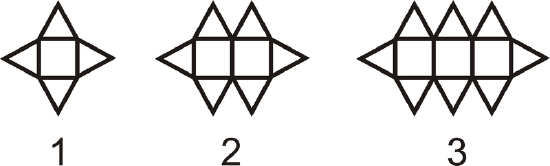Figure \(\PageIndex{3}\)Solution
There would be 10 squares in the \(10^{th}\) figure, with a triangle above and below each one. There is also a triangle on each end of the figure. That makes \(10+10+2=22\) triangles in all.
Example \(\PageIndex{3}\)
Look at the pattern \(2, 4, 6, 8, 10, \ldots\) What is the \(19^{th}\) term in the pattern?
Solution
Each term is 2 more than the previous term.
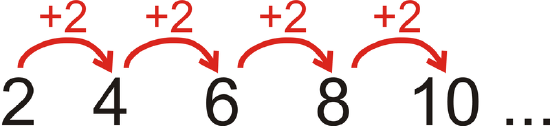Figure \(\PageIndex{4}\)You could count out the pattern until the \(19^{th}\) term, but that could take a while. Notice that the \(1^{st}\) term is \(2 \cdot 1\), the 2nd term is \(2 \cdot 2\), the 3rd term is \(2 \cdot 3\), and so on. So, the \(19^{th}\) term would be \(2 \cdot 19\) or 38.
Example \(\PageIndex{4}\)
Look at the pattern: \(3, 6, 12, 24, 48, \ldots\)
What is the next term in the pattern? What is the \(10^{th}\) term?
Solution
Each term is multiplied by 2 to get the next term.
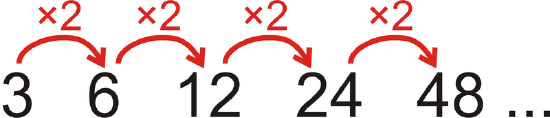Figure \(\PageIndex{5}\)Therefore, the next term will be \(48 \cdot 2\) or 96.
To find the \(10^{th}\) term, continue to multiply by 2, or \(3\cdot \underbrace{2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2 \cdot 2 }_{2^{9}}=1536\).
Example \(\PageIndex{5}\)
Find the 8th term in the list of numbers: \(2, \dfrac{3}{4}, \dfrac{4}{9}, \dfrac{5}{16}, \dfrac{6}{25}\ldots\)
Solution
First, change 2 into a fraction, or \(\dfrac{2}{1}\). So, the pattern is now \(\dfrac{2}{1}, \dfrac{3}{4}, \dfrac{4}{9}, \dfrac{5}{16}, \dfrac{6}{25}\ldots\) The top is \(2, 3, 4, 5, 6\). It increases by 1 each time, so the \(8^{th}\) term’s numerator is 9. The denominators are the square numbers, so the \(8^{th}\) term’s denominator is \(8^2\) or 64. The \(8^{th}\) term is \(\dfrac{9}{64}\).
Review
For questions 1-3, determine how many dots there would be in the \(4^{th}\) and the \(10^{th}\) pattern of each figure below.
-
Figure \(\PageIndex{6}\) -
Figure \(\PageIndex{7}\) -
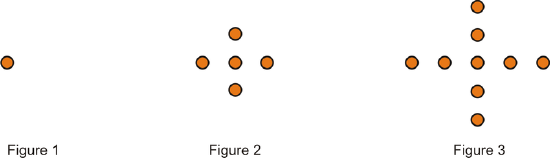Figure \(\PageIndex{8}\) - Use the pattern below to answer the questions.
Figure \(\PageIndex{9}\)- Draw the next figure in the pattern.
- How does the number of points in each star relate to the figure number?
- Use the pattern below to answer the questions. All the triangles are equilateral triangles.
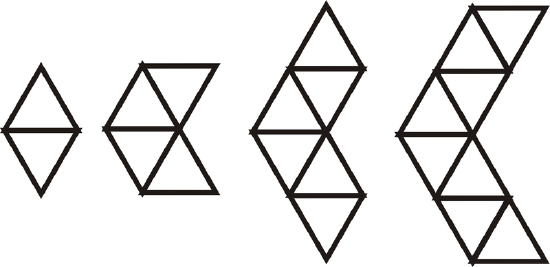Figure \(\PageIndex{10}\)- Draw the next figure in the pattern. How many triangles does it have?
- Determine how many triangles are in the \(24^{th}\) figure.
For questions 6-13, determine: the next three terms in the pattern.
- \(5, 8, 11, 14, 17, \ldots\)
- \(6, 1, -4, -9, -14, \ldots\)
- \(2, 4, 8, 16, 32, \ldots\)
- \(67, 56, 45, 34, 23, \ldots\)
- \(9, -4, 6, -8, 3, \ldots\)
- \(\dfrac{1}{2}, \dfrac{2}{3}, \dfrac{3}{4}, \dfrac{4}{5}, \dfrac{5}{6}, \ldots\)
- \(\dfrac{2}{3}, \dfrac{4}{7}, \dfrac{6}{11},\dfrac{8}{15}, \dfrac{10}{19},\ldots\)
- \(-1, 5, -9, 13, -17, \ldots\)
For questions 14-17, determine the next two terms and describe the pattern.
- \(3, 6, 11, 18, 27, \ldots\)
- \(3, 8, 15, 24, 35, \ldots\)
- \(1, 8, 27, 64, 125, \ldots\)
- \(1, 1, 2, 3, 5, \ldots\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 2.1.
Vocabulary
| Term | Definition |
|---|---|
| Inductive Reasoning | Inductive reasoning is a type of reasoning where one draws conclusions from patterns and previous examples. |
| Equilateral Triangle | An equilateral triangle is a triangle in which all three sides are the same length. |
Additional Resources
Interactive Element
Video: Inductive Reasoning
Activities: Inductive Reasoning from Patterns Discussion Questions
Study Aids: Types of Reasoning Study Guide
Practice: Inductive Reasoning from Patterns
Real World: The Science of Induction