6.6: Circle Area
- Page ID
- 2186
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Area of a Circle
To find the area of a circle, all you need to know is its radius. If r is the radius of a circle, then its area is \(A=\pi r^2\).
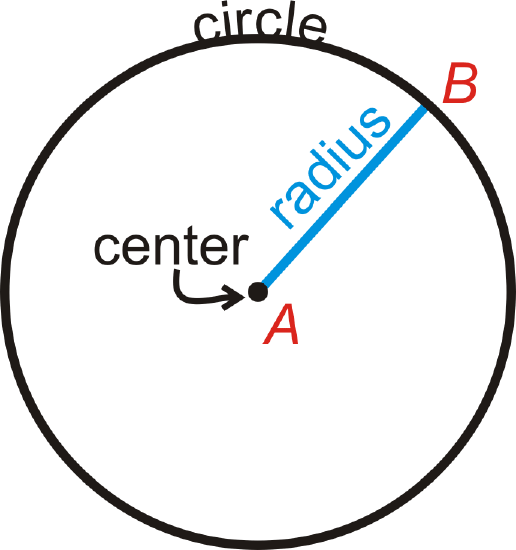
We will leave our answers in terms of \(\pi\), unless otherwise specified.
What if you were given the radius or diameter of a circle? How could you find the amount of space the circle takes up?
Example \(\PageIndex{1}\)
Find the area of a circle with a diameter of 12 cm.
Solution
If \(d=12\text{ cm }\), then \(r=6\text{ cm }\). The area is \(A=\pi (6^2)=36\pi \text{ cm }^2\).
Example \(\PageIndex{2}\)
If the area of a circle is \(20\pi \text{ units }\), what is the radius?
Solution
Plug in the area and solve for the radius.
\(\begin{aligned} 20\pi &=\pi r^2 \\ 20&=r^2 \\ r&=\sqrt{20}=2\sqrt{5}\text{ units } \end{aligned}\)
Example \(\PageIndex{3}\)
A circle is inscribed in a square. Each side of the square is 10 cm long. What is the area of the circle?
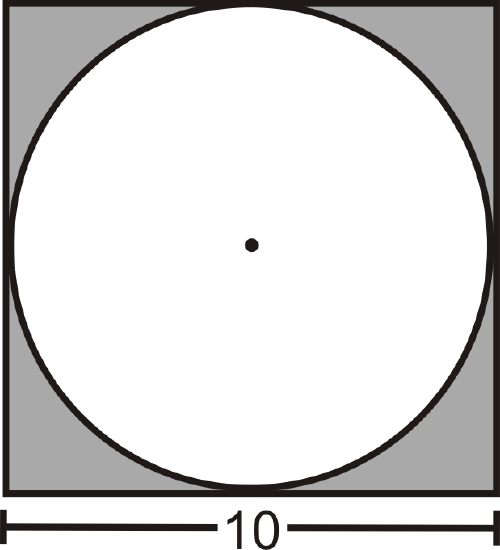
Solution
The diameter of the circle is the same as the length of a side of the square. Therefore, the radius is 5 cm.
\(A=\pi 5^2=25\pi \text{ cm }^2\)
Example \(\PageIndex{4}\)
Find the area of the shaded region from Example 3.
Solution
The area of the shaded region would be the area of the square minus the area of the circle.
\(A=102−25\pi =100−25\pi \approx 21.46\text{ cm }^2\)
Example \(\PageIndex{5}\)
Find the diameter of a circle with area \(36\pi \).
Solution
First, use the formula for the area of a circle to solve for the radius of the circle.
\(\begin{aligned}A&=\pi r^2 \\ 36\pi &=\pi r^2 \\ 36&=r^2 \\ r&=6\end{aligned}\)
If the radius is 6 units, then the diameter is 12 units.
Review
Fill in the following table. Leave all answers in terms of \(\pi\).
| radius | Area | circumference | |
|---|---|---|---|
| 1. | 2 | ||
| 2. | \(16\pi\) | ||
| 3. | \(10\pi\) | ||
| 4. | \(24\pi\) | ||
| 5. | 9 | ||
| 6. | \(90\pi\) | ||
| 7. | \(35\pi\) | ||
| 8. | \(7\pi\) | ||
| 9. | 60 | ||
| 10. | 36 |
Find the area of the shaded region. Round your answer to the nearest hundredth.
-
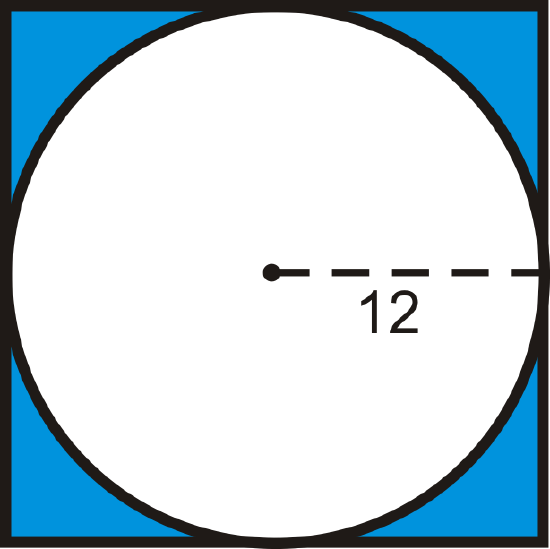
Figure \(\PageIndex{3}\) -
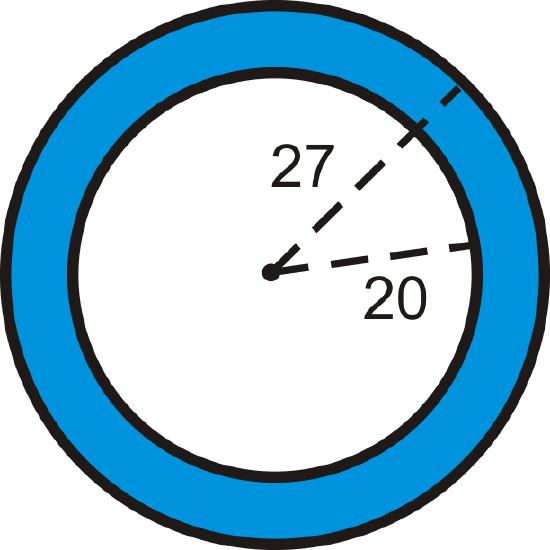
Figure \(\PageIndex{4}\) -
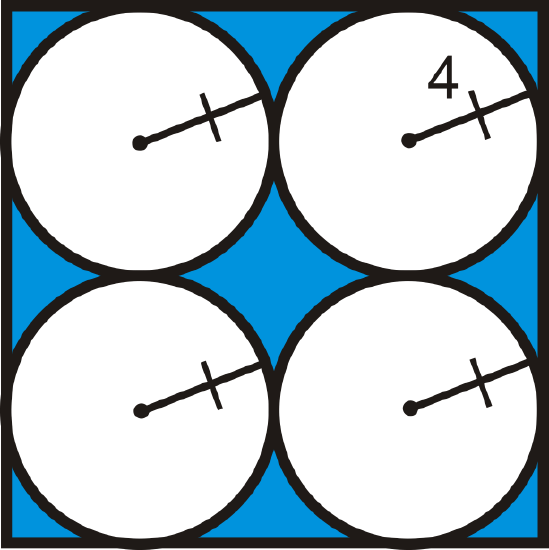
Figure \(\PageIndex{5}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 10.10.
Vocabulary
| Term | Definition |
|---|---|
| chord | A line segment whose endpoints are on a circle. |
| circle | The set of all points that are the same distance away from a specific point, called the center. |
| circumference | The distance around a circle. |
| diameter | A chord that passes through the center of the circle. The length of a diameter is two times the length of a radius. |
| pi | (or \(\pi\) ) The ratio of the circumference of a circle to its diameter. |
| radius | The distance from the center to the outer rim of a circle. |
Additional Resources
Interactive Element
Video: Determine the Area of a Circle
Activities: Area of a Circle Discussion Questions
Study Aids: Circumference and Arc Length Study Guide
Practice: Circle Area
Real World: Ringside Seats

