6.18: Tangent Lines
- Page ID
- 5043
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lines perpendicular to the radius drawn to the point of tangency.
Tangent Line Theorems
There are two important theorems about tangent lines.
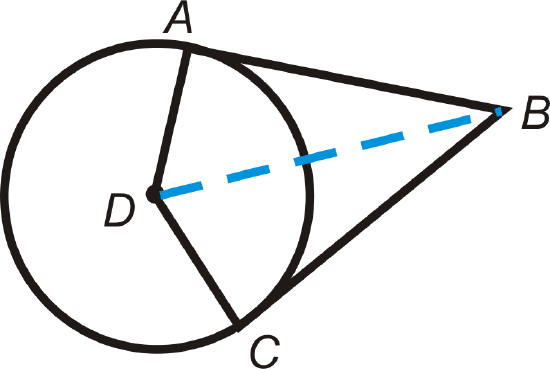
1. Tangent to a Circle Theorem: A line is tangent to a circle if and only if the line is perpendicular to the radius drawn to the point of tangency.
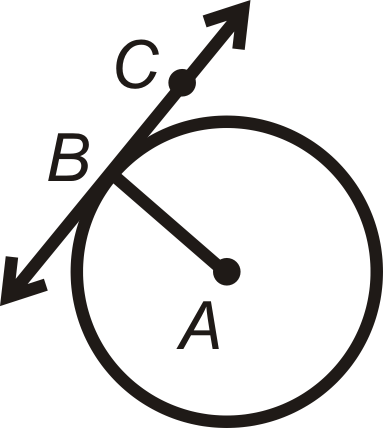
\(\overleftrightarrow{BC}\) is tangent at point \(B\) if and only if \(\overleftrightarrow{BC}\perp \overline{AB}\).
This theorem uses the words “if and only if,” making it a biconditional statement, which means the converse of this theorem is also true.
2. Two Tangents Theorem: If two tangent segments are drawn to one circle from the same external point, then they are congruent.
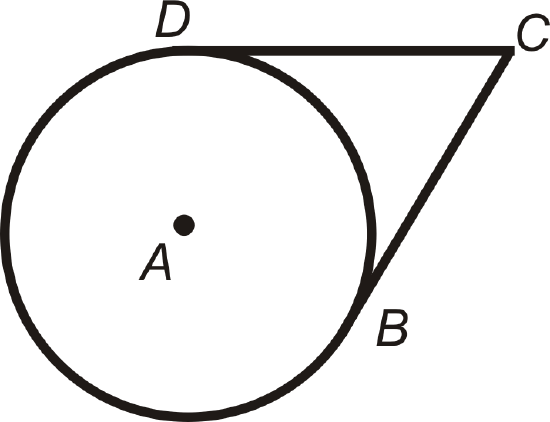
\(\overline{BC}\) and \(\overline{DC}\) have \(C\) as an endpoint and are tangent; \(\overline{BC}\cong \overline{DC}\).
What if a line were drawn outside a circle that appeared to touch the circle at only one point? How could you determine if that line were actually a tangent?
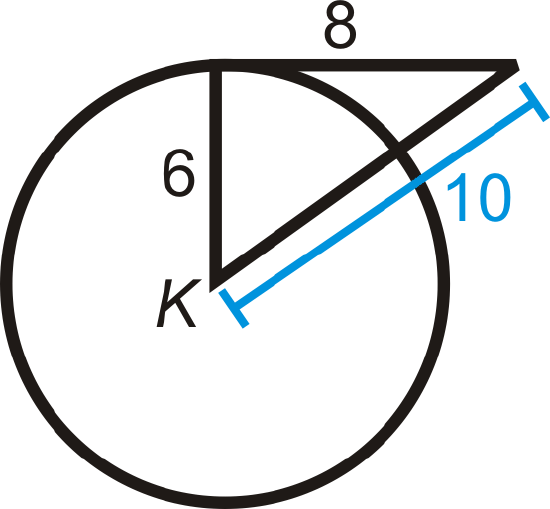
Example \(\PageIndex{1}\)
Determine if the triangle below is a right triangle.
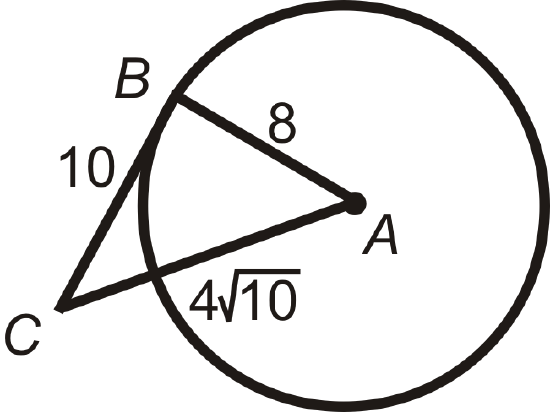
Solution
Use the Pythagorean Theorem. \(4\sqrt{10}\) is the longest side, so it will be \(c\).
Does
\(\begin{aligned} 8^2+10^2&= (4\sqrt{10})^2? \\ 64+100&\neq 160\end{aligned}\)
\(\Delta ABC\) is not a right triangle. From this, we also find that \(\overline{CB}\) is not tangent to \(\bigodot A\).
Example \(\PageIndex{2}\)
If \(D\) and \(C\) are the centers and \(AE\) is tangent to both circles, find \(DC\).
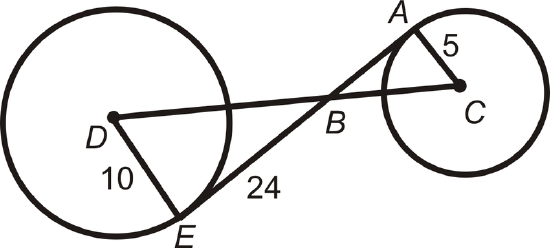
Solution
\(\overline{AE}\perp \overline{DE}\) and \(\overline{AE}\perp \overline{AC}\) and \(\Delta ABC \sim \Delta DBE\) by AA Similarity.
To find \(DB\), use the Pythagorean Theorem.
\(\begin{aligned} 10^2+24^2&=DB^2 \\ 100+576&=676 \\ DB&=\sqrt{676}=26 \end{aligned}\)
To find \(BC\), use similar triangles.
\(\dfrac{5}{10}=\dfrac{BC}{26}\rightarrow BC=13. \: DC=DB+BC=26+13=39\)
Example \(\PageIndex{3}\)
\(\overline{CB}\) is tangent to \(\bigodot A\) at point \(B\). Find \(AC\). Reduce any radicals.
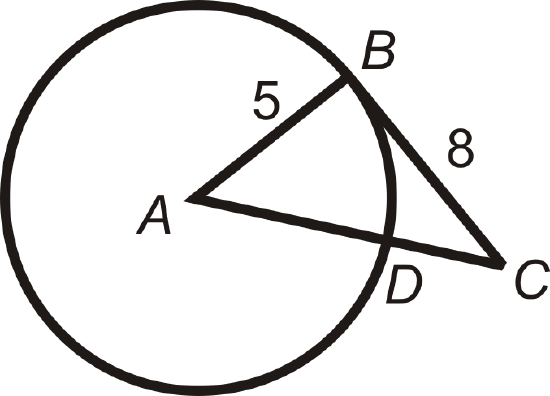
Solution
\(\overline{CB}\) is tangent, so \(\overline{AB}\perp \overline{CB}\) and \(\Delta ABC\) a right triangle. Use the Pythagorean Theorem to find \(AC\).
\(\begin{aligned} 5^2+8^2&=AC^2 \\ 25+64&=AC^2 \\ 89&=AC^2 \\ AC&=\sqrt{89}\end{aligned}\)
Example \(\PageIndex{4}\)
Using the answer from Example A above, find \(DC\) in \(\bigodot A\). Round your answer to the nearest hundredth.
Solution
\(\begin{aligned} DC&=AC−AD \\ DC&=\sqrt{89}−5 \approx 4.43 \end{aligned}\)
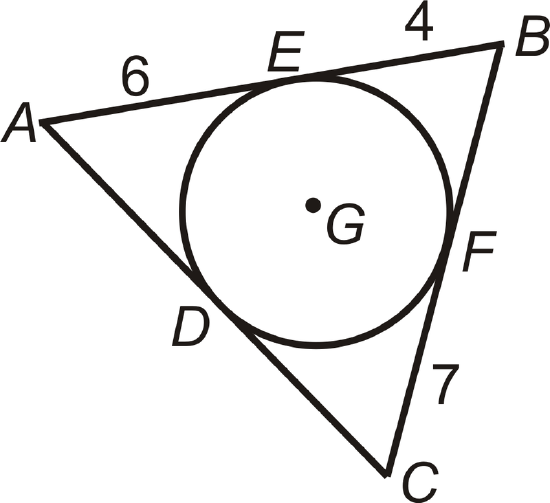
Example \(\PageIndex{5}\)
Find the perimeter of \(\Delta ABC\).
Solution
\(AE=AD\), \(EB=BF\), and \(CF=CD\). Therefore, the perimeter of
\(\Delta ABC=6+6+4+4+7+7=34\).
\(\bigodot G\) is inscribed in \(\Delta ABC\). A circle is inscribed in a polygon if every side of the polygon is tangent to the circle.
Review
Determine whether the given segment is tangent to \(\bigodot K\).
-
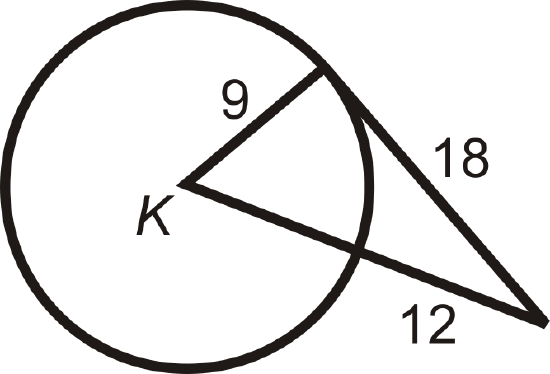
Figure \(\PageIndex{8}\) -
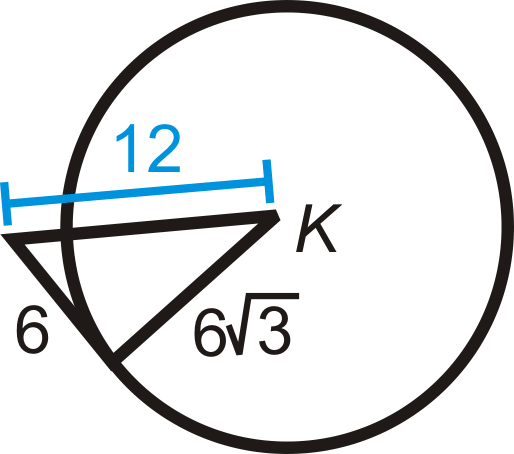
Figure \(\PageIndex{9}\) -
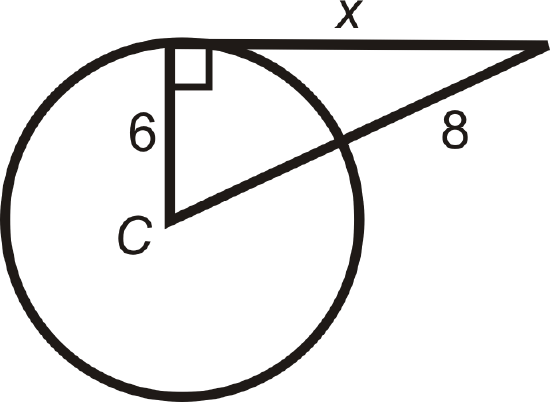
Figure \(\PageIndex{10}\)
Find the value of the indicated length(s) in \(\bigodot C\). \(A\) and \(B\) are points of tangency. Simplify all radicals.
-
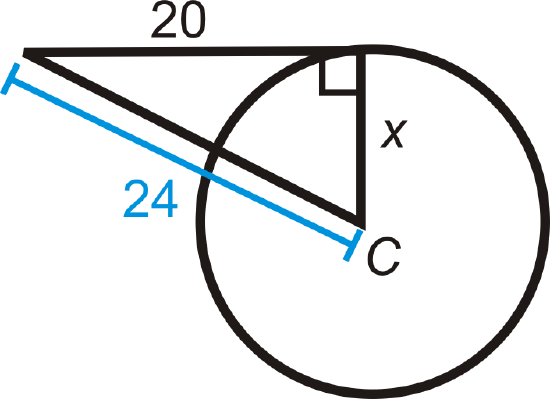
Figure \(\PageIndex{11}\) -
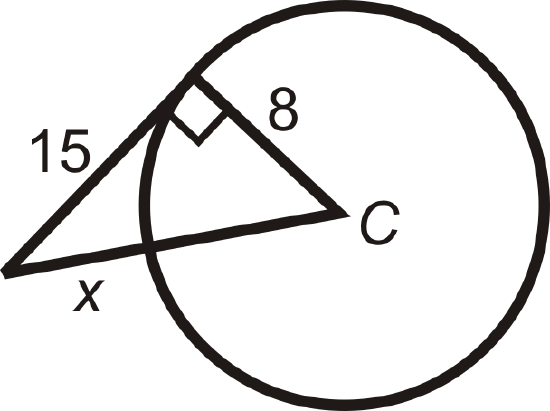
Figure \(\PageIndex{12}\) -
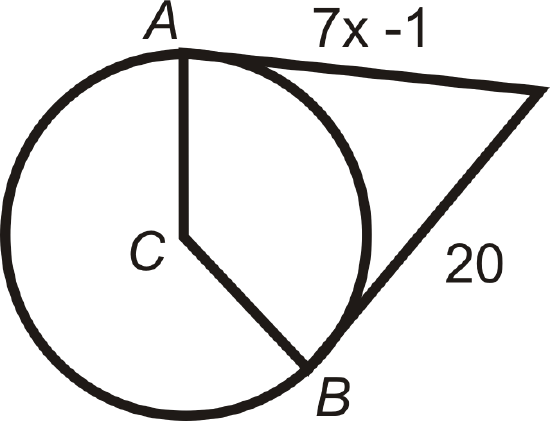
Figure \(\PageIndex{13}\) -
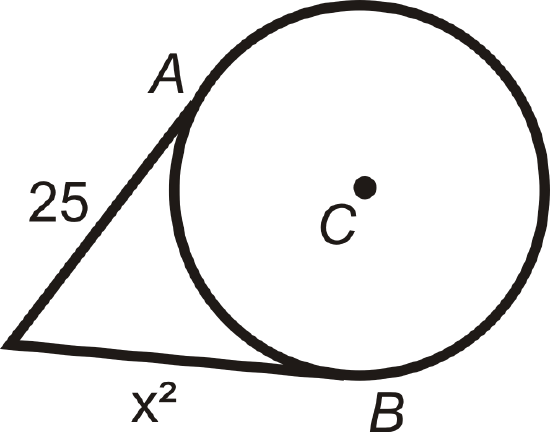
Figure \(\PageIndex{14}\) -
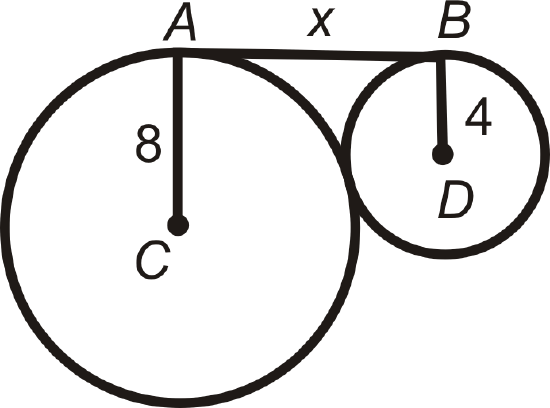
Figure \(\PageIndex{15}\) -
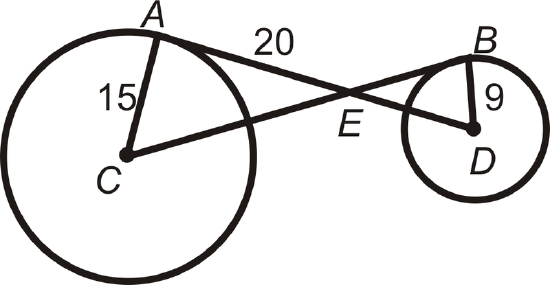
Figure \(\PageIndex{16}\)
\(A\) and \(B\) are points of tangency for \(\bigodot C\) and \(\bigodot D\).
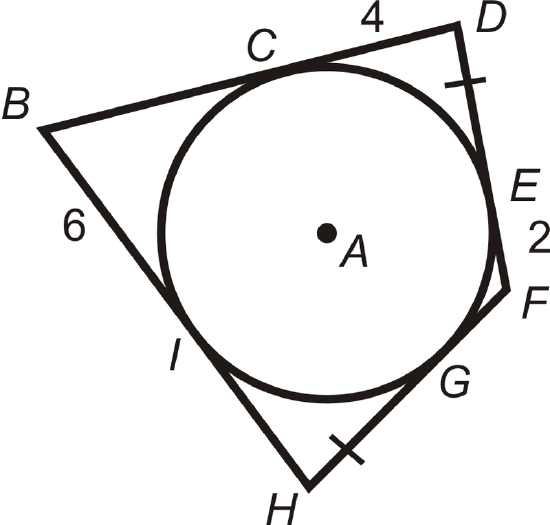
- Is \(\Delta AEC \sim \Delta BED\)? Why?
- Find \(CE\).
- Find \(BE\).
- Find \(ED\).
- Find \(BC\) and \(AD\).
\(\bigodot A\) is inscribed in \(BDFH\).
- Find the perimeter of \(BDFH\).
- What type of quadrilateral is \(BDFH\)? How do you know?
- Draw a circle inscribed in a square. If the radius of the circle is 5, what is the perimeter of the square?
- Can a circle be inscribed in a rectangle? If so, draw it. If not, explain.
- Draw a triangle with two sides tangent to a circle, but the third side is not.
- Can a circle be inscribed in an obtuse triangle? If so, draw it. If not, explain.
- Fill in the blanks in the proof of the Two Tangents Theorem.
Given: \(\overline{AB}\) and \(\overline{CB}\) with points of tangency at \(A\) and \(C\). \(\overline{AD}\) and \(\overline{DC}\) are radii.
Prove: \(\overline{AB}\cong \overline{CB}\)
| Statement | Reason |
|---|---|
| 1. | 1. |
| 2. \(\overline{AD}\cong \overline{DC}\) | 2. |
| 3. \(\overline{DA}\perp \overline{AB}\) and \(\overline{DC}\perp \overline{CB}\) | 3. |
| 4. | 4. Definition of perpendicular lines |
| 5. | 5. Connecting two existing points |
| 6. \(\Delta ADB\) and \(\Delta DCB\) are right triangles | 6. |
| 7.\(\overline{DB}\cong\overline{DB}\) | 7. |
| 8.\(\Delta ABD\cong \Delta CBD\) | 8. |
| 9.\(\overline{AB}\cong \overline{CB}\) | 9. |
- Fill in the blanks, using the proof from #21.
- \(ABCD\) is a _____________ (type of quadrilateral).
- The line that connects the ___________ and the external point \(B\) __________ \(\angle ABC\).
- Points \(A\), \(B\), and \(C\) are points of tangency for the three tangent circles. Explain why \(\overline{AT}\cong \overline{BT}\cong \overline{CT}\).
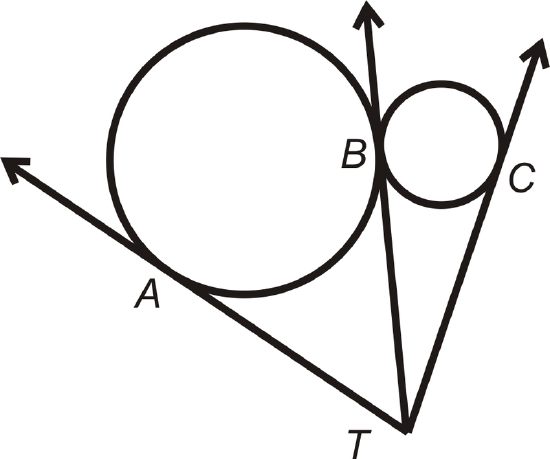
Figure \(\PageIndex{19}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 9.2.
Resources
Vocabulary
| Term | Definition |
|---|---|
| circle | The set of all points that are the same distance away from a specific point, called the center. |
| diameter | A chord that passes through the center of the circle. The length of a diameter is two times the length of a radius. |
| point of tangency | The point where the tangent line touches the circle. |
| radius | The distance from the center to the outer rim of a circle. |
| Tangent | The tangent of an angle in a right triangle is a value found by dividing the length of the side opposite the given angle by the length of the side adjacent to the given angle. |
| Tangent to a Circle Theorem | A line is tangent to a circle if and only if the line is perpendicular to the radius drawn to the point of tangency. |
| Two Tangent Theorem | The Two-Tangent Theorem states that if two tangent segments are drawn to one circle from the same external point, then they are congruent. |
Additional Resources
Interactive Element
Video: Tangent Lines Principles - Basic
Activities: Tangent Lines Discussion Questions
Study Aids: Properties of a Circle Study Guide
Practice: Tangent Lines
Real World: Swing Rides

