6.4: Circumference
- Page ID
- 2181
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Find the circumference of a circle using the formulas: \(C = \pi d\); \(C = 2\pi r\).
Circumference is the distance around a circle. The circumference can also be called the perimeter of a circle. However, we use the term circumference for circles because they are round.
Circumference Formula: \(C=\pi d\) where the diameter \(d=2r\), or twice the radius. So \(C=2\pi r\) as well.
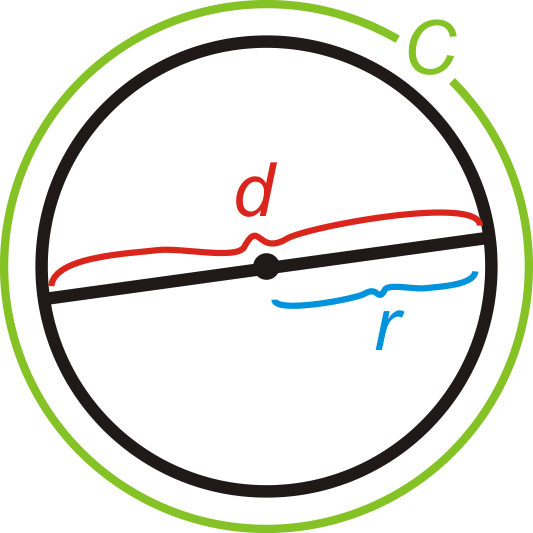
\(\pi\), or “pi” is the ratio of the circumference of a circle to its diameter. It is approximately equal to 3.14159265358979323846...
You should have a \pi button on your calculator. If you don't, you can use 3.14 as an approximation for \(\pi\). You can also leave your answers in terms of \(\pi\) for many problems.
What if you were given the radius or diameter of a circle? How could you find the distance around that circle?
Example \(\PageIndex{1}\)
Find the circumference of a circle with a radius of 7 cm.
Solution
Plug the radius into the formula.
\(C=2\pi (7)=14\pi \approx 44\text{ cm }\)
Example \(\PageIndex{2}\)
The circumference of a circle is \(64\pi\) units. Find the diameter.
Solution
Again, you can plug in what you know into the circumference formula and solve for \(d\).
\(\begin{aligned} 64\pi =\pi d \\ 64\text{ units }=d\end{aligned}\)
Example \(\PageIndex{3}\)
A circle is inscribed in a square with 10 in. sides. What is the circumference of the circle? Leave your answer in terms of \(\pi\).
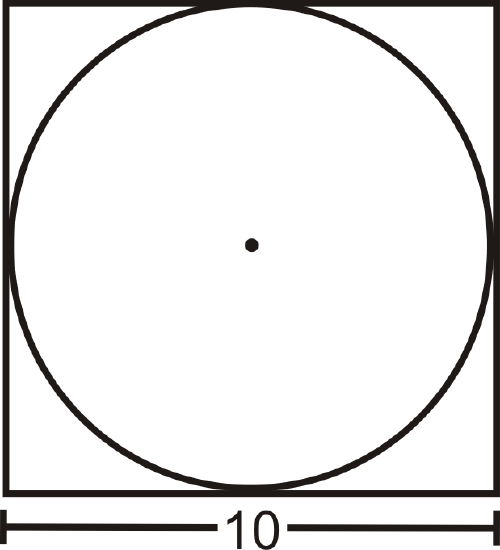
Solution
From the picture, we can see that the diameter of the circle is equal to the length of a side. \(C=10\pi \text{ in. }\)
Example \(\PageIndex{4}\)
Find the perimeter of the square in Example 3. Is it more or less than the circumference of the circle? Why?
Solution
The perimeter is \(P=4(10)=40\text{ in. }\) In order to compare the perimeter with the circumference we should change the circumference into a decimal.
\(C=10\pi \approx 31.42 \text{ in. }\) This is less than the perimeter of the square, which makes sense because the circle is inside the square.
Example \(\PageIndex{5}\)
The tires on a compact car are 18 inches in diameter. How far does the car travel after the tires turn once? How far does the car travel after 2500 rotations of the tires?
Solution
One turn of the tire is the circumference. This would be \(C=18\pi \approx 56.55\text{ in. }\) 2500 rotations would be \(2500\cdot 56.55\) in approx 141,375 in, 11,781 ft, or 2.23 miles.
Review
Fill in the following table. Leave all answers in terms of \(\pi\).
| diameter | radius | circumference | |
|---|---|---|---|
| 1. | 15 | ||
| 2. | 4 | ||
| 3. | 6 | ||
| 4. | \(84\pi\) | ||
| 5. | 9 | ||
| 6. | \(25\pi\) | ||
| 7. | \(2\pi\) | ||
| 8. | 36 |
- Find the circumference of a circle with \(d=\dfrac{20}{\pi} \text{ cm }\).
Square \(PQSR\) is inscribed in \(\bigodot T\). \(RS=8\sqrt{2}\).
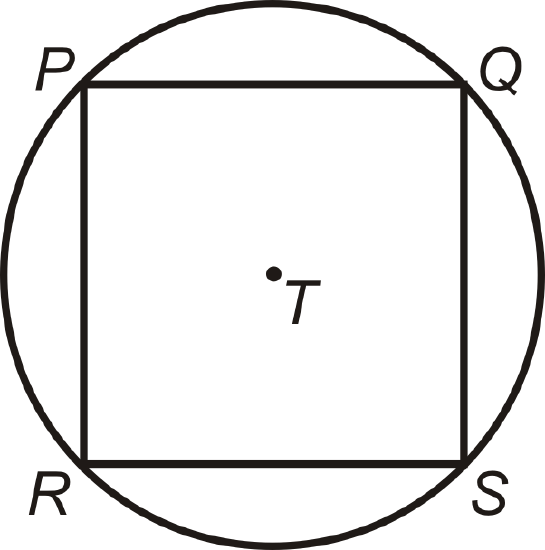
- Find the length of the diameter of \(\bigodot T\).
- How does the diameter relate to \(PQSR\)?
- Find the perimeter of \(PQSR\).
- Find the circumference of \(\bigodot T\).
For questions 14-17, a truck has tires with a 26 in diameter.
- How far does the truck travel every time a tire turns exactly once? What is this the same as?
- How many times will the tire turn after the truck travels 1 mile? (1 mile = 5280 feet)
- The truck has travelled 4072 tire rotations. How many miles is this?
- The average recommendation for the life of a tire is 30,000 miles. How many rotations is this?
Vocabulary
| Term | Definition |
|---|---|
| chord | A line segment whose endpoints are on a circle. |
| circle | The set of all points that are the same distance away from a specific point, called the center. |
| Circumference | The circumference of a circle is the measure of the distance around the outside edge of a circle. |
| diameter | A chord that passes through the center of the circle. The length of a diameter is two times the length of a radius. |
| pi | (or \(\pi\) ) The ratio of the circumference of a circle to its diameter. |
| Radius | The radius of a circle is the distance from the center of the circle to the edge of the circle. |
| Congruent | Congruent figures are identical in size, shape and measure. |
| Regular Polygon | A regular polygon is a polygon with all sides the same length and all angles the same measure. |
Additional Resources
Interactive Element
Video: Circumference of a Circle
Activities: Circumference Discussion Questions
study Aids: Circumference and Arc Length Study Guide
Practice: Circumference
Real World: A Roundabout Way Home