6.3: Use Diameter, Radius and Pi
- Page ID
- 2180
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Identify the constant ratio \(\pi= \dfrac{C}{d}\).
Pi

Carla has to go to the store and get a tablecloth for the round table in the dining room. In order to get the right size tablecloth, she needs to know the distance from one side of the table to the other side. The 3-foot long yardstick she has can only measure up to the center of the table, or halfway across. How can Carla figure out the distance across the circular table with only the yardstick and then use that information to find out the circumference of the table?
In this concept, you will learn the relationship between diameter and radius and identify pi as the ratio of diameter to circumference in a circle.
Circle Relationships
To work with circles, you need to know the different parts of a circle and how these key parts are measured.
You can measure the distance across the center of the circle. This distance is called the diameter of the circle.
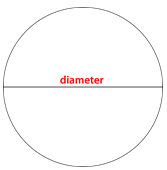
You can measure the distance from the center of the circle to the outer edge. This distance is called the radius.
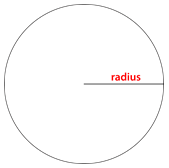
Notice that the radius is one-half of the measure of the diameter.
You can measure the perimeter of the circle too. This distance is called the circumference of the circle.
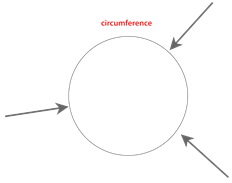
Archimedes, a mathematician in ancient Greece, is credited with figuring out the relationship between the diameter and circumference of a circle. Archimedes discovered that if you take the distance across the circle (diameter) and stretch it around the circumference, it would take a little over 3 lengths of the diameter to go around the circumference of the circle.
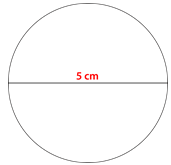
Let’s say that the diameter of this circle is 5 cm, in that case the circumference of the circle is three and a little more times the 5 cm, or a little less than 16 cm.
The ratio of the diameter to the circumference is called pi, \(\pi\). The numerical value of pi is a non-terminating decimal, which means it cannot be written precisely as a numeral since the decimal places never end or form a pattern. So, the number 3.14 is used to represent pi and is used for estimating the circumference of a circle.
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Carla and her trouble measuring the diameter of the round table.
Carla was still debating how to find the diameter of the round table when her mother walked in the dining room. When Carla explained the problem to her mom, her mom told her if the 3-foot long yardstick measured the distance from the edge of the table to the center point, then that was the radius of the table. Knowing the radius of the table was 3 feet, Carla knew she could use the relationship formula for radius and diameter to figure out the distance from one side of the table to the other.
Solution
First, Carla substituted the given measurement in the formula for diameter and radius.
\(\begin{aligned} 2 (\text{ radius })=\text{ diameter } \\ 2 (3\text{ feet })=\text{ diameter }\end{aligned}\)
Next, she multiplied 2 times 3.
\(6\text{ feet }= \text{ diameter }\)
The table’s diameter is 6 feet.
Carla could use this information to figure out the circumferences of the table by multiplying the diameter and pi (3.14).
Example \(\PageIndex{2}\)
Use the given value for the radius to find the diameter.
If the radius of a circle is 3, what is the diameter?
Solution
First, note the definition of radius and diameter. The radius is one-half the diameter or the diameter is twice the length of the radius.
\(2 (\text{ radius })=\text{ diameter }\)
Next, multiply the radius by 2 to get 6.
\(2(3)=6\)
The answer is 6.
Example \(\PageIndex{3}\)
If a circle has a diameter of 14 inches, what is its radius?
Solution
First, substitute the given measurement in the formula for diameter and radius.
\(\begin{aligned} 2 (\text{ radius })&=\text{ diameter }\\ 2r&=14 \text{ inches }\end{aligned}\)
Next, divide both sides by 2.
\(\begin{aligned}\dfrac{2r}{2}&=\dfrac{14}{2} \\ r&=7 \end{aligned}\)
The answer is 7.
Example \(\PageIndex{4}\)
If a circle has a radius of 11 inches, what is its diameter?
Solution
First, substitute the given measurement in the formula for diameter and radius.
\(\begin{aligned}2(\text{ radius })=\text{ diameter } \\ 2(11\text{ inches })=\text{ diameter } \end{aligned}\)
Next, multiply 2 and 11.
\(22=\text{ diameter }\)
The answer is 22.
Example \(\PageIndex{5}\)
If a circle has a diameter of 18 inches, what is its radius?
Solution
First, substitute the known values in the equation.
\(2(r)=18\)
Next, do the math and divide both sides by 2.
\(\begin{aligned}\dfrac{2r}{2}&=\dfrac{18}{2} \\ r&=9\end{aligned}\)
The answer is 9.
Review
Given each radius, determine the diameter.
- \(r=4\text{ in. }\)
- \(r=6\text{ in. }\)
- \(r=5\text{ in. }\)
- \(r=12\text{ in. }\)
- \(r=16\text{ ft. }\)
- \(r=28\text{ mm. }\)
- \(r=12.5\text{ ft. }\)
- \(r=1.25\text{ m. }\)
Given each diameter, determine the radius.
- \(d=12\text{ m. }\)
- \(d=18\text{ m. }\)
- \(d=12.5\text{ in. }\)
- \(d=18.5\text{ ft. }\)
- \(d=9.8\text{ in. }\)
- \(d=1.45\text{ mm. }\)
- \(d=1.75\text{ ft. }\)
- \(d=2.5\text{ ft. }\)
- \(d=221.25\text{ m. }\)
Vocabulary
| Term | Definition |
|---|---|
| \pi | \(\pi\) (Pi) is the ratio of the circumference of a circle to its diameter. It is an irrational number that is approximately equal to 3.14. |
| Archimedes | Archimedes was a Greek mathematician and philosopher. Among many other things, he identified 3.14 as pi. |
| Circumference | The circumference of a circle is the measure of the distance around the outside edge of a circle. |
| Diameter | Diameter is the measure of the distance across the center of a circle. The diameter is equal to twice the measure of the radius. |
| Pi | \(\pi\) (Pi) is the ratio of the circumference of a circle to its diameter. It is an irrational number that is approximately equal to 3.14. |
| Radius | The radius of a circle is the distance from the center of the circle to the edge of the circle. |
Interactive Element
Video: Circles: Radius, Diameter and Circumference
Practice: Use Diameter, Radius and Pi

