6.2: Identify Circle Components
- Page ID
- 2179
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Components, circumference, and area of circles.
Parts of Circles
Circles
A circle is the set of all points in the plane that are the same distance away from a specific point, called the center. The center of the circle below is point A. We call this circle “circle A,” and it is labeled \(\bigodot A\).
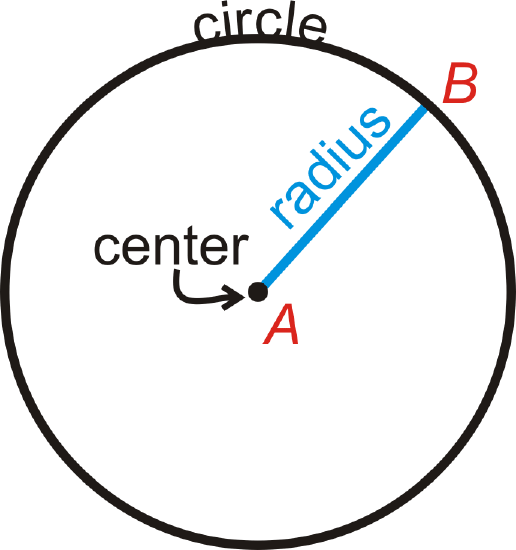
Important Circle Parts
Radius: The distance from the center of the circle to its outer rim.
Chord: A line segment whose endpoints are on a circle.
Diameter: A chord that passes through the center of the circle. The length of a diameter is two times the length of a radius.
Secant: A line that intersects a circle in two points.
Tangent: A line that intersects a circle in exactly one point.
Point of Tangency: The point where a tangent line touches the circle.
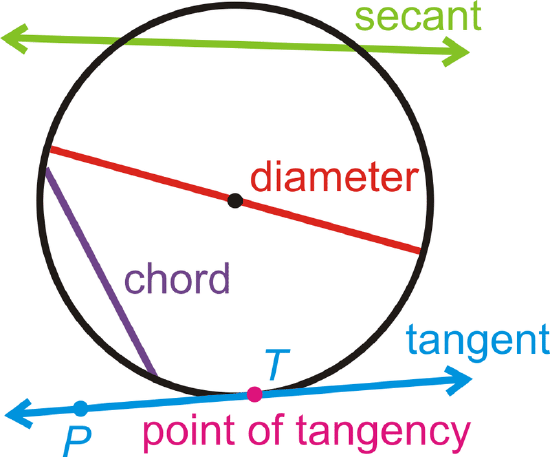
The tangent ray \(\overrightarrow{TP}\) and tangent segment \(\overline{TP}\) are also called tangents.
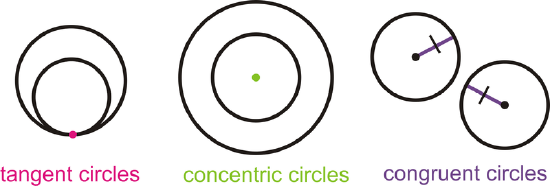
Tangent Circles: Two or more circles that intersect at one point.
Concentric Circles: Two or more circles that have the same center, but different radii.
Congruent Circles: Two or more circles with the same radius, but different center
What if you drew a line through a circle from one side to the other that does not pass through the center? What if you drew a line outside a circle that touched the circle at one point? What would you call these lines you drew?
Example \(\PageIndex{1}\)
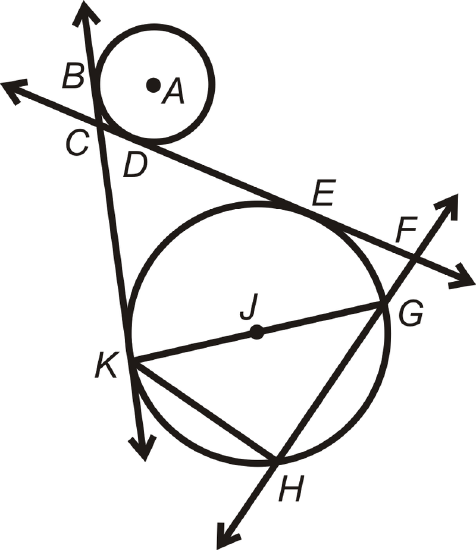
Find the parts of \(\bigodot A\) that best fit each description.
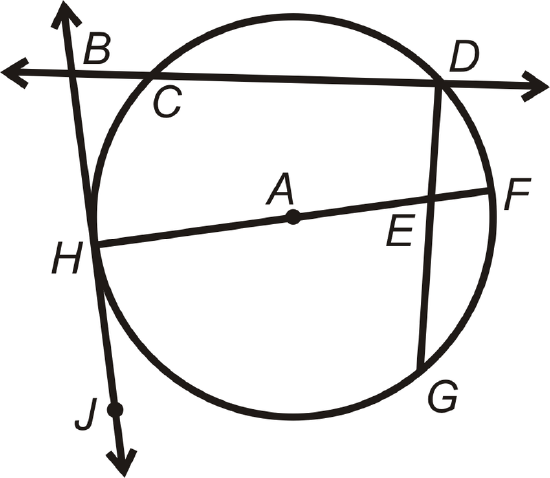
- A radius
- A chord
- A tangent line
- A point of tangency
- A diameter
- A secant
Solution
- \overline{HA}\) or \overline{AF}\)
- \(\overline{CD}\), \(\overline{HF}\), or \overline{DG}\)
- \(\overleftrightarrow{BJ}\)
- \(Point H\)
- \(\overline{HF}\)
- \(\overleftrightarrow{BD}\)
Example \(\PageIndex{2}\)
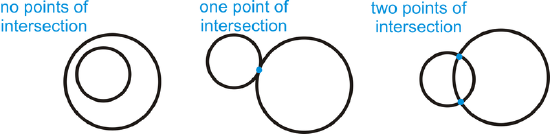
Draw an example of how two circles can intersect with no, one and two points of intersection. You will make three separate drawings.
Solution
Example \(\PageIndex{3}\)
Determine if any of the following circles are congruent.
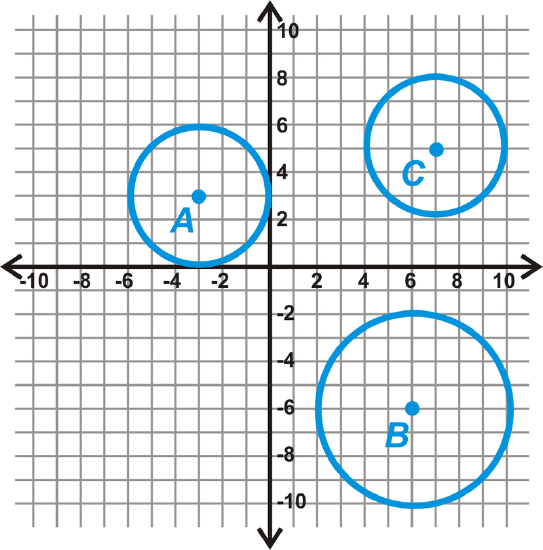
Solution
From each center, count the units to the outer rim of the circle. It is easiest to count vertically or horizontally. Doing this, we have:
\(\begin{aligned} \text{Radius of } \bigodot A&=3\text{ unit } \\ \text{Radius of } \bigodot B&=4\text{ unit }\\ \text{Radius of } \bigodot C&=3\text{ unit }\end{aligned} \)
From these measurements, we see that \(\bigodot A\cong \bigodot C\).
Notice the circles are congruent. The lengths of the radii are equal.
Example \(\PageIndex{4}\)
Is it possible to have a line that intersects a circle three times? If so, draw one. If not, explain.
Solution
It is not possible. By definition, all lines are straight. The maximum number of times a line can intersect a circle is twice.
Example \(\PageIndex{5}\)
Are all circles similar?
Solution
Yes. All circles are the same shape, but not necessarily the same size, so they are similar.
Review
Determine which term best describes each of the following parts of \(\bigodot P\).
- \(\overline{KG}\)
- \(\overleftrightarrow{FH}\)
- \(\overline{FH}\)
- \(E\)
- \(\overleftrightarrow{BK}\)
- \(\overleftrightarrow{CF}\)
- \(A\)
- \(\overline{JG}\)
- What is the longest chord in any circle?
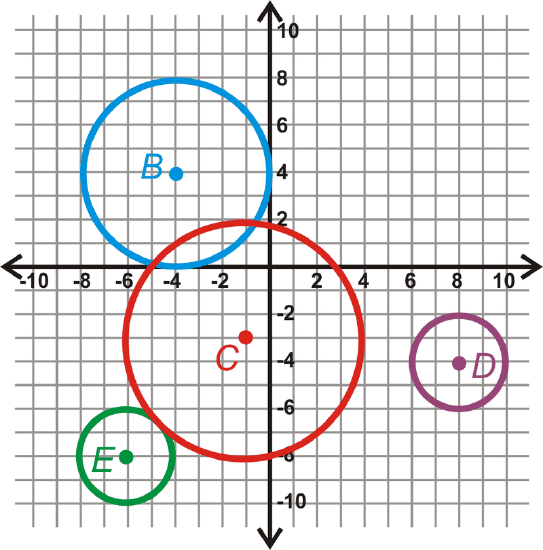
Use the graph below to answer the following questions.
- Find the radius of each circle.
- Are any circles congruent? How do you know?
- Find all the common tangents for \(\bigodot B\) and \(\bigodot C\).
- \(\bigodot C\) and \(\bigodot E\) are externally tangent. What is \(CE\)?
- Find the equation of \(\overline{CE}\).
Resources
Vocabulary
| Term | Definition |
|---|---|
| chord | A line segment whose endpoints are on a circle. |
| Circle | A circle is the set of all points at a specific distance from a given point in two dimensions. |
| concentric circles | Two or more circles that have the same center, but different radii. |
| congruent circles | Two or more circles with the same radius, but different centers. |
| Diameter | Diameter is the measure of the distance across the center of a circle. The diameter is equal to twice the measure of the radius. |
| point of tangency | The point where the tangent line touches the circle. |
| Radius | The radius of a circle is the distance from the center of the circle to the edge of the circle. |
| Circumference | The circumference of a circle is the measure of the distance around the outside edge of a circle. |
| Secant | The secant of an angle in a right triangle is the value found by dividing length of the hypotenuse by the length of the side adjacent the given angle. The secant ratio is the reciprocal of the cosine ratio. |
| Tangent | The tangent of an angle in a right triangle is a value found by dividing the length of the side opposite the given angle by the length of the side adjacent to the given angle. |
| Tangent Circles | Tangent Circles are two or more circles that intersect at one point. |
Additional Resources
Interactive Element
Video: Introduction to Circles
Activities: Parts of Circles Discussion Questions
Study Aids: Properties of a Circle Study Guide
Practice: Identify Circle Components
Real World: A Roundabout Way Home

