6.7: Areas of Combined Figures Involving Semicircles
- Page ID
- 5020
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Calculate areas of irregular shapes.
Areas of Combined Figures Involving Circles

Most of the outdoor basketball court was already repainted green. The only part left to redo was the brown key. The painters need to know the total area of the space remaining in order to buy enough paint. Given the dimensions shown below, what area should the workers use to calculate their supplies?
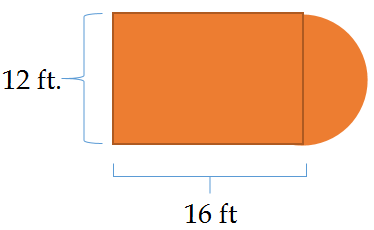
In this concept, you will learn how to find the area of composite figures containing circles.
Finding the Area of Composite Figures
The formula to find the area of a rectangle is \(A=lw\). The formula to find the area of a circle is \(A=\pi r^2\). To find the area of a composite shape, simply find the area of each individual shape and add them together. The order in which you calculate the areas does not matter, and the commutative property states that it does not matter which order you add them in.
Let’s look at an example.
Find the area of the figure below.
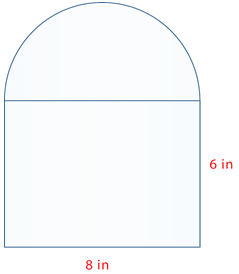
First, find the area of the rectangle.
\(\begin{aligned} A&=lw \\ A&=6(8) \\ A&=48\end{aligned}\)
The area of the rectangle is 48 square inches.
Next, recognize that you have been given a diameter and need to divide that by 2 to get the radius.
\(\begin{aligned} A&=\pi r^2 \\ A&=3.14(4)^{2} \\ A&=3.14(16) \\ A&=50.24\text{ sq. in. } \end{aligned}\)
The area of a full circle is 50.24 square inches.
Then, find the area of one half the circle, a semi-circle, by dividing your final answer by 2.
\(A=25.12\)
The area of the semi-circle is 25.12 square inches.
Finally, add the two areas together.
\(\begin{aligned} A&=A_{r}+A_{sc} \\ A&=48+25.12 \\ A&=73.12\text{ sq. in. } \end{aligned}\)
The answer is the composite figure has an area of 73.12 square inches.
Example \(\PageIndex{1}\)
Earlier, you were given a problem about the outdoor basketball court, which needs some paint.
The workers had the following court dimensions and need to know the total area to figure out their supplies.
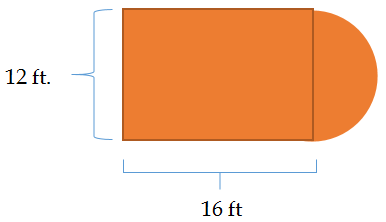
Solution
First, find the area of the rectangle.
\(\begin{aligned}A&=lw \\ A&=16(12) \\ A&=192\end{aligned}\)
The area of the rectangle is 192 square feet.
Next, recognize that you have been given a diameter and need to divide that by 2 to get the radius. The problem states that the diameter of the circle is the same as the width of the rectangle, 3 feet.
\(\begin{aligned} A&=\pi r^2 \\ A&=3.14(6)^{2} \\ A&=3.14(36) \\ A&=113.04\end{aligned}\)
The area for a full circle is approximately 113 square feet.
Then, remember that you have a semi-circle and divide this area by 2.
\(A_{sc}=56.5\)
The area of the semi-circle is 56.5 square feet.
Add the two areas together.
\(\begin{aligned} A&=A_{r}+A_{sc} \\ A&=192+56.5 \\ A&=248.5\text{ sq. ft. }\end{aligned}\)
The answer is the composite figure has an are\(A=248.5\text{ square feet }\). The workers will need to by enough paint to cover 248.5 sq. ft.
Example \(\PageIndex{2}\)
The figure below is two semi-circles with a square in the middle. The square has a side length of 6 inches.
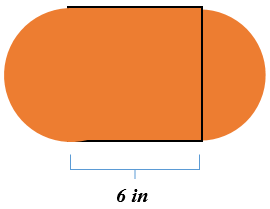
Solution
Next, determine the area of the square.
\(\begin{aligned} A&=s^2 \\ A&=6^2 \\ A&=36\end{aligned}\)
The area of the square is 36 square inches.
Then, recognize that since the square has four equal sides, the diameter of the circle is also 6 inches.
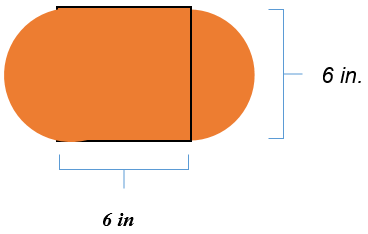
The formula for the area of one semi-circle is the formula for the area of a circle divided by 2.
\(A_{sc}=\dfrac{\pi r^2}{2}\)
Since there are two semi-circles the same size, you may simply add them together to end up with the area for the complete circle.
Remember that you have been given a diameter, not a radius, so divide the diameter by 2.
Then, use the formula for the area of a circle.
\(\begin{aligned} A&=\pi r^2 \\ A&=3.14(3)^{2} \\ A&=3.14(9) \\ A&=28.26\end{aligned}\)
The area of the two semi-circles that form one full circle is 28.26 square inches.
Finally, add the two areas together.
\(\begin{aligned} A&=A_{r}+A_{sc} \\ A&=36+28.26 \\ A&=64.26\end{aligned}\)
The answer is the composite figure has an are\(A=64.26\text{ square inches }\)
Example \(\PageIndex{3}\)
Find the composite area of a rectangle with a length of 5 feet and a width of 3 feet connected to a semi-circle with the same diameter as the width.
Solution
First, find the area of the rectangle.
\(\begin{aligned} A&=lw \\ A&=5(3) \\ A&=15\end{aligned}\)
The area of the rectangle is 15 square feet.
Next, recognize that you have been given a diameter and need to divide that by 2 to get the radius. The problem states that the diameter of the circle is the same as the width of the rectangle, 3 feet.
\(\begin{aligned} A&=\pi r^2 \\ A&=3.14(1.5)^{2} \\ A&=3.14(2.25) \\ A&=7.065\end{aligned}\)
The area for a full circle is 7.065 square feet.
Then, remember that you have a semi-circle and divide this area by 2.
\(A_{sc}=3.53\)
The area of the semi-circle is 3.53 square feet.
Add the two areas together.
\(\begin{aligned} A&=A_{r}+A_{sc} \\ A&=15+3.53 \\ A&=18.53\text{ sq. ft. }.\end{aligned}\)
The answer is the composite figure has an are\(A=18.53 \text{ square feet }\).
Example \(\PageIndex{4}\)
Find the composite area of a square with a side length of 4 mm and a semi-circle with a diameter of the same side length as the square.
Solution
First, find the area of the square.
\(\begin{aligned} A&=s^2 \\ A&=4^2 \\ A&=16 \end{aligned}\)
The area of the square is 16 square millimeters.
Next, recognize that you have been given a diameter and need to divide that by 2 to get the radius. The problem states that the diameter of the circle is the same as the side length of the square, 4 mm.
\(\begin{aligned} A&=\pi r^2 \\ A&=3.14(2)^{2} \\ A&=3.14(4) \\ A&=12.56\end{aligned}\)
The area for a full circle is 12.56 square millimeters.
Then, remember that you have a semi-circle and divide this area by 2.
\(A_{sc}=6.28\)
The area of the semi-circle is 6.28 square millimeters.
Add the two areas together.
\(\begin{aligned} A&=AS+A_{sc} \\ A&=16+6.28 \\ A&=22.28\text{ sq. mm. }\end{aligned}\)
The answer is the composite figure has an are\(A=22.28\text{ sq. mm. }\)
Example \(\PageIndex{5}\)
Find the area of a figure that is made up of a square and a semi-circle. The square has a side length of 8 inches. The circle’s diameter is the same as the side length of the square.
Solution
First, find the area of the square.
\(\begin{aligned} A&=s^2 \\ A&=8^2 \\ A&=64\end{aligned} \)
The area of the square is 64 square inches.
Next, recognize that you have been given a diameter and need to divide that by 2 to get the radius. The problem states that the diameter of the circle is the same as the side length of the square, 8 inches.
\(\begin{aligned} A&=\pi r^2 \\ A&=3.14(4)^{2} \\ A&=3.14(16) \\ A&=50.24 \end{aligned}\)
The area for a full circle is 50.24 square inches.
Then, remember that you have a semi-circle and divide this area by 2.
\(A_{sc}=25.12\)
The area of the semi-circle is 25.12 square inches.
Add the two areas together.
\(\begin{aligned} A&=A_{r}+A_{sc} \\ A&=64+25.12 \\ A&=79.12\text{ square inches } \end{aligned}\)
The answer is the composite figure has an are\(A=79.12\text{ sq. in. }\)
Review
Find the area of each combined figure.
- A square and a semi-circle. The square has a side length of 11 mm. The diameter of the circle matches the square’s side.
- A square and a semi-circle. The square has a side length of 8.5 inches. The diameter of the circle matches the square’s side.
- A square and a semi-circle. The square has a side length of 7.25 inches. The diameter of the circle matches the square’s side.
- A square and a semi-circle. The square has a side length of 13 feet. The diameter of the circle matches the square’s side.
- A square and a semi-circle. The square has a side length of 15.5 feet. The diameter of the circle matches the square’s side.
- A rectangle and a semi-circle. The rectangle has a length of 8 feet and a width of 5 feet. The diameter of the circle matches the width.
- A rectangle and a semi-circle. The rectangle has a length of 8.5 feet and a width of 6 feet. The diameter of the circle matches the width.
- A rectangle and a semi-circle. The rectangle has a length of 9 inches and a width of 4.5 inches. The diameter of the circle matches the length.
- A rectangle and a semi-circle. The rectangle has a length of 7 feet and a width of 4 feet. The diameter of the circle matches the length.
- A rectangle and a semi-circle. The rectangle has a length of 5.5 feet and a width of 3.5 feet. The diameter of the circle matches the width.
- A triangle and a semi-circle. The triangle has a base of 5 inches and a height of 4 inches. The diameter of the circle matches the base of the triangle.
- A triangle and a semi-circle. The triangle has a base of 7 inches and a height of 6 inches. The diameter of the circle matches the base of the triangle.
- A triangle and a semi-circle. The triangle has a base of 5.5 inches and a height of 4 inches. The diameter of the circle matches the base of the triangle.
Solve each problem.
- Rob is painting large polka dots on a sheet for the backdrop of the school musical. He painted 16 polka dots, each with a radius of 3 feet. What is the total area that the polka dots cover?
- The librarian is having the library at her school carpeted. The library is a circular room with a diameter of 420 feet. How many square feet of carpet will she need to order?
Resources
Vocabulary
| Term | Definition |
|---|---|
| Area | Area is the space within the perimeter of a two-dimensional figure. |
| Circle | A circle is the set of all points at a specific distance from a given point in two dimensions. |
| Diameter | Diameter is the measure of the distance across the center of a circle. The diameter is equal to twice the measure of the radius. |
Additional Resources
Video: Area and Perimeter
Practice: Areas of Combined Figures Involving Semicircles
Real World: Shooting Circles

