Skip to main content
K12 LibreTexts

7.18: Self-Similarity and Fractals

  1. Last updated
  2. Save as PDF
  • Page ID
    5952

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    One part of an object can be enlarged or shrunk to look like the whole object.

    Self-Similarity

    When one part of an object can be enlarged (or shrunk) to look like the whole object it is self-similar.

    To explore self-similarity, we will go through some examples. Typically, each step of a process is called an iteration. The first level is called Stage 0.

    What if you were given an object, like a triangle or a snowflake, in which a part of it could be enlarged (or shrunk) to look like the whole object? What would each successive iteration of that object look like?

    Example \(\PageIndex{1}\)

    The Sierpinski triangle iterates a triangle by connecting the midpoints of the sides and shading the central triangle (Stage 1). Repeat this process for the unshaded triangles in Stage 1 to get Stage 2.

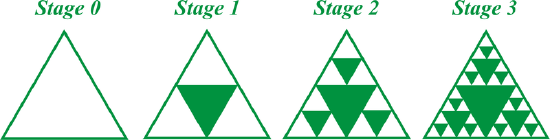
    f-d_544981997fcbf4120b476154db63cfe52721cd9935235ca1ba3fa2b2+IMAGE_TINY+IMAGE_TINY.png
    Figure \(\PageIndex{1}\)

    Example \(\PageIndex{2}\)

    Determine the number of shaded and unshaded triangles in each stage of the Sierpinkski triangle. Determine if there is a pattern.

    Stage 0 Stage 1 Stage 2 Stage 3
    Unshaded 1 3 9 27
    Shaded 0 1 4 13

    Solution

    The number of unshaded triangles seems to be powers of \(3:\: 3^{0},\: 3^{1},\: 3^{2},\: 3^{3},\: ….\) The number of shaded triangles is the sum the number of shaded and unshaded triangles from the previous stage. For Example, the number of shaded triangles in Stage 4 would equal \(27 + 13 = 40\).

    Example \(\PageIndex{3}\)

    Like the Sierpinski triangle, a fractal is another self-similar object that is repeated at smaller scales. Below are the first three stages of the Koch snowflake.

    f-d_e89ba495df3dfe3277948ddb0e0a92dfb462edd5bb6faf8ddbec1585+IMAGE_TINY+IMAGE_TINY.png
    Figure \(\PageIndex{2}\)

    Example \(\PageIndex{4}\)

    Determine the number of edges and the perimeter of each snowflake shown in Example 3. Assume that the length of one side of the original (stage 0) equilateral triangle is 1.

    Stage 0 Stage 1 Stage 2
    Number of Edges 3 12 48
    Edge Length 1 \(\dfrac{1}{3}\) \(\dfrac{1}{9}\)
    Perimeter 3 4 \(\dfrac{48}{9}=\dfrac{15}{3}\)

    Example \(\PageIndex{5}\)

    The Cantor set is another example of a fractal. It consists of dividing a segment into thirds and then erasing the middle third.

    f-d_9fb958f0528d884b2dc31f4e89a5bb7a5a639abb9e59e024f801df9b+IMAGE_TINY+IMAGE_TINY.png
    Figure \(\PageIndex{3}\)

    Review

    1. Draw Stage 4 of the Cantor set.
    2. Use the Cantor Set to fill in the table below.
    Number of Segments Length of each Segment Total Length of the Segments
    Stage 0 1 1 1
    Stage 1 2 \(\dfrac{1}{3}\) \(\dfrac{2}{3}\)
    Stage 2 4 \(\dfrac{1}{9}\) \(\dfrac{4}{9}\)
    Stage 3
    Stage 4
    Stage 5
    1. How many segments are in Stage \(n\)?
    2. Draw Stage 3 of the Koch snowflake.
    3. A variation on the Sierpinski triangle is the Sierpinski carpet, which splits a square into 9 equal squares, coloring the middle one only. Then, split the uncolored squares to get the next stage. Draw the first 3 stages of this fractal.
    4. How many colored vs. uncolored square are in each stage?
    5. Fractals are very common in nature. For example, a fern leaf is a fractal. As the leaves get closer to the end, they get smaller and smaller. Find three other examples of fractals in nature.
    f-d_a3e71883dff558cf8bf97594ca7687a346d82ab1c6ecb79d6b66e742+IMAGE_TINY+IMAGE_TINY.png
    Figure \(\PageIndex{4}\)

    Review (Answers)

    To see the Review answers, open this PDF file and look for section 7.13.

    Vocabulary

    Term Definition
    self-similar When one part of an object can be enlarged (or shrunk) to look like the whole object.
    Iteration An iteration is a single step within a process.
    midpoint The midpoint of a line segment is the point on the line segment that splits the segment into two congruent parts.

    Additional Resources

    Interactive Element

    Video: Self-Similarity Examples - Basic

    Activities: Self-Similarity Discussion Questions

    Study Aids: Self-Similarity Study Guide

    Practice: Self-Similarity and Fractals

    Real World: Fractals Everywhere

    This page titled 7.18: Self-Similarity and Fractals is shared under a CK-12 license and was authored, remixed, and/or curated by CK-12 Foundation via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.

    CK-12 Foundation
    LICENSED UNDER
    CK-12 Foundation is licensed under CK-12 Curriculum Materials License
    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Author
      CK12
      License
      CK-12
      OER program or Publisher
      CK-12
      Show TOC
      no
    2. Tags
      1. source@https://www.ck12.org/c/geometry