2.4: Rational Expressions

A rational expression is a ratio, just like a fraction. However, instead of a ratio between numbers, a rational expression is a ratio between two expressions.

One driving question to ask is: Are the rules for simplifying and operating on rational expressions the same as the rules for simplifying and operating on fractions?

Working with Rational Expressions

When simplifying or operating on rational expressions, it is vital that each polynomial be fully factored. Once all expressions are factored, identical factors in the numerator and denominator may be canceled or removed. The reason they can be removed is that any expression divided by itself is equal to 1. An identical expression in the numerator and denominator is just an expression being divided by itself, and so equals 1.

Adding and Subtracting Rational Expressions

To add or subtract rational expressions, it is essential to first find a common denominator. While any common denominator will work, using the least common denominator is a means of keeping the number of additional factors under control. Look at each rational expression you are working with and identify your desired common denominator. Multiply each expression by an appropriate form of 1, such as \(\frac{x-2}{x-2}\), and then you should have your common denominator. In addition and subtraction problems, the numerator must be multiplied, combined, and re-factored to be considered simplified.

Multiplying and Dividing Rational Expressions

To multiply rational expressions, you should write the product of all the numerator factors over the product of all the denominator factors and then cancel, or remove, identical factors.To divide rational expressions, you should rewrite the division problem as a multiplication problem. Multiply the first rational expression by the reciprocal of the second rational expression. Follow the steps above for multiplying. In both multiplication and division problems answers are most commonly left entirely factored to demonstrate everything has been reduced appropriately.

Examples

Example 1

Earlier, you were asked if the rules for simplifying and operating on rational expressions are the same as the rules for simplifying and operating on fractions. Rational expressions are an extension of fractions and the operations of simplifying, adding, subtracting, multiplying and dividing work in exactly the same way.

Example 2

Subtract the following rational expressions.

\(\frac{x-2}{x+3}-\frac{x^{3}-3 x^{2}+8 x-24}{2(x+2)\left(x^{2}-9\right)}\)

Being able to factor effectively is of paramount importance.

\(=\frac{x-2}{x+3}-\frac{x^{3}-3 x^{2}+8 x-24}{2(x+2)\left(x^{2}-9\right)}\)
\(=\frac{(x-2)}{(x+3)}-\frac{x^{2}(x-3)+8(x-3)}{2(x+2)\left(x^{2}-9\right)}\)
\(=\frac{(x-2)}{(x+3)}-\frac{(x-3)\left(x^{2}+8\right)}{2(x+2)(x+3)(x-3)}\)

Before subtracting, simplify where possible so you don’t contribute to unnecessarily complicated denominators.

\(=\frac{(x-2)}{(x+3)}-\frac{x^{2}+8}{2(x+2)(x+3)}\)

The left expression lacks \(2(x+2)\), so multiply both its numerator and denominator by \(2(x+2)\)

\(=\frac{2(x+2)(x-2)}{2(x+2)(x+3)}-\frac{\left(x^{2}+8\right)}{2(x+2)(x+3)}\)
\(=\frac{2\left(x^{2}-4\right)-x^{2}-8}{2(x+2)(x+3)}\)
\(=\frac{x^{2}-16}{2(x+2)(x+3)}\)

Example 3

Simplify the following rational expression.

\(\frac{x^{2}+7 x+12}{x^{2}+4 x+3} \cdot \frac{x^{2}+9 x+8}{2 x^{2}-128} \div \frac{x+4}{x-8} \cdot \frac{14}{1}\)

First factor everything. Second, turn division into multiplication (only one term). Third, cancel appropriately which will leave the answer.

\(=\frac{(x+3)(x+4)}{(x+3)(x+1)} \cdot \frac{(x+8)(x+1)}{2(x+8)(x-8)} \cdot \frac{(x-8)}{(x+4)} \cdot \frac{14}{1}\)
\(=\frac{(x+3)(x+4)}{(x+3)(x+1)} \cdot \frac{(x+8)(x+1)}{2(x+8)(x-8)} \cdot \frac{(x-8)}{(x+4)} \cdot \frac{14}{1}\)
\(=\frac{14}{2}\)
\(=7\)

In this example, the strike through is shown. You should use this technique to match up factors in the numerator and the denominator when simplifying.

Example 4

Combine the following rational expressions.

\(\frac{1}{x^{2}+5 x+6}-\frac{1}{x^{2}-4}+\frac{(x-7)(x+5)+5}{(x+2)(x-2)(x+3)(x-4)}\)

First factor everything and decide on a common denominator. While the numerators do not really need to be factored, it is sometimes helpful in simplifying individual expressions before combining them. Note that the numerator of the expression on the right hand seems factored but it really is not. Since the 5 is not connected to the rest of the numerator through multiplication, that part of the expression needs to be multiplied out and like terms need to be combined.

\(=\frac{1}{(x+2)(x+3)}-\frac{1}{(x+2)(x-2)}+\frac{x^{2}-2 x-35+5}{(x+2)(x-2)(x+3)(x-4)}\)
\(=\frac{1}{(x+2)(x+3)}-\frac{1}{(x+2)(x-2)}+\frac{x^{2}-2 x-30}{(x+2)(x-2)(x+3)(x-4)}\)

Note that the right expression has 4 factors in the denominator while each of the left expressions have two that match and two that are missing from those four factors. This tells you what you need to multiply each expression by in order to have the denominators match up.

\(=\frac{(x-2)(x-4)}{(x+2)(x-2)(x+3)(x-4)}-\frac{(x+3)(x-4)}{(x+2)(x-2)(x+3)(x-4)}+\frac{x^{2}-2 x-30}{(x+2)(x-2)(x+3)(x-4)}\)

Now since the rational expressions have a common denominator, the numerators may be multiplied out and combined. Sometimes instead of rewriting an expression repeatedly in mathematics you can use an abbreviation. In this case, you can replace the denominator with the letter \(D\) and then replace it at the end.

\(=\frac{(x-2)(x-4)-(x+3)(x-4)+x^{2}-2 x-30}{D}\)
\(=\frac{x^{2}-6 x+8-\left[x^{2}-x-12\right]+x^{2}-2 x-30}{D}\)

Notice how it is extremely important to use brackets to indicate that the subtraction applies to all the terms of the middle expression not just \(x^{2}\). This is one of the most common mistakes.

\(=\frac{x^{2}-6 x+8-x^{2}+x+12+x^{2}-2 x-30}{D}\)
\(=\frac{x^{2}-7 x-10}{D}\)

After the numerator has been entirely simplified try to factor the remaining expression and see if anything cancels with the denominator which you now need to replace.

\(=\frac{(x+2)(x-5)}{(x+2)(x-2)(x+3)(x-4)}\)
\(=\frac{(x-5)}{(x-2)(x+3)(x-4)}\)

Example 5

Simplify the following expression.

\(\frac{\frac{1}{x+1}-\frac{1}{x+2}}{\frac{1}{x-2}-\frac{1}{x+1}}\)

The expression itself does not look like a rational expression, but it can be rewritten so it is more recognizable. Also, working with fractions within fractions is an important skill.

\(=\left(\frac{1}{x+1}-\frac{1}{x+2}\right) \div\left(\frac{1}{x-2}-\frac{1}{x+1}\right)\)
\(=\left[\frac{(x+2)}{(x+1)(x+2)}-\frac{(x+1)}{(x+1)(x+2)}\right] \div\left[\frac{(x+1)}{(x+1)(x-2)}-\frac{(x-2)}{(x+1)(x-2)}\right]\)
\(=\left[\frac{1}{(x+1)(x+2)}\right] \div\left[\frac{3}{(x+1)(x-2)}\right]\)
\(=\frac{1}{(x+1)(x+2)} \cdot \frac{(x+1)(x-2)}{3}\)
\(=\frac{(x-2)}{3(x+2)}\)

Bonus Example

Simplify the following expression which has an infinite number of fractions nested within other fractions.

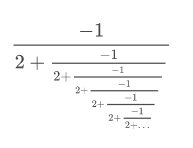
It would be an exercise in futility to attempt to try to compute this expression directly. Instead, notice that the repeating nature of the expression lends itself to an extremely nice substitution.

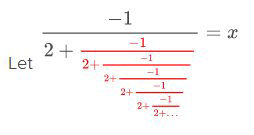
Notice that the red portion of the fraction is exactly the same as the rest of the fraction and so \(x\) may be substituted there and solved.

\(\begin{aligned} \frac{-1}{2+x} &=x \\-1 &=x(2+x) \\-1 &=x^{2}+2 x \\ 0 &=x^{2}+2 x+1 \\ 0 &=(x+1)^{2} \\ x &=-1 \end{aligned}\)

The reason why this expression is included in this concept is because it highlights one problem solving aspect of simplifying expressions that distinguishes PreCalculus from Algebra 1 and Algebra 2.

Review

Perform the indicated operation and simplify as much as possible.

1. \(\frac{x^{2}+5 x+4}{x^{2}+4 x+3} \cdot \frac{5 x^{2}+15 x}{x+4}\)

2. \(\frac{x^{2}-4}{x^{2}+4 x+4} \cdot \frac{7}{x-2}\)

3. \(\frac{4 x^{2}-12 x}{5 x+10} \cdot \frac{x+2}{x} \div \frac{x-3}{1}\)

4. \(\frac{4 x^{3}-4 x}{x} \div \frac{2 x-2}{x-4}\)

5. \(\frac{2 x^{3}+8 x}{x+1} \div \frac{x}{2 x^{2}-2}\)

6. \(\frac{3 x-1}{x^{2}+2 x-15}-\frac{2}{x+5}\)

7. \(\frac{x^{2}-8 x+7}{x^{2}-4 x-21} \cdot \frac{x^{2}-9}{1-x^{2}}\)

8. \(\frac{2}{x+7}+\frac{1}{x-7}\)

9. \(\frac{6}{x-7}-\frac{6}{x+7}\)

10. \(\frac{3 x+35}{x^{2}-25}+\frac{2}{x+5}\)

11. \(\frac{2 x+20}{x^{2}-4 x-12}+\frac{2}{x+2}\)

12. \(\frac{2}{x+6}-\frac{x-9}{x^{2}-3 x-18}\)

13. \(-\frac{5 x+30}{x^{2}+11 x+30}+\frac{2}{x+5}\)

14. \(\frac{x+3}{x+2}+\frac{x^{3}+4 x^{2}+5 x+20}{2 x^{4}+2 x^{2}-40}\)

15. \(\frac{-4}{2+\frac{-4}{2+\frac{-4}{2+\frac{-4}{2+\frac{-4}{2+\frac{-4}{2+\cdots}}}}}}\)