2.5: Polynomial Long Division and Synthetic Division

While you may be experienced in factoring, there will always be polynomials that do not readily factor using basic or advanced techniques. How can you identify the roots of these polynomials?

Rational Roots and Dividing Polynomials

There are numerous theorems that point out relationships between polynomials and their factors. For example there is a theorem that a polynomial of degree \(n\) must have exactly \(n\) solutions/factors that may or may not be real numbers. The Rational Root Theorem and the Remainder Theorem are two theorems that are particularly useful starting places when manipulating polynomials.

The Rational Root Theorem

The Rational Root Theorem states that in a polynomial, every rational solution can be written as a reduced fraction \(\left(x=\frac{p}{q}\right),\) where \(p\) is an integer factor of the constant term and \(q\) is an integer factor of the leading coefficient.

Let's identify all the possible rational solutions of the following polynomial using the Rational Root Theorem.

\(12 x^{18}-91 x^{17}+x^{16}+\cdots+2 x^{2}-14 x+5=0\)

The integer factors of 5 are 1,5 . The integer factors of 12 are 1,2,3,4,6 and \(12 .\) since pairs of factors could both be negative, remember to include \(\pm\).

\(\pm \frac{p}{q}=\frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{6}, \frac{1}{12}, \frac{5}{1}, \frac{5}{2}, \frac{5}{3}, \frac{5}{4}, \frac{5}{6}, \frac{5}{12}\)

The possible solutions can be found from these 24 possible rational answers. If this question required you to find a solution, then the Rational Root Theorem would give you a great starting place. Once you have one root, you can use either polynomial long division or synthetic to divide the factor out and to keep reducing the expression. We will use the Rational Root Theorem in Example 3.

Polynomial Long Division and the Remainder Theorem

Polynomial long division is identical to regular long division except the dividend and divisor are both polynomials instead of numbers.

The Remainder Theorem states that the remainder of a polynomial \(f(x)\) divided by a linear divisor \((x-a)\) is equal to \(f(a)\). The Remainder Theorem is only useful after you have performed polynomial long division because you are usually never given the divisor and the remainder to start. The main purpose of the Remainder Theorem in this setting is a means of double checking your application of polynomial long division.

Let's put this knowledge to use and use polynomial long division to divide:

\(\frac{x^{3}+2 x^{2}-5 x+7}{x-3}\)

First note that it is clear that 3 is not a root of the polynomial because of the Rational Root Theorem and so there will definitely be a remainder. Start a polynomial long division question by writing the problem like a long division problem with regular numbers:

\(- x - 3 \longdiv { x ^ { 3 } + 2 x ^ { 2 } - 5 x + 7 }\)

First note that it is clear that 3 is not a root of the polynomial because of the Rational Root Theorem and so there will definitely be a remainder. Start a polynomial long division question by writing the problem like a long division problem with regular numbers:

\(- x - 3 \longdiv { x ^ { 3 } + 2 x ^ { 2 } - 5 x + 7 }\)

Just like with regular numbers ask yourself "how many times does \(x\) go into \(x^{3}\) ?" which in this case is \(x^{2}\).

\(\frac{x^{2}}{x-3) x^{3}+2 x^{2}-5 x+7}\)

Now multiply the \(x^{2}\) by \(x-3\) and copy below. Remember to subtract the entire quantity.

\begin{tabular}{c}
\(x^{2}\) \\
\hline\(x-3) x^{3}+2 x^{2}-5 x+7\) \\
\(-\left(x^{3}-3 x^{2}\right)\)
\end{tabular}

Combine the rows, bring down the next number and repeat.

\(\frac{x^{2}+5 x+10}{3) x^{3}+2 x^{2}-5 x+7}\)
\(\frac{-\left(x^{3}-3 x^{2}\right)}{5 x^{2}-5 x}\)
\(\frac{-\left(5 x^{2}-15 x\right)}{10 x+7}\)
\(\frac{-(10 x-30)}{37}\)

The number 37 is the remainder. There are two things to think about at this point. First, interpret in an equation:

\(\frac{x^{3}+2 x^{2}-5 x+7}{x-3}=\left(x^{2}+5 x+10\right)+\frac{37}{x-3}\)

Second, check your result with the Remainder Theorem which states that the original function evaluated at 3 must be 37 . Notice the notation indicating to substitute 3 in for \(x\).

\(\left.\left(x^{3}+2 x^{2}-5 x+7\right)\right|_{x=3}=3^{3}+2 \cdot 3^{2}-5 \cdot 3+7=27+18-15+7=37\)

Synthetic Division

Synthetic division is an abbreviated version of polynomial long division where only the coefficients are used. Synthetic division is mostly used when the leading coefficients of the numerator and denominator are equal to 1 and the divisor is a first degree binomial. Let's use synthetic division to divide the same expression that we divided above with polynomial long division:

\(\frac{x^{3}+2 x^{2}-5 x+7}{x-3}\)

Instead of continually writing and rewriting the \(x\) symbols, synthetic division relies on an ordered spacing.

\(\pm 3 \mid \begin{array}{llll}1 & 2 & -5 & 7\end{array}\)

Notice how only the coefficients for the denominator are used and the divisor includes a positive three rather than a negative three. The first coefficient is brought down and then multiplied by the three to produce the value which goes beneath the 2.

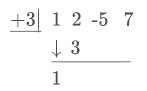
Next the new column is added. \(2+3=5,\) which goes beneath the \(2^{n d}\) column. Now, multiply \(5 \cdot+3=15\), which goes underneath the -5 in the \(3^{r d}\) column. And the process repeats...

The last number, 37, is the remainder. When writing out the resulting expression, you will put this remainder over the divisor. The three other numbers represent the quadratic that is identical to the solution to the result from dividing the expression using polynomial long division. Note that when writing out the expression, you decrease the exponent of the leading coefficient of the original by 1.

\(\left(1 x^{2}+5 x+10\right)+\frac{37}{x-3}\)

Examples

Example 1

Earlier, you were asked about identifying roots of polynomials that do not readily factor using the techniques you have learned so far. Identifying roots of polynomials by hand can be tricky business. The best way to identify roots is to use the rational root theorem to quickly identify likely candidates for solutions and then use synthetic or polynomial long division to quickly and effectively test them to see if their remainders are truly zero.

Example 2

Divide the following polynomials.

\(\frac{x^{3}+2 x^{2}-4 x+8}{x-2}\)

Since the leading coefficients of the numerator and denominator are both 1 and the denominator is a binomial, synthetic division is a good method to use here.

\(\frac{x^{3}+2 x^{2}-4 x+8}{x-2}=x^{2}+4 x+4+\frac{16}{x-2}\)

Example 3

Completely factor the following polynomial.

\(x^{4}+6 x^{3}+3 x^{2}-26 x-24\)

Notice that possible roots are ±1,2,3,4,6,8,24 . Of these 14 possibilities, four will yield a remainder of zero. When you find one, use long division or synthetic division to factor out the root that you found. Then find another zero and repeat the process.

\(x^{4}+6 x^{3}+3 x^{2}-26 x-24\)
\(=(x+1)\left(x^{3}+5 x^{2}-2 x-4\right)\)
\(=(x+1)(x-2)\left(x^{2}+7 x+12\right)\)
\(=(x+1)(x-2)(x+3)(x+4)\)

The first zero found was -1. It was divided out of the original expression to find the remaining non-factored portion of the expression. The second zero found was 2 from the remaining piece and was divided out. Once you get down to a quadratic expression, you can use the other factoring techniques you know to factor the rest of the expression.

Example 4

Divide the following polynomials.

\(\frac{3 x^{5}-2 x^{2}+10 x-5}{x-1}\)

Since the first coefficient of the numerator is not 1, polynomial long division is a good method to use here.

\(\frac{3 x^{5}-2 x^{2}+10 x-5}{x-1}=3 x^{4}+3 x^{3}+3 x^{2}+x+11+\frac{6}{x-1}\)

Review

Identify all possible rational solutions of the following polynomials using the Rational Root Theorem.

1. \(15 x^{14}-12 x^{13}+x^{12}+\cdots+2 x^{2}-5 x+5=0\)

2. \(18 x^{11}+42 x^{10}+x^{9}+\cdots+x^{2}-3 x+7=0\)

3. \(12 x^{16}+11 x^{15}+3 x^{14}+\cdots+6 x^{2}-2 x+11=0\)

4. \(14 x^{7}-7 x^{6}+x^{5}+\cdots+x^{2}+6 x+3=0\)

5. \(9 x^{9}-10 x^{8}+3 x^{7}+\cdots+4 x^{2}-2 x+2=0\)

Completely factor the following polynomials.

6. \(2 x^{4}-x^{3}-21 x^{2}-26 x-8\)

7. \(x^{4}+7 x^{3}+5 x^{2}-31 x-30\)

8. \(x^{4}+3 x^{3}-8 x^{2}-12 x+16\)

9. \(4 x^{4}+19 x^{3}-48 x^{2}-117 x-54\)

10. \(2 x^{4}+17 x^{3}-8 x^{2}-173 x+210\)

Divide the following polynomials.

11. \(\frac{x^{4}+7 x^{3}+5 x^{2}-31 x-30}{x+4}\)

12. \(\frac{x^{4}+7 x^{3}+5 x^{2}-31 x-30}{x+2}\)

13. \(\frac{x^{4}+3 x^{3}-8 x^{2}-12 x+16}{x+3}\)

14. \(\frac{2 x^{4}-x^{3}-21 x^{2}-26 x-8}{x^{3}-x^{2}-10 x-8}\)

15. \(\frac{x^{4}+8 x^{3}+3 x^{2}-32 x-28}{x^{3}+10 x^{2}+23 x+14}\)