2.7 Holes in Rational Functions
- Page ID
- 13712
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In a function like \(f(x)=\frac{(3 x+1)(x-1)}{(x-1)},\) you should note that the factor \((x-1)\) clearly cancels leaving only \(3 x-1\). This appears to be a regular line. What happens to this line at \(x=1\) ?
Holes and Rational Functions
A hole on a graph looks like a hollow circle. It represents the fact that the function approaches the point, but is not actually defined on that precise \(x\) value.
Take a look at the graph of the following equation:
\(f(x)=(2 x+2) \cdot \frac{\left(x+\frac{1}{2}\right)}{\left(x+\frac{1}{2}\right)}\)
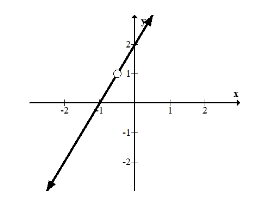
The reason why this function is not defined at \(-\frac{1}{2}\) is because \(-\frac{1}{2}\) is not in the domain of the function. As you can see, \(f\left(-\frac{1}{2}\right)\) is undefined because it makes the denominator of the rational part of the function zero which makes the whole function undefined. Also notice that once the factors are canceled/removed then you are left with a normal function which in this case is \(2 x+2\). The hole in this situation is at \(\left(-\frac{1}{2}, 1\right)\) because after removing the factors that cancel, \(f\left(-\frac{1}{2}\right)=1\)
This is the essence of dealing with holes in rational functions. You should cancel what you can and graph the function like normal making sure to note what \(x\) values make the function undefined. Once the function is graphed without holes go back and insert the hollow circles indicating what \(x\) values are removed from the domain. This is why holes are called removable discontinuities.
Watch the first part of this video and focus on holes in rational equations.
Examples
Earlier, you were asked what happens to the equation \(f(x)=\frac{(3 x+1)(x-1)}{(x-1)}\) at \(x=1\). since this function that is not defined at \(x=1\) there is a removable discontinuity that is represented as a hollow circle on the graph. Otherwise the function behaves precisely as \(3 x+1\).
Graph the following rational function and identify any removable discontinuities.
\(f(x)=\frac{-x^{3}+3 x^{2}+2 x-4}{x-1}\)
This function requires some algebra to change it so that the removable factors become obvious. You should suspect that \((x-1)\) is a factor of the numerator and try polynomial or synthetic division to factor. When you do, the function becomes:
\(f(x)=\frac{\left(-x^{2}+2 x+4\right)(x-1)}{(x-1)}\)
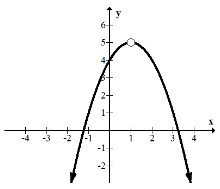
The removable discontinuity occurs at (1, 5).
Graph the following rational function and identify any removable discontinuities.
\(f(x)=\frac{x^{6}-6 x^{5}+5 x^{4}+27 x^{3}-48 x^{2}-9 x+54}{x^{3}-7 x-6}\)
This is probably one of the most challenging rational expressions with only holes that people ever try to graph by hand. There are multiple ways to start, but a good habit to get into is to factor everything you possibly can initially. The denominator seems less complicated with possible factors \((x \pm 1),(x \pm 2),(x \pm 3),(x \pm 6) .\) Using polynomial division, you will find the denominator becomes:
\(f(x)=\frac{x^{6}-6 x^{5}+5 x^{4}+27 x^{3}-48 x^{2}-9 x+54}{(x+1)(x+2)(x-3)}\)
The factors of the denominator are strong hints as to the factors of the numerator so use polynomial division and try each. When you fully factor the numerator you will have:
\(f(x)=\frac{\left(x^{3}-6 x^{2}+12 x-9\right)(x+1)(x+2)(x-3)}{(x+1)(x+2)(x-3)}\)
Note the factors that cancel \((x=-1,-2,3)\) and then work with the cubic function that remains.
\(f(x)=x^{3}-6 x^{2}+12 x-9\)
At this point it is probably reasonable to make a table and plot points to get a sense of where this cubic function lives. You also could notice that the coefficients are almost of the pattern 1 3 3 1 which is the binomial expansion. By separating the -9 into -8 -1 you can factor the first four terms.
\(f(x)=x^{3}-6 x^{2}+12 x-8-1=(x-2)^{3}-1\)
This is a cubic function that has been shifted right by two units and down one unit.
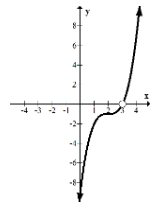
Note that there are two holes that do not fit in the graph window. When this happens you still need to note where they would appear given a properly sized window. To do this, substitute the invalid \(x\) values: \(x=-1,-2,3\) into the factored cubic that remained after canceling.
f(x)=(x-2)^{3}-1
Holes: (3, 0); (-1, -28); (-2, -65)
Without graphing, identify the location of the holes of the following function.
\(f(x)=\frac{x^{3}+4 x^{2}+x-6}{x^{2}+5 x+6}\)
First factor everything. Then, identify the \(x\) values that make the denominator zero and use those values to find the exact location of the holes.
\(f(x)=\frac{(x+2)(x+3)(x-1)}{(x+3)(x+2)}\)
Holes: (-3, -4); (-2, -3)
What is a possible equation for the following rational function?
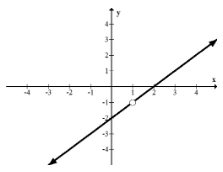
The function seems to be a line with a removable discontinuity at \((1,-1) .\) The line is has slope 1 and \(y\) -intercept of -2 and so has the equation:
\(f(x)=x-2\)
The removable discontinuity must not allow the \(x\) to be 1 which implies that it is of the form \(\frac{x-1}{x-1}\). Therefore, the function is:
\(f(x)=\frac{(x-2)(x-1)}{x-1}\)
Review
1. How do you find the holes of a rational function?
2. What’s the difference between a hole and a removable discontinuity?
3. If you see a hollow circle on a graph, what does that mean?
Without graphing, identify the location of the holes of the following functions.
4. \(f(x)=\frac{x^{2}+3 x-4}{x-1}\)
5. \(g(x)=\frac{x^{2}+8 x+15}{x+3}\)
6. \(h(x)=\frac{x^{3}+6 x^{2}+2 x-8}{x^{2}+x-2}\)
7. \(k(x)=\frac{x^{3}+6 x^{2}+2 x-8}{x^{2}-3 x+2}\)
8. \(j(x)=\frac{x^{3}+4 x^{2}-17 x-60}{x^{2}-9}\)
9. \(f(x)=\frac{x^{3}+4 x^{2}-17 x-60}{x^{2}-5 x+4}\)
10. \(g(x)=\frac{x^{3}-4 x^{2}-19 x-14}{x^{2}-8 x+7}\)
11. What is a possible equation for the following rational function?
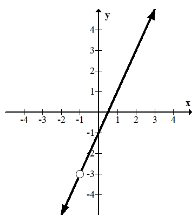
12. What is a possible equation for the following rational function?
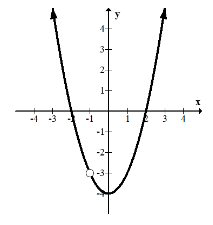
Sketch the following rational functions.
13. \(f(x)=\frac{x^{3}+4 x^{2}-17 x-60}{x^{2}-x-12}\)
14. \(g(x)=\frac{x^{3}+4 x^{2}-17 x-60}{x^{2}+8 x+15}\)
15. \(h(x)=\frac{x^{3}-4 x^{2}-19 x-14}{x^{2}-6 x-7}\)

