3.1: Exponential Functions
- Page ID
- 953
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Exponential growth is one of the most powerful forces in nature. A famous legend states that the inventor of chess was asked to state his own reward from the king. The man asked for a single grain of rice for the first square of the chessboard, two grains of rice for the second square and four grains of rice for the third. He asked for the entire 64 squares to be filled in this way and that would be his reward. Did the man ask for too little, or too much?
Exponential Functions
Exponential functions take the form \(f(x)=a \cdot b^{x}\) where \(a\) and \(b\) are constants. \(a\) is the starting amount when \(x=0 . b\) tells the story about the growth. If the growth is doubling then \(b\) is 2 . If the growth is halving (which would be decay), then \(b\) is \(\frac{1}{2}\). If the growth is increasing by \(6 \%\) then \(b\) is 1.06
Exponential growth is everywhere. Money grows exponentially in banks. Populations of people, bacteria and animals grow exponentially when their food and space aren’t limited.
Radioactive isotopes like Carbon 14 have something called a half-life that indicates how long it takes for half of the molecules present to decay into other more stable molecules. It takes about 5,730 years for this process to occur which is how scientists can date artifacts of ancient humans.
Let's say a mummified animal is found preserved on the slopes of an ice covered mountain. After testing, you see that exactly one fourth of the carbon-14 has yet to decay and you want to find out how long ago was this animal alive. How would you do that?
Since this problem does not give specific amounts of carbon, it can be inferred that the time will not depend on the specific amounts. One technique that makes the problem easier to work with could be to create an example scenario that fits the one fourth ratio. Suppose 60 units were present when the animal was alive at time zero. This means that 15 units must be present today.
\(15=a \cdot\left(\frac{1}{2}\right)^{x}\)
\(60=a \cdot\left(\frac{1}{2}\right)^{0}\)
The second equation yields \(a=60\) and then the first equation becomes:
\(15=60 \cdot\left(\frac{1}{2}\right)^{x}\)
Although you may not yet have the algebraic tools to solve for \(x\), you should still be able to see that \(x\) is \(2 .\) This does not mean that two years ago the animal was alive, it means that two half life cycles ago the animal was alive. The half life cycle for carbon 14 is 5,730 years so this animal was alive over 11,000 years ago.
Now, suppose you invested $100 the day you were born and it grew by 6% every year until you were 100 years old. How would you use an exponential function to determine how much would this investment be worth then?
The starting amount is 100 and the growth is 1.06 because it grows by \(6 \%\) each year. This is enough information to write an exponential function. The \(x\) stands for time in years and the \(f(x)\) stands for the amount of money in the account. Plugging in to the formula for an exponential function, you will get the equation:
\(f(x)=100 \cdot 1.06^{x}\)
Then, you need to substitute in 100 years for \(x\).
\(f(x)=100 \cdot 1.06^{x}\)
\(f(x)=100 \cdot 1.06^{100}\)
\(f(x) \approx 33,930.21\)
After a century, there will be almost $34,000 in the account. Interest has greatly increased the $100 initial investment.
Examples
Earlier you were asked if the man asked for too little or too much rice if he gets one grain for the first square, two grains for the second, four grains for the third and so on. The number of grains of rice on the last square, the 64th square, would be almost ten quintillion (million million million). That is more rice than is produced in the world in an entire year.
\(2^{63}=9,223,372,036,854,775,808\)
Suppose forty rabbits are released on an island. The rabbits mate once every four months and produce up to 4 offspring who also produce more offspring four months later. Estimate the number of rabbits on the island in 3 years if their population grows exponentially. Assume half the population is female.
Even though parts of this problem are unrealistic, it serves to illustrate how quickly exponential growth works. Forty is the initial amount so \(a=40\). At the end of the first 4 month period 20 female rabbits could have their litters and up to 80 newborn rabbits could be born. The population has grown from 40 to 120 which means tripled. Thus, \(b=3\). The last thing to remember is that the time period is in 4 month periods. Three years must be 9 periods.
\(f(x)=40 \cdot 3^{9}=787,320\)
So after three years, there could be up to 787,320 rabbits!
Completely analyze the following exponential function.
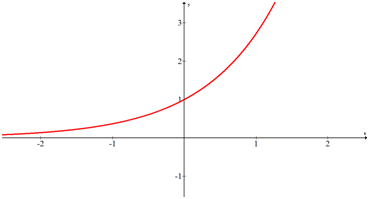
\(f(x)=e^{x}\)
Analyze in this context means to define all the characteristics of a function.
Domain: \(x \in(-\infty, \infty)\)
Range: \(y \in(0, \infty)\)
Increasing: \(x \in(-\infty, \infty)\)
Decreasing: NA
Zeroes: None
Intercepts: (0,1)
Maximums: None
Minimums: None
Asymptotes: \(y=0\) as \(x\) gets infinitely small (Horizontal asymptote)
Holes: None
Identify which of the following functions are exponential functions and which are not.
1. \(y=x^{6}\)
2. \(y=5^{x}\)
3. \(y=1^{x}\)
4. \(y=x^{x}\)
5. \(y=x^{\frac{1}{2}}\)
Exponential functions are of the form \(y=a \cdot b^{x}\)
a. \(y=x^{6}\) is not an exponential function because \(x\) is not in the exponent.
b. \(y=5^{x}\) Exponential function.
c. \(y=1^{x}\) Not a true exponential function because \(y\) is always 1 which is a constant function.
d. \(y=x^{x}\) Not an exponential function because \(x\) is both the base and power of the exponent.
e. \(y=x^{\frac{1}{2}}\) Not an exponential function.
Write the exponential function that passes through the following points: \((0,3),\left(1, \frac{3}{e}\right)\)
The starting number is \(a=3\). This number is changed by a factor of \(\frac{1}{e}\) which is \(b\).
\(f(x)=3\left(\frac{1}{e}\right)^{x}=3 e^{-x}\)
Review
1. Explain what makes a function an exponential function. What does its equation look like?
2. Is the domain for all exponential functions all real numbers?
3. How can you tell from its equation whether or not the graph of an exponential function will be increasing?
4. How can you tell from its equation whether or not the graph of an exponential function will be decreasing?
5. What type of asymptotes do exponential functions have? Explain.
6. Suppose you invested $4,500 and it grew by 4% every year for 30 years. How much would this investment be worth after 30 years?
7. Suppose you invested $10,000 and it grew by 12% every year for 40 years. How much would this investment be worth after 40 years?
Write the exponential function that passes through the following points.
8. (0, 5) and (1, 25)
9. (0, 2) and (1, 8)
10. (0, 16) and (2, 144)
11. (1, 4) and (3, 36)
12. (0, 16) and (3, 2)
13. (0, 81) and (2, 9)
14. (1, 144) and (3, 12)
15. Explain why for exponential functions of the form \(y=a \cdot b^{x}\) the \(y\) -intercept is always the value of
\(a\)