4.3: Special Right Triangles
- Page ID
- 965
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Pythagorean Theorem is great for finding the third side of a right triangle when you already know two other sides. There are some triangles like 30-60-90 and 45-45-90 triangles that are so common that it is useful to know the side ratios without doing the Pythagorean Theorem each time. Using these patterns also allows you to totally solve for the missing sides of these special triangles when you only know one side length.
Given a 45-45-90 right triangle with sides 6 inches, 6 inches and \(x\) inches, what is the value of \(x\) ?
Special Right Triangles
There are three types of special right triangles, 30-60-90 triangles, 45-45-90 triangles, and Pythagorean triple triangles.
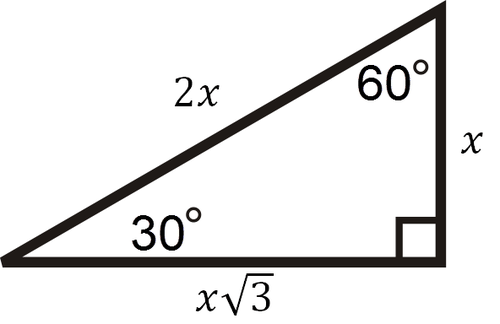
30-60-90 Triangles
A 30-60-90 right triangle has side ratios \(x, x \sqrt{3}, 2 x\).
Confirm with Pythagorean Theorem:
\(\begin{aligned} x^{2}+(x \sqrt{3})^{2} &=(2 x)^{2} \\ x^{2}+3 x^{2} &=4 x^{2} \\ 4 x^{2} &=4 x^{2} \end{aligned}\)
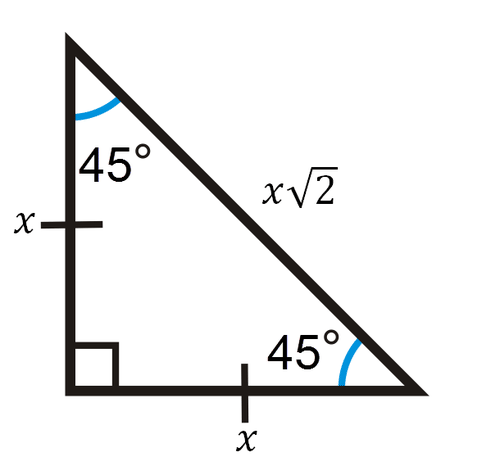
45-45-90 Triangles
A 45 - 45 -90 right triangle has side ratios \(x, x, x \sqrt{2}\).
Confirm with Pythagorean Theorem:
\(\begin{aligned} x^{2}+x^{2} &=(x \sqrt{2})^{2} \\ 2 x^{2} &=2 x^{2} \end{aligned}\)
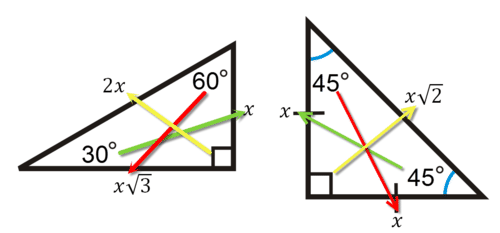
Note that the order of the side ratios \(x, x \sqrt{3}, 2 x\) and \(x, x, x \sqrt{2}\) is important because each side ratio has a corresponding angle. In all triangles, the smallest sides correspond to smallest angles and largest sides always correspond to the largest angles.
Pythagorean Triple Triangles
Pythagorean number triples are special right triangles with integer sides. While the angles are not integers, the side ratios are very useful to know because they show up everywhere. Knowing these number triples also saves a lot of time from doing the Pythagorean Theorem repeatedly. Here are some examples of Pythagorean number triples:
- 3, 4, 5
- 5, 12, 13
- 7, 24, 25
- 8, 15, 17
- 9, 40, 41
More Pythagorean number triples can be found by scaling any other Pythagorean number triple. For example:
\(3,4,5 \rightarrow 6,8,10\) (scaled by a factor of 2)
Even more Pythagorean number triples can be found by taking any odd integer like 11, squaring it to get 121, halving the result to get 60.5. The original number 11 and the two numbers that are 0.5 above and below (60 and 61) will always be a Pythagorean number triple.
\(11^{2}+60^{2}=61^{2}\)
Examples
Earlier you were asked about a 45-45-90 right triangle with sides 6 inches, 6 inches and \(x\) inches. If you can recognize the pattern for 45-45-90 right triangles, a right triangle with legs 6 inches and 6 inches has a hypotenuse that is \(6 \sqrt{2}\) inches \(x=6 \sqrt{2}\).
A 30-60-90 right triangle has hypotenuse of length 10. What are the lengths of the other two sides?
The hypotenuse is the side opposite 90. Sometimes it is helpful to draw a picture or make a table.
| 30 | 60 | 90 |
| \(x\) | \(x \sqrt{3}\) | \(2 x\) |
| 10 |
From the table you can write very small subsequent equations to solve for the missing sides.
\(\begin{aligned} 10 &=2 x \\ x &=5 \\ x \sqrt{3} &=5 \sqrt{3} \end{aligned}\)
The other sides are 5 and \(5 \sqrt{3}\).
A 30-60-90 right triangle has a side length of 18 inches corresponding to 60 degrees. What are the lengths of the other two sides?
Make a table with the side ratios and the information given, then write equations and solve for the missing side lengths.
| 30 | 60 | 90 |
| \(x\) | \(x \sqrt{3}\) | \(2 x\) |
| 18 |
\(\begin{aligned} 18 &=x \sqrt{3} \\ \frac{18}{\sqrt{3}} &=x \\ x &=\frac{18}{\sqrt{3}}=\frac{18}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}}=\frac{18 \sqrt{3}}{3}=6 \sqrt{3} \\ x &=6 \sqrt{3} \end{aligned}\)
Note that you need to rationalize denominators.
Now use the calculated \(x\) value to solve for \(2 x\).
\(2 x=2(6 \sqrt{3})\)
\(2 x=12 \sqrt{3}\)
The other sides are \(6 \sqrt{3}\) and \(12 \sqrt{3}\).
Using your knowledge of special right triangle ratios, solve for the missing sides of the right triangle.
The other sides are each \(\frac{5 \sqrt{2}}{2}\).
| 45 | 45 | 90 |
| \(x\) | \(x\) | \(x \sqrt{2}\) |
| 5 |
\(\begin{aligned} x \sqrt{2} &=5 \\ x &=\frac{5}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}}=\frac{5 \sqrt{2}}{2} \end{aligned}\)
The other sides are each \(\frac{5 \sqrt{2}}{2}\)
Using your knowledge of special right triangle ratios, solve for the missing sides of the right triangle.
The other sides are 9 and \(6 \sqrt{3}\).
| 30 | 60 | 90 |
| \(x\) | \(x \sqrt{3}\) | \(2 x\) |
| \(3 \sqrt{3}\) |
\(\begin{aligned} x &=3 \sqrt{3} \\ 2 x &=6 \sqrt{3} \\ x \sqrt{3} &=3 \sqrt{3} \cdot \sqrt{3}=9 \end{aligned}\)
The other sides are 9 and \(6 \sqrt{3}\).
Review
For 1-4, find the missing sides of the 45-45-90 triangle based on the information given in each row.
| Problem Number | Side Opposite \(45^{\circ}\) | Side Opposite \(45^{\circ}\) | Side Opposite \(90^{\circ}\) |
| 1. | 3 | ||
| 2. | 7.2 | ||
| 3. | 16 | ||
| 4. | \(5 \sqrt{2}\) |
For 5-8, find the missing sides of the 30-60-90 triangle based on the information given in each row.
| Problem Number | Side Opposite \(30^{\circ}\) | Side Opposite \(60^{\circ}\) | Side Opposite \(90^{\circ}\) |
| 1. | \(3 \sqrt{2}\) | ||
| 2. | 4 | ||
| 3. | 15 | ||
| 4. | \(12 \sqrt{3}\) |
Use the picture below for 9-11.
9. Which angle corresponds to the side that is 12 units?
10. Which side corresponds to the right angle?
11. Which angle corresponds to the side that is 5 units?
12. A right triangle has an angle of \(\frac{\pi}{6}\) radians and a hypotenuse of 20 inches. What are the lengths of the other two sides of the triangle?
13. A triangle has two angles that measure \(\frac{\pi}{4}\) radians. The longest side is 3 inches long. What are the lengths of the other two sides?
For 14-19, verify the Pythagorean Number Triple using the Pythagorean Theorem.
14. 3, 4, 5
15. 5, 12, 13
16. 7, 24, 25
17. 8, 15, 17
18. 9, 40, 41
19. 6, 8, 10
20. Find another Pythagorean Number Triple using the method explained for finding “11, 60, 61”.
...