9.5 Hyperbolas
- Page ID
- 1036
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Hyperbolas are relations that have asymptotes. When graphing rational functions you often produce a hyperbola. In this concept, hyperbolas will not be oriented in the same way as with rational functions, but the basic shape of a hyperbola will still be there.
Hyperbolas can be oriented so that they open side to side or up and down. One of the most common mistakes that you can make is to forget which way a given hyperbola should open. What are some strategies to help?
Graphing Hyperbolas
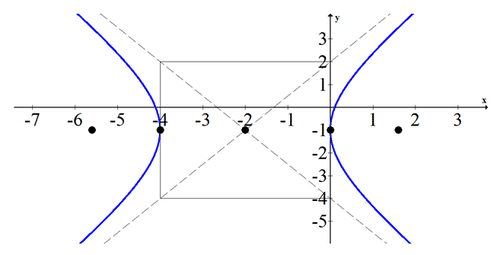
A hyperbola has two foci. For every point on the hyperbola, the difference of the distances to each foci is constant. This is what defines a hyperbola. The graphing form of a hyperbola that opens side to side is:
\(\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1\)
A hyperbola that opens up and down is:
\(\frac{(y-k)^{2}}{a^{2}}-\frac{(x-h)^{2}}{b^{2}}=1\)
Notice that for hyperbolas, \(a\) goes with the positive term and \(b\) goes with the negative term. It does not matter which constant is larger.
When graphing, the constants \(a\) and \(b\) enable you to draw a rectangle around the center. The transverse axis travels from vertex to vertex and has length \(2 a\). The conjugate axis travels perpendicular to the transverse axis through the center and has length \(2 b\). The foci lie beyond the vertices so the eccentricity, which is measured as \(e=\frac{c}{a},\) is larger than 1 for all hyperbolas. Hyperbolas also have two directrix lines that are \(\frac{a^{2}}{c}\) away from the center (not shown on the image).
The focal radius is \(a^{2}+b^{2}=c^{2}\)
Examples
Earlier, you were asked how to determine the direction that a hyperbola opens. The best strategy to remember which direction the hyperbola opens is often the simplest. Consider the hyperbola \(x^{2}-y^{2}=1\). This hyperbola opens side to side because \(x\) can clearly never be equal to zero. This is a basic case that shows that when the negative is with the \(y\) value then the hyperbola opens up side to side.
Put the following hyperbola into graphing form, list the components, and sketch it.
\(9 x^{2}-4 y^{2}+36 x-8 y-4=0\)
\(\begin{aligned} 9\left(x^{2}+4 x\right)-4\left(y^{2}+2 y\right) &=4 \\ 9\left(x^{2}+4 x+4\right)-4\left(y^{2}+2 y+1\right) &=4+36-4 \\ 9(x+2)^{2}-4(y+1)^{2} &=36 \\ \frac{(x+2)^{2}}{4}-\frac{(y+1)^{2}}{9} &=1 \end{aligned}\)
Shape: Hyperbola that opens horizontally.
Center: (-2,-1)
\(a=2\)
\(b=3\)
\(c=\sqrt{13}\)
\(e=\frac{c}{a}=\frac{\sqrt{13}}{2}\)
\(d=\frac{a^{2}}{c}=\frac{4}{\sqrt{13}}\)
Foci: \(\left(-2+\frac{\sqrt{13}}{2},-1\right),\left(-2-\frac{\sqrt{13}}{2},-1\right)\)
Vertices: (-4,-1),(0,-1)
Equations of asymptotes: \(\pm \frac{3}{2}(x+2)=(y+1)\)
Note that it is easiest to write the equations of the asymptotes in point-slope form using the center and the slope.
Equations of directrices: \(y=-2 \pm \frac{4}{\sqrt{13}}\)
Find the equation of the hyperbola with foci at (-3,5) and (9,5) and asymptotes with slopes of \(\pm \frac{4}{3}\).
The center is between the foci at (3,5) . The focal radius is \(c=6\). The slope of the asymptotes is always the rise over run inside the box. In this case since the hyperbola is horizontal and \(a\) is in the \(x\) direction the slope is \(\frac{b}{a}\). This makes a system of equations.
\(\frac{b}{a}=\pm \frac{4}{3}\)
\(a^{2}+b^{2}=6^{2}\)
When you solve,you get \(a=\sqrt{13}, b=\frac{4}{3} \sqrt{13}\).
\(\frac{(x-3)^{2}}{13}-\frac{(y-5)^{2}}{\frac{16}{9} \cdot 13}=1\)
Find the equation of the conic that has a focus point at (1,2) , a directrix at \(x=5\), and an eccentricity equal to \(\frac{3}{2}\). Use the property that the distance from a point on the hyperbola to the focus is equal to the eccentricity times the distance from that same point to the directrix:
\(\overline{P F}=e \overline{P D}\)
This relationship bridges the gap between ellipses which have eccentricity less than one and hyperbolas which have eccentricity greater than one. When eccentricity is equal to one, the
shape is a parabola.
\(\sqrt{(x-1)^{2}+(y-2)^{2}}=\frac{3}{2} \sqrt{(x-5)^{2}}\)
Square both sides and rearrange terms so that it is becomes a hyperbola in graphing form.
\(\begin{aligned} x^{2}-2 x+1+(y-2)^{2} &=\frac{9}{4}\left(x^{2}-10 x+25\right) \\ x^{2}-2 x+1-\frac{9}{4} x^{2}+\frac{90}{4} x-\frac{225}{4}+(y-2)^{2} &=0\\-\frac{5}{4} x^{2}+\frac{92}{4} x+(y-2)^{2} &=\frac{221}{4}\\-5 x^{2}+92 x+4(y-2)^{2} &=221\\-5\left(x^{2}-\frac{92}{5} x\right)+4(y-2)^{2} &=221 \end{aligned}\)
\(\begin{aligned}-5\left(x^{2}-\frac{92}{5} x+\frac{92^{2}}{10^{2}}\right)+4(y-2)^{2} &=221-\frac{2116}{5}\\-5\left(x-\frac{92}{10}\right)^{2}+4(y-2)^{2} &=-\frac{1011}{5} \\\left(x-\frac{92}{10}\right)^{2}-(y-2)^{2} &=\frac{1011}{100} \\ \frac{\left(x-\frac{92}{10}\right)^{2}}{\left(\frac{1011}{100}\right)}-\frac{(y-2)^{2}}{\left(\frac{1011}{100}\right)} &=1 \end{aligned}\)
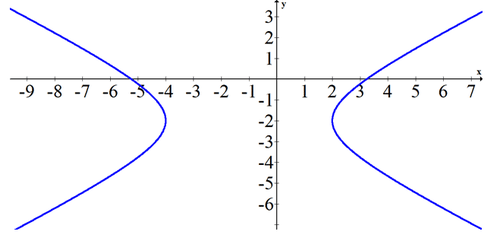
Given the following graph, estimate the equation of the conic.
Since exact points are not marked, you will need to estimate the slope of asymptotes to get an approximation for \(a\) and \(b\). The slope seems to be about \(\pm \frac{2}{3}\). The center seems to be at \((-1\), -2). The transverse axis is 6 which means \(a=3\).
\(\frac{(x+1)^{2}}{9}-\frac{(y+2)^{2}}{4}=1\)
Use the following equation for #1-#5: \(x^{2}+2 x-4 y^{2}-24 y-51=0\)
1. Put the hyperbola into graphing form. Explain how you know it is a hyperbola.
2. Identify whether the hyperbola opens side to side or up and down.
3. Find the location of the vertices.
4. Find the equations of the asymptotes.
5. Sketch the hyperbola.
Use the following equation for \(\# 6-\# 10:-9 x^{2}-36 x+16 y^{2}-32 y-164=0\)
6. Put the hyperbola into graphing form. Explain how you know it is a hyperbola.
7. Identify whether the hyperbola opens side to side or up and down.
8. Find the location of the vertices.
9. Find the equations of the asymptotes.
10. Sketch the hyperbola.
Use the following equation for #11 - #15: \(x^{2}-6 x-9 y^{2}-54 y-81=0\)
11. Put the hyperbola into graphing form. Explain how you know it is a hyperbola.
12. Identify whether the hyperbola opens side to side or up and down.
13. Find the location of the vertices.
14. Find the equations of the asymptotes.
15. Sketch the hyperbola.