Skip to main content
K12 LibreTexts

2.7.2: Linear Regression Equations

  1. Last updated
  2. Save as PDF
  • Page ID
    5771

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Linear Regression Equations 

    Scatter plots and lines of best fit can also be drawn by using technology. The TI-83 is capable of graphing both a scatter plot and of inserting the line of best fit onto the scatter plot. The calculator is also able to find the correlation coefficient (r) and the coefficient of determination (r2) for the linear regression equation.

    The correlation coefficient will have a value between −1 and 1. The closer the correlation coefficient is to −1 or 1, the stronger the correlation. If the correlation coefficient is negative, this implies a negative correlation, and if the correlation coefficient is positive, this implies a positive correlation. The coefficient of determination is just the correlation coefficient squared, and, therefore, it is always positive. The closer the coefficient of determination is to 1, the stronger the correlation.

    Creating a Scatter plot Using a Calculator

    The following table consists of the marks achieved by 9 students on chemistry and math tests. Create a scatter plot for the data with your calculator.

    Student A B C D E F G H I
    Chemistry Marks 49 46 35 58 51 56 54 46 53
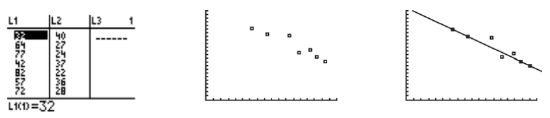
    Math Marks 29 23 10 41 38 36 31 24 ?

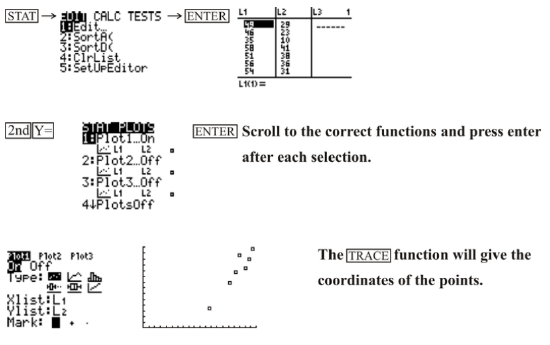
    Screen Shot 2020-05-12 at 10.36.52 PM.png

    Drawing a Line of Best Fit 

    Draw a line of best fit for the data that you plotted in the previous example. Use the line of best fit to calculate the predicted value for Student I's math test mark.

    The calculator can now be used to determine a linear regression equation for the given values. The equation can be entered into the calculator, and the line will be plotted on the scatter plot.

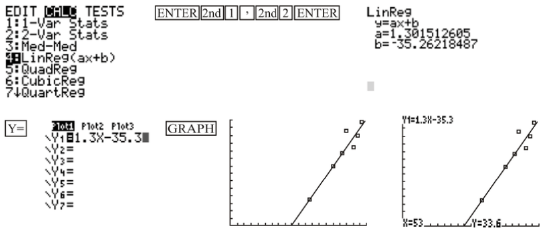
    Screen Shot 2020-05-12 at 10.37.18 PM.png

    From the line of best fit, the calculated value for Student I's math test mark is 33.6.

    Determining the Correlation Coefficient and the Coefficient of Determination 

    Determine the correlation coefficient and the coefficient of determination for the linear regression equation that you found in Example B. Is the linear regression equation a good fit for the data?

    The correlation coefficient and the coefficient of determination for the linear regression equation are found the same way that the linear regression equation is found. In other words, to find the correlation coefficient and the coefficient of determination, after entering the data into your calculator, press STAT, go to the CALC menu, and choose LinReg(ax + b). After pressing ENTER to choose LinReg(ax + b), press ENTER again, and you should see the following screen:

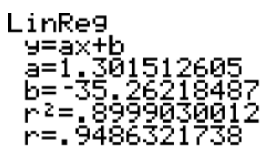
    Screen Shot 2020-05-12 at 10.38.18 PM.png

    You can see that r, or the correlation coefficient, is equal to 0.9486321738, while r2, or the coefficient of determination, is equal to 0.8999030012. This means that the linear regression equation is a moderately good fit, but not a great fit, for the data.

    Examples

    The data below gives the fuel efficiency of cars with the same-sized engines when driven at various speeds.

    Screen Shot 2020-05-12 at 10.39.33 PM.png

    Screen Shot 2020-05-12 at 10.39.37 PM.png

    Example 1

    Draw a scatter plot and a line of best fit using technology. What is the equation of the line of best fit?

    Screen Shot 2020-05-12 at 10.40.59 PM.png

    From the following screen, the equation of the line of best fit is approximately y=−0.36x+52.6.

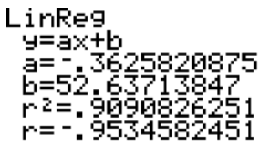
    Screen Shot 2020-05-12 at 10.41.25 PM.png

    Example 2

    What is the correlation coefficient and the coefficient of determination of the linear regression equation? Is the linear regression equation a good fit for the data?

    As can be seen in the screen in the answer to part a, the correlation coefficient is 0.9534582451, while the coefficient of determination is 0.9090826251. This means that the linear regression equation is a moderately good fit, but not a great fit, for the data.

    Example 3

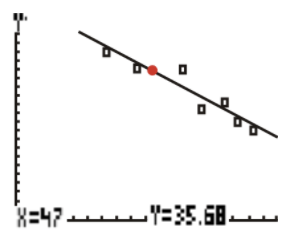
    If a car were traveling at a speed of 47 m/h, estimate the fuel efficiency of the car. 

    Using the TI-83 to calculate the value, the fuel efficiency of a car traveling at a speed of 47 m/h would be approximately 35 m\gal.

    Screen Shot 2020-05-12 at 10.43.43 PM.png

    Example 4

    If a car has a fuel efficiency of 29 m/gal, estimate the speed of the car. 

    From the calculator, the equation of the line of best fit is approximately y=−0.36x+52.6, where y represents the fuel efficiency of the car and x represents the speed of the car.

    Using this equation:


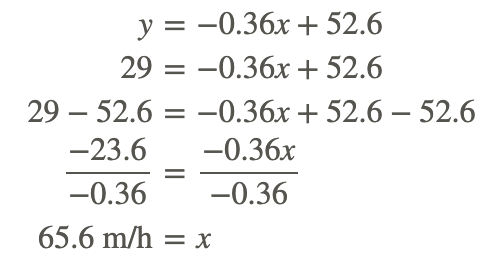
    Screen Shot 2020-05-12 at 10.44.11 PM.png

    The speed of the car would be approximately 65.6 miles per hour.

    Review 

    1. Which of the following calculations will create the line of best fit on the TI-83?
      1. quadratic regression
      2. cubic regression
      3. exponential regression
      4. linear regression (ax+b)

    The linear regression below was performed on a data set with a TI calculator. Use the information shown on the screen to answer the following questions:

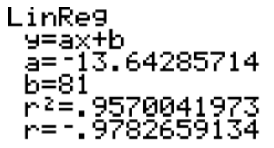
    Screen Shot 2020-05-12 at 10.44.45 PM.png

    1. What is the linear regression equation?
    2. What is the correlation coefficient and the coefficient of determination? Is the linear regression equation a good fit for the data?
    3. According to the linear regression equation, what would be the approximate value of y when x = 3?

    The linear regression below was performed on a data set with a TI calculator. Use the information shown on the screen to answer the following questions:

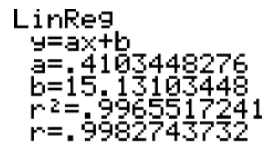
    Screen Shot 2020-05-12 at 10.45.59 PM.png

    1. What is the linear regression equation?
    2. What is the correlation coefficient and the coefficient of determination? Is the linear regression equation a good fit for the data?
    3. According to the linear regression equation, what would be the approximate value of x when y = 8?

    Review 

    To view the Review answers, open this PDF file and look for section 7.4. 

    Vocabulary

    Term Definition
    correlation coefficient (r) and the coefficient of determination (r2) are both standard quantitative measures of best fit. The correlation coefficient has values from −1 to 1, and the closer the value is to −1 or 1, the better the fit. If the correlation coefficient is negative, the correlation is negative, and if it is positive, the correlation is positive. The coefficient of determination is the correlation coefficient squared and has values from 0 to 1. The closer the value is to 1, the better the fit.
    coefficient of determination The coefficient of determination is the square of the correlation coefficient and therefore has values from 0 to 1.
    correlation coefficient The correlation coefficient is a standard quantitative measure of best fit of a line. It has the symbol r and has values from -1 to +1.

    This page titled 2.7.2: Linear Regression Equations is shared under a CC BY-NC license and was authored, remixed, and/or curated by CK-12 Foundation via source content that was edited to the style and standards of the LibreTexts platform.