3.4: Planning and Conducting Surveys
- Page ID
- 5708
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Designing, Conducting, and Analyzing Surveys
A survey is a way to ask a lot of people a few well-constructed questions. The survey is a series of unbiased questions that the subject must answer. Some advantages of surveys are that they are efficient ways of collecting information from a large number of people, they are relatively easy to administer, a wide variety of information can be collected and they can be focused (researchers can stick to just the questions that interest them.) Some disadvantages of surveys arise from the fact that they depend on the subjects’ motivation, honesty, memory and ability to respond. Moreover, answer choices to survey questions could lead to vague data. For example, the choice “moderately agree” may mean different things to different people or to whoever ends up interpreting the data.
Conducting a Survey
There are various methods for administering a survey. It can be done as a face-to face interview or a phone interview where the researcher is questioning the subject. A different option is to have a self-administered survey where the subject can complete a survey on paper and mail it back, or complete the survey online. There are advantages and disadvantages to each of these methods.
The advantages of face-to-face interviews include fewer misunderstood questions, fewer incomplete responses, higher response rates, and greater control over the environment in which the survey is administered; also, the researcher can collect additional information if any of the respondents’ answers need clarifying. The disadvantages of face-to-face interviews are that they can be expensive and time-consuming and may require a large staff of trained interviewers. In addition, the response can be biased by the appearance or attitude of the interviewer.
The advantages of self-administered surveys are that they are less expensive than interviews, do not require a large staff of experienced interviewers and can be administered in large numbers. In addition, anonymity and privacy encourage more candid and honest responses, and there is less pressure on respondents. The disadvantages of self-administered surveys are that responders are more likely to stop participating mid-way through the survey and respondents cannot ask them to clarify their answers. In addition, there are lower response rates than in personal interviews, and often the respondents who bother to return surveys represent extremes of the population – those people who care about the issue strongly, whichever way their opinion leans.
Designing a Survey
Surveys can take different forms. They can be used to ask only one question or they can ask a series of questions. We can use surveys to test out people’s opinions or to test a hypothesis.
When designing a survey, the following steps are useful:
- Determine the goal of your survey: What question do you want to answer?
- Identify the sample population: Whom will you interview?
- Choose an interviewing method: face-to-face interview, phone interview, self-administered paper survey, or internet survey.
- Decide what questions you will ask in what order, and how to phrase them. (This is important if there is more than one piece of information you are looking for.)
- Conduct the interview and collect the information.
- Analyze the results by making graphs and drawing conclusions.
Constructing a Survey
1. Martha wants to construct a survey that shows which sports students at her school like to play the most.
a) List the goal of the survey.
The goal of the survey is to find the answer to the question: “Which sports do students at Martha’s school like to play the most?”
b) What population sample should she interview?
A sample of the population would include a random sample of the student population in Martha’s school. A good strategy would be to randomly select students (using dice or a random number generator) as they walk into an all-school assembly.
c) How should she administer the survey?
Face-to-face interviews are a good choice in this case. Interviews will be easy to conduct since the survey consists of only one question which can be quickly answered and recorded, and asking the question face to face will help eliminate non-response bias.
d) Create a data collection sheet that she can use to record her results.
In order to collect the data to this simple survey Martha can design a data collection sheet such as the one below:
| Sport | Tally |
|---|---|
| baseball | |
| basketball | |
| football | |
| soccer | |
| volleyball | |
| swimming |
This is a good, simple data collection sheet because:
- Plenty of space is left for the tally marks.
- Only one question is being asked.
- Many possibilities are included, but space is left at the bottom in case students give answers that Martha didn’t think of.
- The answer from each interviewee can be quickly collected and then the data collector can move on to the next person.
Once the data has been collected, suitable graphs can be made to display the results.
2. Raoul wants to construct a survey that shows how many hours per week the average student at his school works.
a) List the goal of the survey.
The goal of the survey is to find the answer to the question “How many hours per week do you work?”
b) What population sample will he interview?
Raoul suspects that older students might work more hours per week than younger students. He decides that a stratified sample of the student population would be appropriate in this case. The strata are grade levels 9th through 12th. He would need to find out what proportion of the students in his school are in each grade level, and then include the same proportions in his sample.
c) How would he administer the survey?
Face-to-face interviews are a good choice in this case since the survey consists of two short questions which can be quickly answered and recorded.
d) Create a data collection sheet that Raoul can use to record his results.
In order to collect the data for this survey Raoul designed the data collection sheet shown below:
| Grade Level | Number of Hours Worked | Total number of students |
|---|---|---|
| 9th grade | ||
| 10th grade | ||
| 11th grade | ||
| 12th grade |
This data collection sheet allows Raoul to write down the actual numbers of hours worked per week by students as opposed to just collecting tally marks for several categories.
Display, Analyze, and Interpret Statistical Survey Data
In the previous section we considered two examples of surveys you might conduct in your school. The first one was designed to find the sport that students like to play the most. The second survey was designed to find out how many hours per week students worked.
For the first survey, students’ choices fit neatly into separate categories. Appropriate ways to display the data might be a pie chart or a bar graph. Let’s revisit this example.
In Example A Martha interviewed 112 students and obtained the following results.
| Sport | Tally | |
|---|---|---|
| baseball | 31 | |
| basketball | 17 | |
| football | 14 | |
| soccer | 28 | |
| volleyball | 9 | |
| swimming | 8 | |
| gymnastics | ||| | 3 |
| fencing | || | 2 |
| Total: 112 |
a) Make a bar graph of the results showing the percentage of students in each category.
To make a bar graph, we list the sport categories on the x−axis and let the percentage of students be represented by the y−axis.
To find the percentage of students in each category, we divide the number of students in each category by the total number of students surveyed:
| Sport | Percentage |
|---|---|
| baseball | 31/112=.28=28% |
| basketball | 17/112=.15=15% |
| football | 14/112=.125=12.5% |
| soccer | 28/112=.25=25% |
| volleyball | 91/12=.08=8% |
| swimming | 8/112=.07=7% |
| gymnastic | 3/112=.025=2.5% |
| fencing | 2/112=.02=2% |
Now we can make a graph where the height of each bar represents the percentage of students in each category:
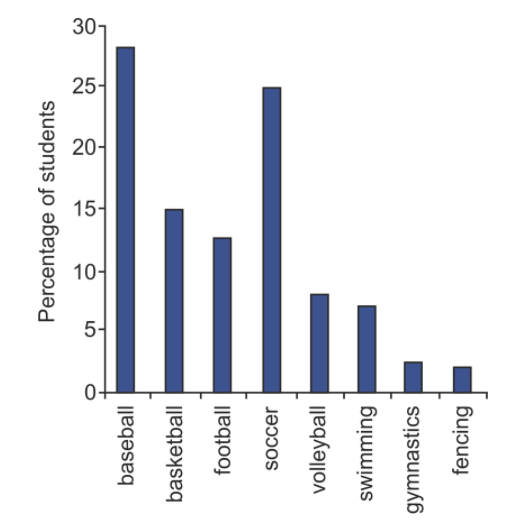
b. Make a pie chart of the collected information, showing the percentage of students in each category.
To make a pie chart, we find the percentage of the students in each category by dividing the number of students in each category as in part a. The central angle of each slice of the pie is found by multiplying the percentage of students in each category by 360 degrees (the total number of degrees in a circle). To draw a pie-chart by hand, you can use a protractor to measure the central angles that you find for each category.
| Sport | Percentage | Central angle |
|---|---|---|
| baseball | 31/112=.28=28% | .28×360∘=101∘ |
| basketball | 17/112=.15=15% | .15×360∘=54∘ |
| football | 14/112=.125=12.5% | .125×360∘=45∘ |
| soccer | 28/112=.25=25% | .25×360∘=90∘ |
| volleyball | 91/12=.08=8% | .08×360∘=29∘ |
| swimming | 8/112=.07=7% | .07×360∘=25∘ |
| gymnastics | 3/112=.025=2.5% | .025×360∘=9∘ |
| fencing | 2/112=.02=2% | .02×360∘=7∘ |
Here is the pie-chart that represents the percentage of students in each category:
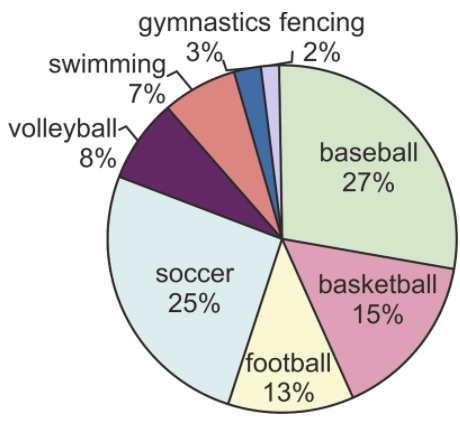
For the second survey, actual numerical data can be collected from each student. In this case we can display the data using a stem-and-leaf plot, a frequency table, a histogram, or a box-and-whisker plot.
Examples
In the second example Raoul found that that 30% of the students at his school are in 9th grade, 26% of the students are in the 10th grade, 24% of the students are in 11th grade and 20% of the students are in the 12th grade. He surveyed a total of 60 students using these proportions as a guide for the number of students he interviewed from each grade. Raoul recorded the following data:
| Grade Level | Number of hours worked | Total number of students |
|---|---|---|
| 9th grade |
0, 5, 4, 0, 0, 10, 5, 6, 0, 0, 2, 4, 0, 8, 0, 5, 7, 0 |
18 |
| 10th grade |
6, 10, 12, 0, 10, 15, 0, 0, 8, 5, 0, 7, 10, 12, 0, 0 |
16 |
| 11th grade |
0, 12, 15, 18, 10, 0, 0, 20, 8, 15, 10, 15, 0, 5 |
14 |
| 12th grade |
22, 15, 12, 15, 10, 0, 18, 20, 10, 0, 12, 16 |
12 |
Example 1
Construct a stem-and-leaf plot of the collected data
The ordered stem-and-leaf plot looks as follows:
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 4 4 5 5 5 5 5 6 6 7 7 8 8 8
1 0 0 0 0 0 0 0 0 2 2 2 2 2 5 5 5 5 5 5 6 8 8
2 0 0 2
We can easily see from the stem-and-leaf plot that the mode of the data is 0. This makes sense because many students do not work in high school.
Example 2
Construct a frequency table with bin size of 5.
We construct the frequency table by counting how many students fit in each category.
| Hours worked | Frequency |
|---|---|
| 0≤x<5 | 23 |
| 5≤x<10 | 12 |
| 10≤x<15 | 13 |
| 15≤x<20 | 9 |
| 20≤x<25 | 3 |
Example 3
Draw a histogram of the data.
The histogram associated with this frequency table is shown below.
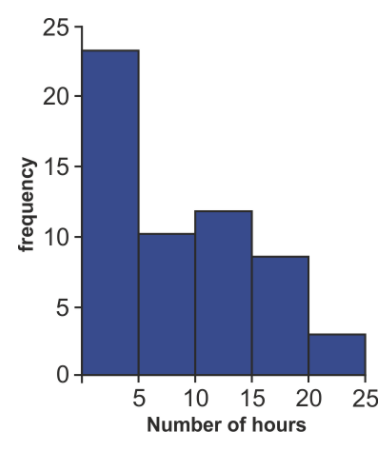
Example 4
Find the five number summary of the data and draw a box-and-whisker plot.
The five number summary is as follows:
smallest number = 0
largest number = 22
Since there are 60 data points, (n+12)=30.5. The median is the mean of the 30th and the 31st values:
median = 6.5
Since each half of the list has 30 values in it, then the first and third quartiles are the medians of each of the smaller lists. The first quartile is the mean of the 15th and 16th values:
first quartile = 0
The third quartile is the mean of the 45th and 46th values:
third quartile = 12
The associated box-and-whisker plot is shown below.

Review
- Make a pie chart for the problem in the Guided Practice. Specifically a total of 60 students in four groups composed of: 18 ninth grade students, 16 tenth grade students, 14 eleventh grade students, and 12 twelfth grade students.
- Melissa conducted a survey to answer the question “What sport do high school students like to watch on TV the most?” She collected the following information on her data collection sheet.
| Sport | Tally | |
|---|---|---|
| baseball | 32 | |
| basketball | 28 | |
| football | 24 | |
| soccer | 18 | |
| gymnastics | 19 | |
| figure skating | 8 | |
| hockey | 18 | |
| Total: | 147 |
a) Make a pie-chart of the results showing the percentage of people in each category.
b) Make a bar-graph of the results.
- Samuel conducted a survey to answer the following question: “What is the favorite kind of pie of the people living in my town?” By standing in front of his grocery store, he collected the following information on his data collection sheet:
| Type of pie | Tally | |
|---|---|---|
| apple | 37 | |
| pumpkin | 13 | |
| lemon meringue | 7 | |
| chocolate mousse | 23 | |
| cherry | |||| | 4 |
| chicken pot pie | 31 | |
| other | 7 | |
| Total: | 122 |
a) Make a pie chart of the results showing the percentage of people in each category.
b) Make a bar graph of the results.
- Myra conducted a survey of people at her school to see “In which month does a person’s birthday fall?” She collected the following information in her data collection sheet:
| Month | Tally | |
|---|---|---|
| January | 16 | |
| February | 13 | |
| March | 12 | |
| April | 11 | |
| May | 13 | |
| June | 12 | |
| July | 9 | |
| August | 7 | |
| September | 9 | |
| October | 8 | |
| November | 13 | |
| December | 13 | |
| Total: | 136 |
a) Make a pie chart of the results showing the percentage of people whose birthday falls in each month.
b) Make a bar graph of the results.
- Nam-Ling conducted a survey that answers the question “Which student would you vote for in your school’s elections?” She collected the following information:
| Candidate | 9th graders | 10th graders | 11th graders | 12th graders | Total |
|---|---|---|---|---|---|
| Susan Cho | || | | | 19 | ||
| Margarita Martinez | |||| | 31 | |||
| Steve Coogan | |||| | || | 16 | ||
| Solomon Duning | | | | | 26 | ||
| Juan Rios | ||| | 28 | |||
| Total | 36 | 30 | 30 | 24 | 120 |
a) Make a pie chart of the results showing the percentage of people planning to vote for each candidate.
b) Make a bar graph of the results.
- Graham conducted a survey to find how many hours of TV teenagers watch each week in the United States. He collaborated with three friends that lived in different parts of the US and found the following information:
| Part of the country | Number of hours of TV watched per week | Total number of teens |
|---|---|---|
| West Coast | 10, 12, 8, 20, 6, 0, 15, 18, 12, 22, 9, 5, 16, 12, 10, 18, 10, 20, 24, 8 | 20 |
| Mid West | 20, 12, 24, 10, 8, 26, 34, 15, 18, 6, 22, 16, 10, 20, 15, 25, 32, 12, 18, 22 | 20 |
| New England | 16, 9, 12, 0, 6, 10, 15, 24, 20, 30, 15, 10, 12, 8, 28, 32, 24, 12, 10, 10 | 20 |
| South | 24, 22, 12, 32, 30, 20, 25, 15, 10, 14, 10, 12, 24, 28, 32, 38, 20, 25, 15, 12 | 20 |
a) Make a stem-and-leaf plot of the data.
b) Decide on an appropriate bin size and construct a frequency table.
c) Make a histogram of the results.
d) Find the five-number summary of the data and construct a box-and-whisker plot.
In exercises 7-10, consider the following survey questions.
- “What do students in your high-school like to spend their money on?”
- Which categories would you include on your data collection sheet?
- Design the data collection sheet that can be used to collect this information.
- Conduct the survey. This activity is best done as a group with each person contributing at least 20 results.
- Make a pie chart of the results showing the percentage of people in each category.
- Make a bar graph of the results.
- “What is the height of students in your class?”
- Design the data collection sheet that can be used to collect this information.
- Conduct the survey. This activity is best done as a group with each person contributing at least 20 results.
- Make a stem-and-leaf plot of the data.
- Decide on an appropriate bin size and construct a frequency table.
- Make a histogram of the results.
- Find the five-number summary of the data and construct a box-and-whisker plot.
- “How much allowance money do students in your school get per week?”
- Design the data collection sheet that can be used to collect this information,
- Conduct the survey. This activity is best done as a group with each person contributing at least 20 results.
- Make a stem-and-leaf plot of the data.
- Decide on an appropriate bin size and construct a frequency table.
- Make a histogram of the results.
- Find the five-number summary of the data and construct a box-and-whisker plot.
- “What time do students in your school get up in the morning during the school week?”
- Design the data collection sheet that can be used to collect this information.
- Conduct the survey. This activity is best done as a group with each person contributing at least 20 results.
- Make a stem-and-leaf plot of the data.
- Decide on an appropriate bin size and construct a frequency table.
- Make a histogram of the results.
- Find the five-number summary of the data and construct a box-and-whisker plot.
Vocabulary
| Term | Definition |
|---|---|
| Frequency table | A frequency table is a table that summarizes a data set by stating the number of times each value occurs within the data set. |
| pie chart | A pie chart shows the relationship of the parts to the whole by visually comparing the sizes of the sections (slices) of a circle. |
Additional Resources
Video: Designing, Conducting and Analyzing Surveys: A Sample Application
Practice: Planning and conducting Surveys
Real World: Red States, Blue States

