7.9: Relative Frequency Interpretation
- Page ID
- 5742
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A school lunch break is divided into multiple sessions, the 1st group, consisting of 20 girls and 50 boys, begins lunch at 11:30 am, the 2nd group, with 35 girls and 30 boys begins at 11:40, and the 3rd group, 40 girls and 25 boys, at 11:50.
Assuming that none of the students from an early group leave the cafeteria before everyone goes back to class at 12:10, what is the relative frequency of girls in the cafeteria at 11:35? What about at 11:45? 11:55?
In this lesson we discuss cumulative frequencies, and by the end of the lesson, this sort of question will be no problem at all.
Cumulative Frequencies
Cumulative frequencies describe a sort of ‘running total’ of frequencies in a frequency distribution. You will find cumulative frequencies in many real-world situations, since we often need to collect data for a larger study by conducting several smaller studies.
To calculate a cumulative frequency, simply create a frequency distribution table, then add the frequency from the first category to that of the second category, then add that total frequency to the third category, and so on. Because cumulative distributions don’t generally show different combinations of categories, it is a good idea to arrange your categories in a suitable order so that the cumulative frequencies are most likely to be of use as the running total increases.
A relative cumulative frequency table shows how the cumulative frequency after each successive interval compares to the total frequency. To create a relative cumulative frequency table, calculate the relative frequency of each interval or category, and then add the relative frequency of each category to all the prior ones.
Creating a Cumulative Frequency Table
Create a cumulative frequency table showing the number of hours per week that Brian watches television, based on the given information.
Brian’s T.V. Time

flash.pro - www.flickr.com/photos/flashpro/4156535452
- Monday: 1.5 hrs
- Tuesday: 2.25 hrs
- Wednesday: 2 hrs
- Thursday: 1.75 hrs
- Friday: 1.5 hrs
- Saturday: 3.25 hrs
- Sunday: 2.5 hrs
To find the cumulative frequency of hours of T.V. watched, add the frequency of each day to the total frequency of the day before:
| Day | Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday |
| Cumulative Frequency | 1.5 hrs | 1.5 + 2.25 = 3.75 hrs | 3.75 + 2 = 5.75 hrs | 5.75 + 1.75 = 7.5 hrs | 7.5 + 1.5 = 9 hrs | 9 + 3.25 = 12.25 hrs | 12.25 + 2.5 = 15 hrs |
Creating a Relative Cumulative Frequency Table
A car dealer is calculating the total sales for the past month, and wants to identify the percentage of monthly sales that have occurred after weeks 1, 2, 3, and 4. Create a relative cumulative frequency table to show the information the dealer wants.
| Week Number | Cars Sold |
| 1 | 21 |
| 2 | 12 |
| 3 | 17 |
| 4 | 24 |
First total up the sales for the entire month:
21+12+17+24=74 cars
Then find the relative frequencies for each week by dividing the number of cars sold that week by the total:
- The relative frequency for the first week is: 21/74=.284
- The relative frequency for the second week is: 12/74=.162
- The relative frequency for the third week is: 17/74=.23
- The relative frequency for the fourth week is: 24/74=.324
To find the relative cumulative frequencies, start with the frequency for week 1 and for each successive week, total all of the previous frequencies:
| Week Number | Cars Sold | Relative Frequency | Cumulative Frequency |
| 1 | 21 | .284 | .284 |
| 2 | 12 | .162 | .284+.162=.446 |
| 3 | 17 | .23 | .446+.23=.676 |
| 4 | 24 | .324 | .676+.324=1.0 |

Daniel Oines - www.flickr.com/photos/dno1967b/5543841808
Note that the first relative cumulative frequency is always the same as the first relative frequency, and the last relative cumulative frequency is always equal to 1.
Constructing Tables
Create a cumulative and relative cumulative frequency table for the following data:
Number of customers in store on Black Friday each year for the years 1995 – 2005:
47, 49, 48, 54, 57, 52, 61, 65, 67, 66, 70
Label a table with the years 1995 - 2005 across the top and frequency, cumulative frequency, and relative cumulative frequency down the side. Leave 3 blanks underneath each year, and input the frequency for each year:
| Year: | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 |
| Frequency | 47 | 49 | 48 | 54 | 57 | 52 | 61 | 65 | 67 | 66 | 70 |
|
Cumulative Frequency |
|||||||||||
|
Relative Cumulative Frequency |
To calculate the cumulative frequencies, sum the total of all previous frequencies under the frequency for each year:
| Year | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 |
| Frequency | 47 | 49 | 48 | 54 | 57 | 52 | 61 | 65 | 67 | 66 | 70 |
|
Cumulative Frequency |
47 | 96 | 144 | 198 | 255 | 307 | 368 | 433 | 500 | 566 | 636 |
|
Relative Cumulative Frequency |
To calculate the relative cumulative frequencies, divide the cumulative frequency for each year by the total cumulative frequency (636 customers, the same as the value for the last year, 2005).
| Year | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 |
| Frequency | 47 | 49 | 48 | 54 | 57 | 52 | 61 | 65 | 67 | 66 | 70 |
|
Cumulative Frequency |
47 | 96 | 144 | 198 | 255 | 307 | 368 | 433 | 500 | 566 | 636 |
|
Relative Cumulative Frequency |
.074 | .151 | .226 | .311 | .401 | .483 | .579 | .681 | .786 | .890 | 1.0 |
Earlier Problem Revisited
A school lunch break is divided into multiple sessions, the 1st group, consisting of 20 girls and 50 boys, begins lunch at 11:30 am, the 2nd group, with 35 girls and 30 boys begins at 11:40, and the 3rd group, 40 girls and 25 boys, at 11:50.
Assuming that none of the students from an early group leave the cafeteria before everyone goes back to class at 12:10, what is the relative frequency of girls in the cafeteria at 11:35? What about at 11:45? 11:55?
First create a table showing each session and the number of boys and girls in each session:
| Session 1 - 11:30 | Session 2 - 11:40 | Session 3 - 11:50 | |||
| Boys | Girls | Boys | Girls | Boys | Girls |
| 50 | 20 | 30 | 35 | 25 | 40 |
Next, add a row to the bottom of your table for cumulative relative frequency of girls:
| Session 1 | Session 2 | Session 3 | |||
| Boys | Girls | Boys | Girls | Boys | Girls |
| 50 | 20 | 30 | 35 | 25 | 40 |
| Girls: 2070=.286 or 28.6 % | Girls: 55135=.407 or 40.7% | Girls: 95200=.475 or 47.5% |
Examples
For 25 days, the snow depth at Whiteout Mountain was measured (to the nearest inch) and recorded as follows:
242, 228, 217, 253, 239, 266, 242, 251, 240, 223, 219, 246, 260, 258, 225, 234, 230, 249, 245, 254, 243, 235, 231, 257
- Determine a reasonable class interval
- Set up a frequency distribution table
- Find the frequency for each class interval
- Calculate the cumulative frequencies progressively from left to right
- Use the information gathered from the frequency distribution table to plot a cumulative frequency graph.
Solutions:
Example 1
Determine a reasonable class interval
The values range 217 – 266, a class interval of 10 would break the data up into a reasonable 6 bins.
Example 2
Set up a frequency distribution table, and find the frequency for each class interval
Create a table with the intervals noted across the top, and the frequency of each below:
| 210-220 | 220-230 | 230-240 | 240-250 | 250-260 | 260-270 |
| 2 | 3 | 5 | 7 | 5 | 2 |
Example 3
| Interval: | 210-220 | 220-230 | 230-240 | 240-250 | 250-260 | 260-270 |
| Frequency: | 2 | 3 | 5 | 7 | 5 | 2 |
| Cumulative Frequency: | 224 8.33% | 524 20.83% | 1024 41.66% | 1724 70.83% | 2224 91.66% | 2424 100% |
Review
1. A weather forecaster highlights the lows over-night for the past 30 days in a small town in Wisconsin. The temperature readings are given in Fahrenheit, and are shown below. Use the data to complete the frequency table.
41∘,58∘,61∘,54∘,49∘,46∘,52∘,58∘,67∘,43∘,47∘,60∘,52∘,58∘,48∘,44∘,59∘,66∘,62∘,55∘,44∘,49∘,62∘,61∘,59∘,54∘,57∘,58∘,63∘,60∘
| Interval | Tally | Frequency |
| 40 - 44 | ||
| 45- 49 | ||
| 50 - 54 | ||
| 55 - 59 | ||
| 60 - 64 | ||
| 65 - 69 |
2. The following represents scores that a class received on their most recent Biology test. Complete the frequency table below.
58, 79, 81, 99, 68, 92, 76, 84, 53, 57, 81, 91, 77, 50, 65, 57, 51, 72, 84, 89
| Interval | Tally | Frequency |
| 50 - 59 | ||
| 60 - 69 | ||
| 70 - 79 | ||
| 80 - 89 | ||
| 90 - 99 |
3. James received the following scores on his quizzes in US History over the course of 1 year. Complete the frequency table below using the scores:
85, 72, 97, 81, 77, 93, 100, 75, 86, 70, 96, and 80.
| Interval/Grades | Tally | Frequency |
| 61 - 70 | ||
| 71 - 80 | ||
| 81 - 90 | ||
| 91 - 100 |
4. Sue competed against 14 others in a time trial for the 400-meter run at the state finals. Their times have been recorded in the table below. What percent of the runners completed the time trial between 50 and 53.9 seconds?
| Interval | Tally | Frequency |
| 50.0 - 50.9 | 0 | |
| 51.0 - 51.9 | || | 2 |
| 52.0 - 52.9 | 6 | |
| 53.0 - 53.9 | ||| | 3 |
| 54.0 - 54.9 | |||| | 4 |
5. The following data is the starting weights of 30 adults, in pounds, who participated in a study on weight loss. Use the data to create a cumulative frequency table. Determine appropriate intervals for the weights given.
195, 206, 100, 98, 150, 210, 195, 106, 195, 168, 180, 212, 104, 195, 100, 216, 195, 209, 112, 99, 206, 116, 195, 100, 142, 100, 135, 98, 160, 155
| Interval | Frequency | Cumulative Frequency |
6. The following table shows the weights in pounds for students attending a “Get Fit” summer program. Use the data to find cumulative frequency.
| Interval | Frequency | Cumulative Frequency |
| 91-100 | 6 | |
| 101-110 | 3 | |
| 111-120 | 0 | |
| 121-130 | 3 | |
| 131-140 | 0 | |
| 141-150 | 2 | |
| 151-160 | 2 |
7. 20 students were asked how many meals their family eats out in one week. The results are listed below. Complete the frequency table using this data.
{6, 5, 4, 5, 0, 7, 1, 5, 4, 4, 3, 2, 2, 3, 2, 4, 3, 4, 0, 7}
| Interval | Tally | Frequency | Cumulative Frequency |
| 0-1 | |||
| 2-3 | |||
| 4-5 | |||
| 6-7 |
8. The following graph shows the participants in Jane’s aerobics classes. How many total students does she teach on the given day?
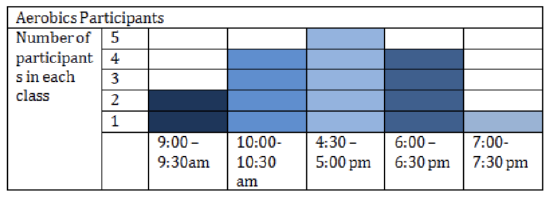
CC BY-NC-SA
9. The following table shows a cumulative frequency distribution of the ages of tri-athletes. According to the table, how many tri-athletes are in their forties?
| Age Group | Total |
| 20 - 29 | 8 |
| 20 - 39 | 18 |
| 20 - 49 | 25 |
| 20 - 59 | 31 |
| 20 - 69 | 35 |
10. The quiz scores for a job placement math assessment for the 10 applicants were: 61, 67, 81, 83, 87, 88, 89, 90, 98, and 100. Which frequency table is accurate for this set of data?
| Interval | Freq | Interval | Freq | Interval | Freq | Interval | Freq |
| 61 - 70 | 2 | 61 - 70 | 2 | 61 - 70 | 2 | 61 - 70 | 2 |
| 71 - 80 | 0 | 71 - 80 | 2 | 71 - 80 | 0 | 71 - 80 | 2 |
| 81 - 90 | 8 | 81 - 90 | 8 | 81 - 90 | 6 | 81 - 90 | 7 |
| 91 - 100 | 10 | 91 - 100 | 10 | 91 - 100 | 2 | 91 - 100 | 10 |
It is that time of year again. It is Easter, and it is time to hunt eggs. The kids have been divided up into age groups, and their eggs hidden in different areas of a large park. The adult leaders have gathered the data from the three age groups: “Kinders”, “Pee Wee”, and “Big Eggs”, and compiled the results into frequency tables. The problem is, each of the adult leaders reported their information differently.
For questions 11-13, use the data gathered by each adult leader and follow the instructions for interpreting the data given by each.
11. Team “Kinders” coach reported the following results for the number of eggs found by the kiddos in their group, convert them to a cumulative frequency chart.
| Time (s) in minutes | Frequency of Eggs Found |
| 0 - 5 | 20 |
| 5 - 10 | 35 |
| 10 - 15 | 15 |
| 15 - 20 | 22 |
| 20 - 25 | 8 |
| 25 - 30 | 9 |
12. Team “Pee Wee” also did a great job of finding eggs. Their results were recorded in a cumulative frequency table, convert to a frequency table.
| Time (s) in minutes | Cumulative Frequency of Eggs Found |
| 0 - 5 | 20 |
| 5 - 10 | 27 |
| 10 - 15 | 31 |
| 15 - 20 | 31 |
| 20 - 25 | 37 |
| 25 - 30 | 50 |
13. The “Big Eggs” were the champions the last three years running. They are known for always collecting the same amount of eggs in each interval. This year they collected a total of 120 eggs.
- Complete a frequency chart
- Complete a cumulative frequency chart
Vocabulary
| Term | Definition |
|---|---|
| cumulative frequency | Cumulative frequency is used to determine the number of observations that lie above (or below) a particular value in a data set. |
| cumulative frequency table | A cumulative frequency table shows how the cumulative frequency after each successive interval compares to the total frequency. |
| relative cumulative frequency | Relative cumulative frequency is a running total of relative frequencies of all values up to and including the current category. |
Additional Resources
Practice: Relative Frequency Interpretation
Real World: Burning Desire

