10.1: Linear Correlation and Regression

Linear Correlation Coefficient

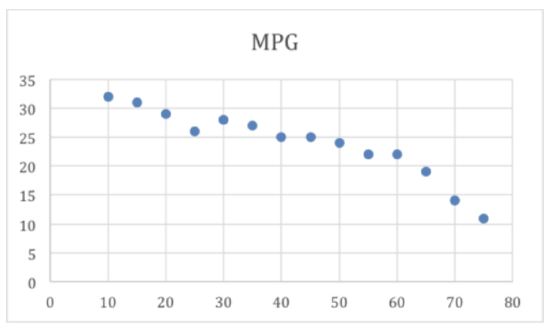
Suppose you have noted that your car seems to use more gas when you drive fast than when you drive more slowly. You decide to see how strong the relationship is, so you do some research, collect the data, and plot the data on the graph below, where the explanatory variable x is mph, and the response variable y is mpg. How can you describe how strong the correlation is without the graph?

Christian Haugen - https://www.flickr.com/photos/christianhaugen/3721602063 - CC BY-NC-SA

Linear Correlation Coefficient

The linear correlation coefficient (sometimes called Pearson’s Correlation Coefficient), commonly denoted r, is a measure of the strength of the linear relationship between two variables. The value of r has the following properties:

• r is always a value between -1 and +1
• The further an r value is from zero, the stronger the relationship between the two variables.
• The sign of r indicates the nature of the relationship: A positive r indicates a positive relationship, and a negative r indicates a negative relationship.

CC BY-NC-SA

Generally speaking, you may think of the values of r in the following manner:

• If |r| is between 0.85 and 1, there is a strong correlation.
• If |r| is between 0.5 and 0.85, there is a moderate correlation.
• If |r| is between 0.1 and 0.5, there is a weak correlation.
• If |r| is less than 0.1, there is no apparent correlation.

Naturally, r-value can be calculated, but the formula is a bit beyond the scope of this course. Fortunately, there are many excellent and free online calculators for determining the r-value of a set of data. In this lesson we will be using the one on Easy Calculations' website, but a search for “correlation calculator online” will yield the most current options.

At the risk of overloading you with new terms, there is one more that I think it is worth learning in this lesson, the coefficient of determination. The coefficient of determination is very simple to calculate if you know the correlation coefficient, since it is just r². The reason I mention it is that the coefficient of determination can be interpreted as the percentage of variation of the y variable that can be attributed to the relationship. In other words, a value of r²=.63 can be interpreted as “63% of the changes between one y value and another can be attributed to y’s relationship with x”.

Drawing Conclusions Given R-Values

1. Elaina is curious about the relationship between the weight of a dog and the amount of food it eats. Specifically, she wonders if heavier dogs eat more food, or if age and size factor in. She works at the Humane Society, and does some research. After some calculation, she determines that dog weight and food weight exhibit an r-value of 0.73.

Christian Haugen - https://www.flickr.com/photos/christianhaugen/3721602063

What can Elaina say about the relationship, based on her research? What percentage of the increases in food intake can she attribute to weight, according to her research?

The calculated r-value of 0.73 tells us that Elaina’s data demonstrates a moderate to strong correlation between the variables.

Since the coefficient of determination tells us the percentage of changes in the output variable that can be attributed to the input variable, we need to calculate r2:

r²=(0.73)²=.5329

Approximately 53% of increases in food intake can be attributed to the linear relationship between food intake and the weight of the dog, suggesting that other factors, perhaps age and size, are also involved.

2. Tuscany wonders if barrel racing times are related to the age of the horse. Specifically, she wonders if older horses take longer to complete a barrel racing run. As a member of the Pony Club, she does some research, and determines that horse age to barrel run time exhibits an r-value of 0.52.

What can Tuscany say about horse age vs barrel race time, according to her research?

Tuscany’s research suggests that there is a moderate to weak correlation between horse age and barrel run time. In other words, the research suggests that (0.52)²=.27=27% of the differences between barrel run times could be attributable to the linear relationship between barrel run time and the age of the horse.

Determining the Linear Correlation Coefficient of Determination

Sayber has collected the following data regarding player score vs age in his favorite online game. He suspects that increased age is not a good indicator of gaming ability. What are the linear correlation coefficient and coefficient of determination values of his data, and how do they support or not support Sayber’s hypothesis?

Age	Avg. Player Score
12	5,120
14	6,328
18	7,892
22	7,340
28	6,987
34	7,750
42	5,421

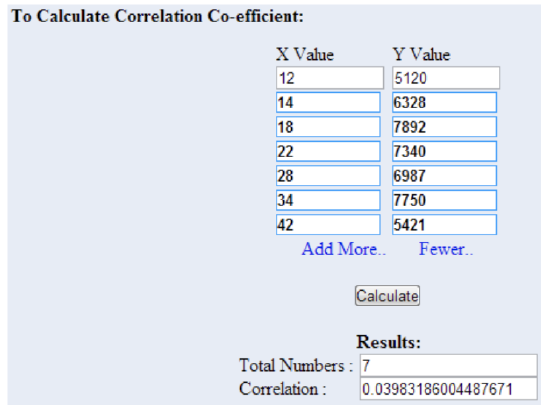
Let’s use the online calculator at Easy Calculation's website for this one.

I entered the explanatory (Age) and response (Player Score) values into the calculator:

Christian Haugen - https://www.flickr.com/photos/christianhaugen/3721602063 - CC BY-NC-SA

The linear correlation coefficient of approximately 0.04 suggests that there is no appreciable linear correlation. The coefficient of determination of 0.0016 suggests that perhaps 0.16% (practically none) of the variability of the player score is dependent on age.

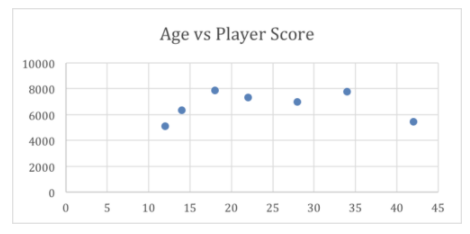
Looking at the scores, however, something seems a miss with our findings. The scores suggest that age has no bearing on player score, but look at the graph of the same data:

Christian Haugen - https://www.flickr.com/photos/christianhaugen/3721602063 - CC BY-NC-SA

The graph suggests that the youngest and oldest polled players score less than players in late teens to mid-thirties, which seems reasonable.

This is an important example of the weakness of using just one indicator of the relationship between two variables. As I noted early in the lesson, the r-value is only an indicator of linear correlation, it says nothing at all about other kinds of variable relationships. It is always a good idea to review your data in different ways to evaluate your initial conclusions.

Earlier Problem Revisited

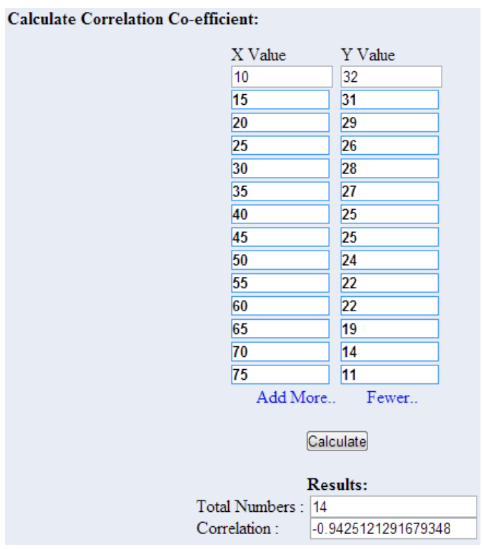
Suppose you have noted that your car seems to use more gas when you drive fast than when you drive more slowly. You decide to see how strong the relationship is, so you do some research, collect the data, and plot the data on the graph below, where the explanatory variable x is mph, and the response variable y is mpg. How can you describe how strong the correlation is without the graph?

Christian Haugen - https://www.flickr.com/photos/christianhaugen/3721602063 - CC BY-NC-SA

After the lesson above, we know that the r-value or r2-value of the relationship between MPG and MPH would describe the strength of the linear relationship in a single value.

By taking the data points detailed on the graph (in practice, of course, I would have had them in table format already, since I would have needed them to build the graph in the first place), and entering them into a free linear coefficient calculator online, I get an r-value of -.943, indicating a strong negative relationship. This also translates into an r²-value of (−0.943)2=0.89, indicating that the research suggests that approximately 89% of the decrease in MPG from left to right across the graph can be attributed to the increase in MPH.

---

Examples

Example 1

What can you say about the strength of a linear relationship with a r-value of -0.87

An |r| of > 0.85 indicates a strong linear relationship. The fact that r is negative indicates that as x increases, y decreases.

Example 2

What can you say about the level of negative correlation of a relationship if you know the coefficient of determination is 0.82?

Nothing! The coefficient of determination is r2, and therefore always positive. We know that |r|=.82^.5≈.91, so this is a strong linear correlation, but we have no idea if it is positive or negative.

Example 3

How much of the variability of y is attributable to x in a relationship with an r-value of 0.76?

The coefficient of determination describes the variation in y attributable to x, so we need to find r²:(0.76)²=.5776. Approximately 57.76% of the change in y-values can be attributed to the change in x.

---

Review

For questions 1-5, describe the relationship based on the r-value.

1. r=0

2. r=0.91

3. r=−0.49

4. r=0.05

5. r=1

For questions 6-10, describe the relationship based on the coefficient of determination:

6. r²=0.82

7. r²=0.15

8. r²=0.47

9. r²=1

10. r²=0

Questions 11-15 refer to the data in the following table:

X	Y
5	70
7	69
13	58
22	47
36	36
38	25
45	14

11. What is the linear correlation coefficient of the data?

12. What does r tell you about the relationship?

13. What is the r² value of the data?

14. What does the coefficient of determination tell you about this relationship?

15. What would a graph of the data look like?

---

Review (Answers)

To view the Review answers, open this PDF file and look for section 11.2.

---

Vocabulary

Term	Definition
bivariate data	Bivariate data consists of two paired sets of data.
correlation coefficient	The correlation coefficient is a standard quantitative measure of best fit of a line. It has the symbol r and has values from -1 to +1.
deterministic	A deterministic relationship indicates that the value of one variable can be reliably and accurately determined by the manipulation of the other variable.
explanatory variables	Explanatory variables are another name for independent variables.
linear correlation	Linear correlation is a measure of the strength of the linear relationship between two random variables.
linear correlation coefficient	A linear correlation coefficient or r -value of a relationship between two variables describes the strength of the linear relationship.
response variables	Response variables are another name for dependent variables.
scatter plot	A scatter plot is a plot of the dependent variable versus the independent variable and is used to investigate whether or not there is a relationship or connection between 2 sets of data.
Scatterplot	A scatterplot is a type of visual display that shows pairs of data for two different variables.
Slope	Slope is a measure of the steepness of a line. A line can have positive, negative, zero (horizontal), or undefined (vertical) slope. The slope of a line can be found by calculating “rise over run” or “the change in the y over the change in the x.” The symbol for slope is m
Slope-Intercept Form	The slope-intercept form of a line is y=mx+b, where m is the slope and b is the y−intercept.

---

Additional Resources

PLIX: Play, Learn, Interact, eXplore - Regression and Correlation

Real World: At the Height of Your Career