1.10: 45-45-90 Right Triangles
- Page ID
- 14088
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Leg times \(\sqrt{2}\) equals hypotenuse.
45-45-90 Right Triangles
A right triangle with congruent legs and acute angles is an Isosceles Right Triangle. This triangle is also called a 45-45-90 triangle (named after the angle measures).
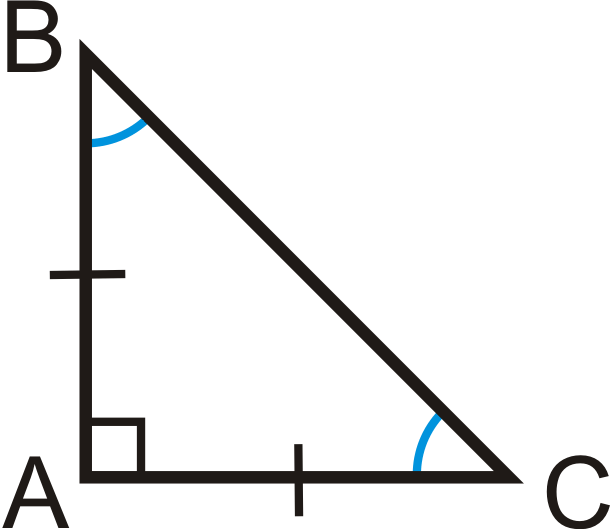
\(\Delta ABC\) is a right triangle with \(m\angle A=90^{\circ}\), \(\overline{AB} \cong \overline{AC}\) and \(m\angle B=m\angle C=45^{\circ}\).
45-45-90 Theorem: If a right triangle is isosceles, then its sides are in the ratio \(x:x:x\sqrt{2}\). For any isosceles right triangle, the legs are \(x\) and the hypotenuse is always \(x\sqrt{2}\).
What if you were given an isosceles right triangle and the length of one of its sides? How could you figure out the lengths of its other sides?
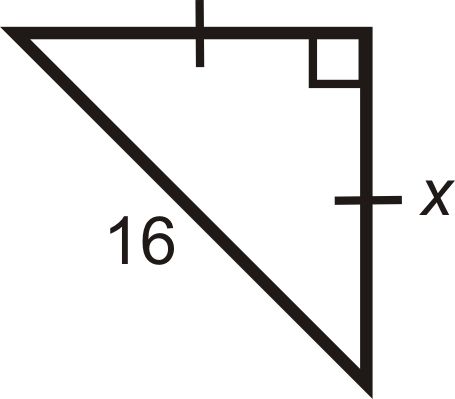
Find the length of \(x\).
Solution
Use the \(x:x:x\sqrt{2}\) ratio.
Here, we are given the hypotenuse. Solve for \(x\) in the ratio.
\(\begin{aligned} x\sqrt{2} =16\\ x=16\sqrt{2}\cdot \dfrac{\sqrt{2}}{\sqrt{2}}=\dfrac{16\sqrt{2}}{2}=8\sqrt{2} \end{aligned}\)
Find the length of \(x\), where \(x\) is the hypotenuse of a 45-45-90 triangle with leg lengths of \(5\sqrt{3}\).
Solution
Use the \(x:x:x\sqrt{2}\) ratio.
\(x=5\sqrt{3}\cdot\sqrt{2}=5\sqrt{6}\)
Find the length of the missing side.
Solution
Use the \(x:x:x\sqrt{2}\) ratio. \(TV=6\) because it is equal to \(ST\). So, \(SV=6 \cdot \sqrt{2}=6\sqrt{2}\).
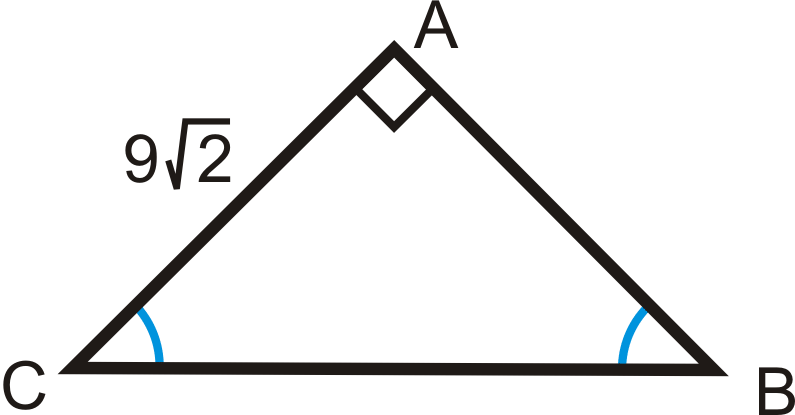
Find the length of the missing side.
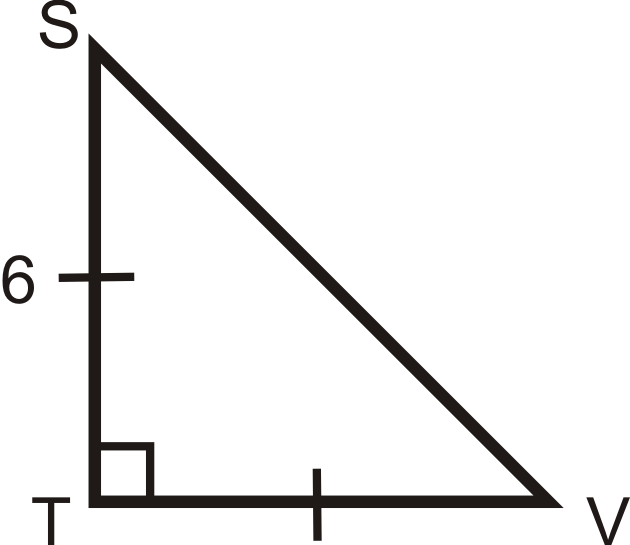
Solution
Use the \(x:x:x\sqrt{2}\) ratio. \(AB=9\sqrt{2}\) because it is equal to \(AC\). So, \(BC=9\sqrt{2}\cdot\sqrt{2}=9\cdot 2=18\).
A square has a diagonal with length 10, what are the lengths of the sides?
Solution
Draw a picture.
We know half of a square is a 45-45-90 triangle, so \(10=s\sqrt{2}\).
\(\begin{aligned} s\sqrt{2}&=10 \\ s&=10\sqrt{2}\cdot \dfrac{\sqrt{2}}{\sqrt{2}}=\dfrac{10\sqrt{2}}{2}=5\sqrt{2} \end{aligned}\)
Review
- In an isosceles right triangle, if a leg is 4, then the hypotenuse is __________.
- In an isosceles right triangle, if a leg is x, then the hypotenuse is __________.
- A square has sides of length 15. What is the length of the diagonal?
- A square’s diagonal is 22. What is the length of each side?
For questions 5-11, find the lengths of the missing sides. Simplify all radicals.
-
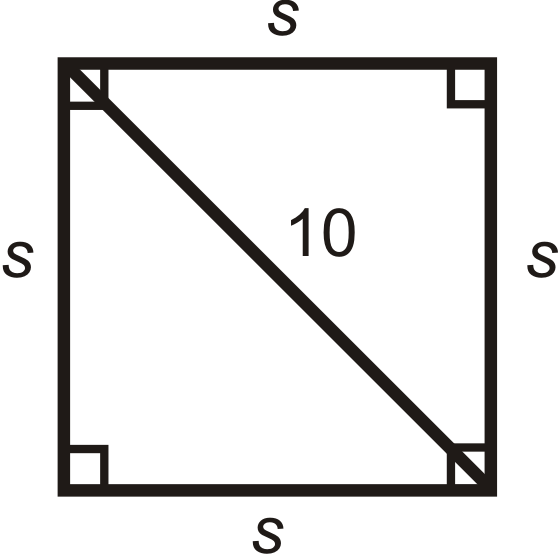
Figure \(\PageIndex{5}\) -
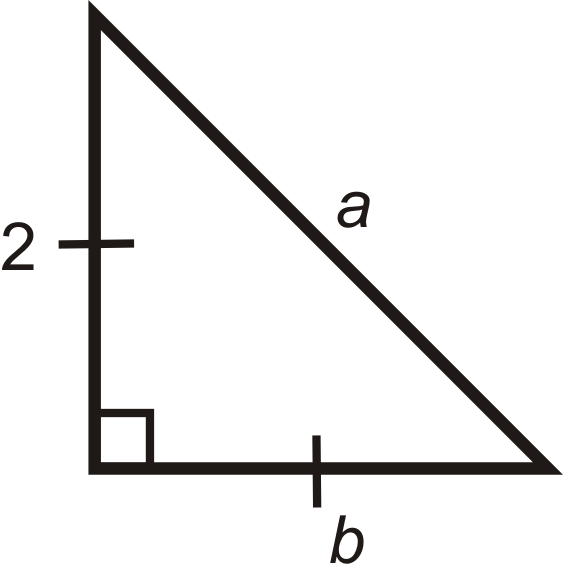
Figure \(\PageIndex{6}\) -
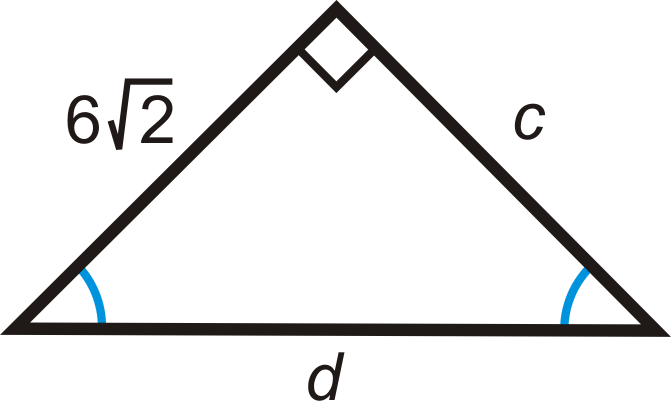
Figure \(\PageIndex{7}\) -
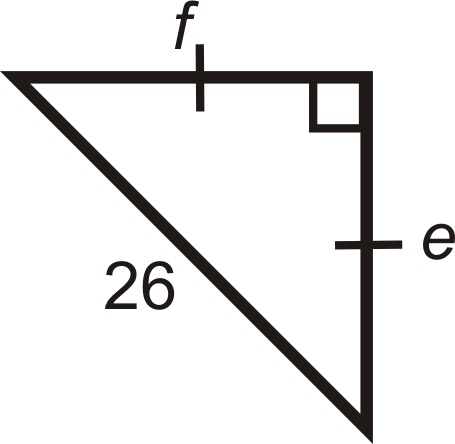
Figure \(\PageIndex{8}\) -
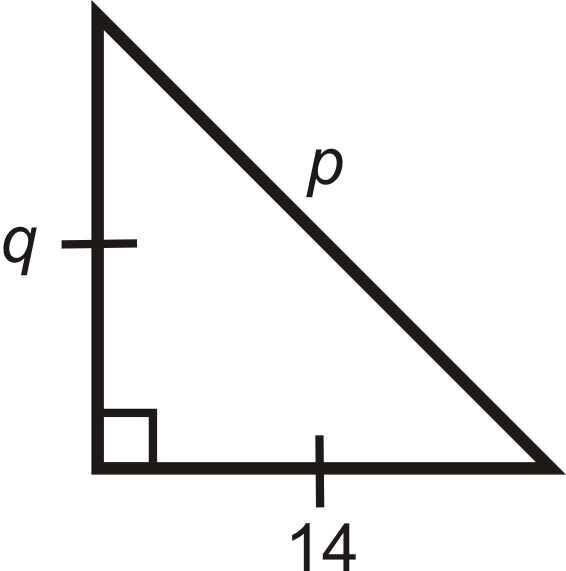
Figure \(\PageIndex{9}\) -
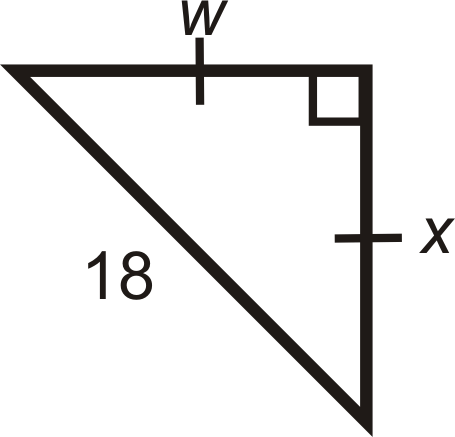
Figure \(\PageIndex{10}\) -
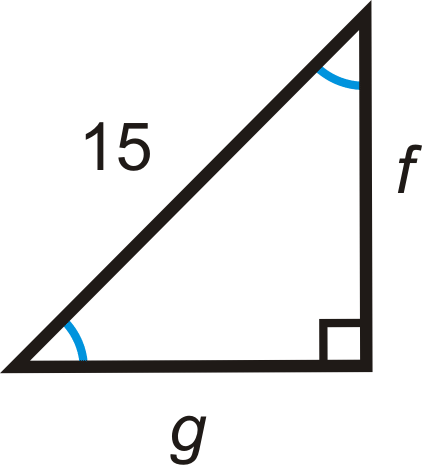
Figure \(\PageIndex{11}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 8.5.
Resources
Vocabulary
| Term | Definition |
|---|---|
| 45-45-90 Theorem | For any isosceles right triangle, if the legs are x units long, the hypotenuse is always \(x\sqrt{2}\). |
| 45-45-90 Triangle | A 45-45-90 triangle is a special right triangle with angles of \(45^{\circ}\), \(45^{\circ}\), and \(90^{\circ}\). |
| Hypotenuse | The hypotenuse of a right triangle is the longest side of the right triangle. It is across from the right angle. |
| Legs of a Right Triangle | The legs of a right triangle are the two shorter sides of the right triangle. Legs are adjacent to the right angle. |
| Radical | The √, or square root, sign. |
Additional Resources
Video: Solving Special Right Triangles
Activities: 45-45-90 Right Triangles Discussion Questions
Study Aids: Special Right Triangles Study Guide
Practice: 45-45-90 Right Triangles
Real World: Fighting the War on Drugs Using Geometry and Special Triangles

