2.2.4: Solve Right Triangles
- Page ID
- 14341
Using the inverse trigonometric functions to solve for missing information about right triangles.
Inverse Trigonometric Ratios
In mathematics, the word inverse means “undo.” For example, addition and subtraction are inverses of each other because one undoes the other. When we use the inverse trigonometric ratios, we can find acute angle measures as long as we are given two sides.
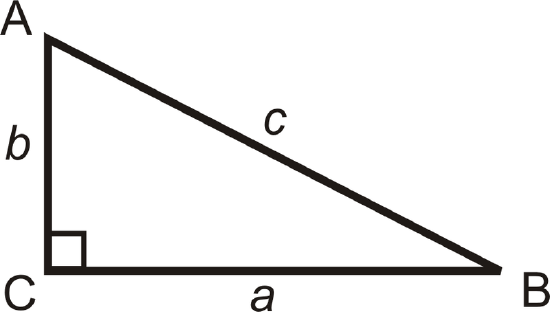
Inverse Tangent: Labeled \(\tan ^{-1}\), the “-1” means inverse.
\(\tan ^{-1} \left(\dfrac{b}{a}\right)=m\angle B\) and \(\tan ^{-1} \left(\dfrac{a}{b}\right)=m\angle A.\)
Inverse Sine: Labeled \(\sin ^{-1}\).
\(\sin ^{-1} \left(\dfrac{b}{c}\right)=m\angle B\) and \(\sin ^{-1} \left(\dfrac{a}{c}\right)=m\angle A.\)
Inverse Cosine: Labeled \(\cos ^{-1}\).
\(\cos ^{-1} \left(\dfrac{a}{c}\right)=m\angle B\) and \(\cos ^{-1} \left(\dfrac{b}{c}\right)=m\angle A.\)
In most problems, to find the measure of the angles you will need to use your calculator. On most scientific and graphing calculators, the buttons look like \([\sin ^{-1}]\), \([\cos ^{-1}]\), and \([\(\tan ^{-1}]\). You might also have to hit a shift or 2nd button to access these functions.
Now that you know both the trig ratios and the inverse trig ratios you can solve a right triangle. To solve a right triangle, you need to find all sides and angles in it. You will usually use sine, cosine, or tangent; inverse sine, inverse cosine, or inverse tangent; or the Pythagorean Theorem.
What if you were told the tangent of \(\angle Z\) is 0.6494? How could you find the measure of \(\angle Z\)?
Solve the right triangle.
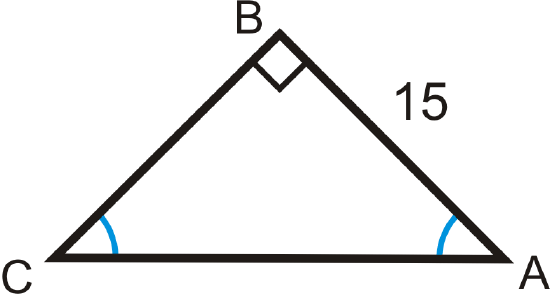
Solution
The two acute angles are congruent, making them both \(45^{\circ}\). This is a 45-45-90 triangle. You can use the trigonometric ratios or the special right triangle ratios.
Trigonometric Ratios
\(\begin{array}{rlrl}
\tan 45^{\circ} & =\dfrac{15}{B C} & \sin 45^{\circ} & =\dfrac{15}{A C} \\
B C & =\dfrac{15}{\tan 45^{\circ}}=15 & A C & =\dfrac{15}{\sin 45^{\circ}} \approx 21.21
\end{array}\)
45-45-90 Triangle Ratios
\(BC=AB=15 \text{, } AC=15\sqrt{2} \approx 21.21\)
Use the sides of the triangle and your calculator to find the value of \(\angle A\). Round your answer to the nearest tenth of a degree.
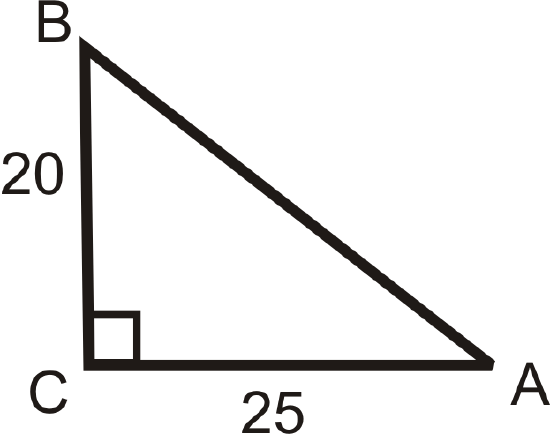
Solution
In reference to \(\angle A\), we are given the opposite leg and the adjacent leg. This means we should use the tangent ratio.
\(\tan A=\dfrac{20}{25}=\dfrac{4}{5}\). So, \(\tan ^{-1} \dfrac{4}{5}=m\angle A\). Now, use your calculator.
If you are using a TI-83 or 84, the keystrokes would be: [2nd][TAN](\(\dfrac{4}{5}\)) [ENTER] and the screen looks like:

\(m\angle A \approx 38.7^{\circ}\)
\(\angle A\) is an acute angle in a right triangle. Find \(m\angle A\) to the nearest tenth of a degree for \(\sin A=0.68\), \(\cos A=0.85\), and \(\tan A=0.34\).
Solution
\(\begin{aligned} m\angle A&=\sin ^{-1} 0.68\approx 42.8^{\circ} \\ m\angle A&=\cos ^{-1} 0.85\approx 31.8^{\circ} \\ m\angle A&=\tan ^{-1} 0.34\approx 18.8^{\circ} \end{aligned}\)
Solve the right triangle.
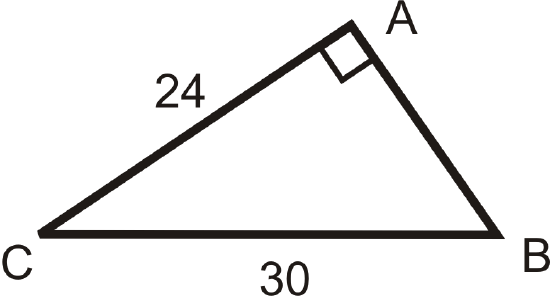
Solution
To solve this right triangle, we need to find \(AB\), \(m\angle C\) and \(m\angle B\). Use only the values you are given.
\(\underline{AB}: \text{ Use the Pythagorean Theorem.}\)
\(\begin{aligned} 24^2+AB^2&=30^2 \\ 576+AB^2&=900 \\ AB^2&=324 \\ AB&=\sqrt{324}=18 \end{aligned}\)
\(\underline{m\angle B} : \text{ Use the inverse sine ratio.}\)
\(\begin{aligned} \sin B &=\dfrac{24}{30}=\dfrac{4}{5} \\ \sin ^{-1} (45) &\approx 53.1^{\circ} =m\angle B\end{aligned}\)
\(\underline{m\angle C} : \text{ Use the inverse cosine ratio.}\)
\(\cos C=\dfrac{24}{30}=\dfrac{4}{5} \rightarrow \cos ^{-1} (\dfrac{4}{5})\approx 36.9^{\circ} =m\angle C\)
When would you use sin and when would you use \(\sin ^{-1}\) ?
Solution
You would use sin when you are given an angle and you are solving for a missing side. You would use \(\sin ^{-1} \)when you are given sides and you are solving for a missing angle.
Review
Use your calculator to find \(m\angle A\) to the nearest tenth of a degree.
-
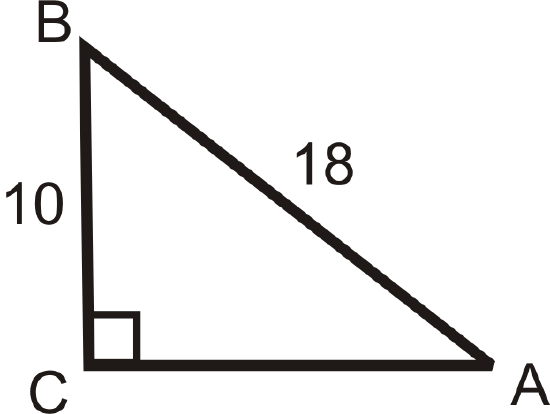
Figure \(\PageIndex{6}\) -
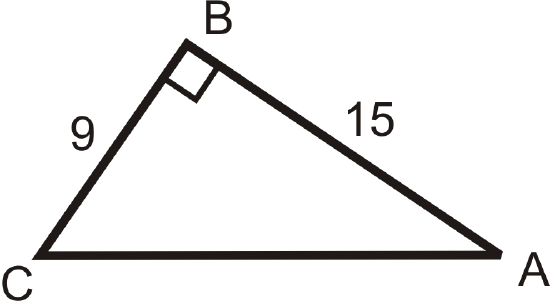
Figure \(\PageIndex{7}\) -
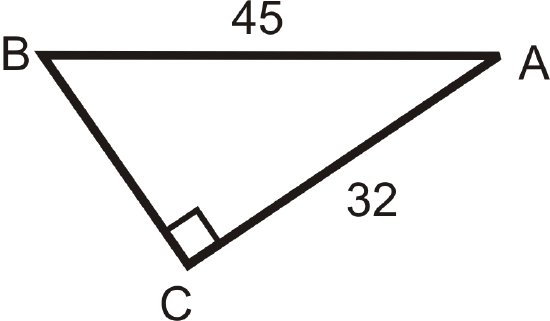
Figure \(\PageIndex{8}\) -
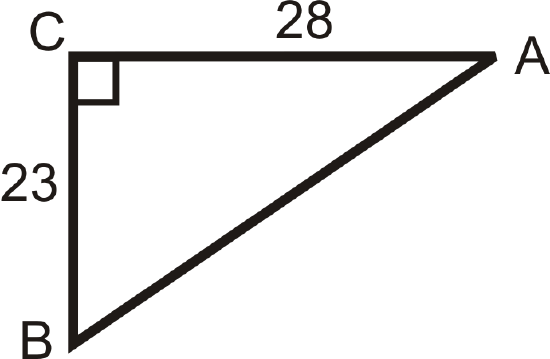
Figure \(\PageIndex{9}\) -
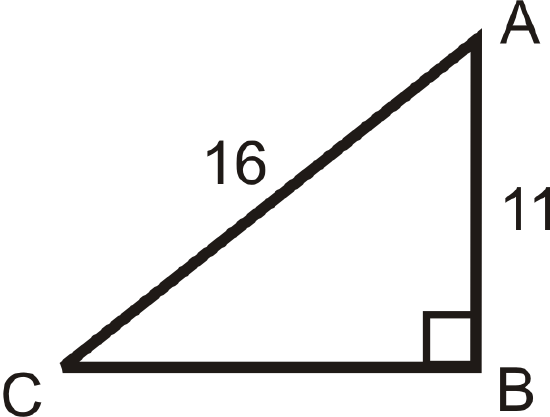
Figure \(\PageIndex{10}\) -
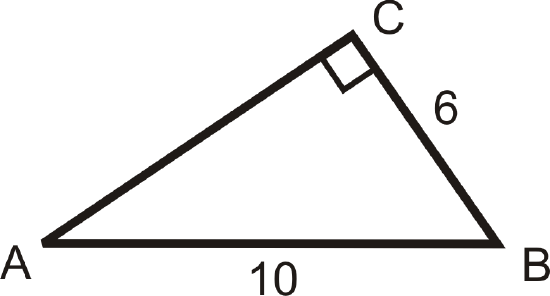
Figure \(\PageIndex{11}\)
Let \(\angle A\) be an acute angle in a right triangle. Find \(m\angle A\) to the nearest tenth of a degree.
- \(\sin A=0.5684\)
- \(\cos A=0.1234\)
- \(\tan A=2.78\)
- \(\cos ^{-1} 0.9845\)
- \(\tan ^{-1} 15.93\)
- \(\sin ^{-1} 0.7851\)
Solving the following right triangles. Find all missing sides and angles. Round any decimal answers to the nearest tenth.
-
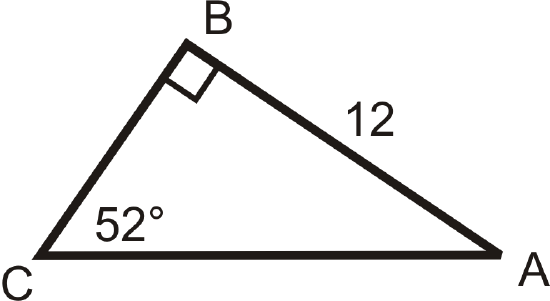
Figure \(\PageIndex{12}\) -
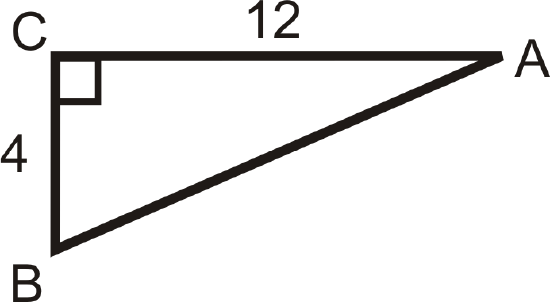
Figure \(\PageIndex{13}\) -
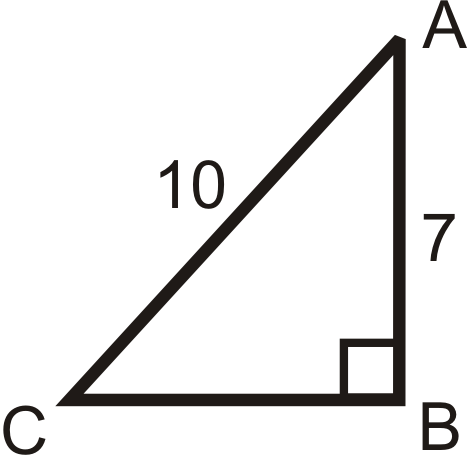
Figure \(\PageIndex{14}\) -
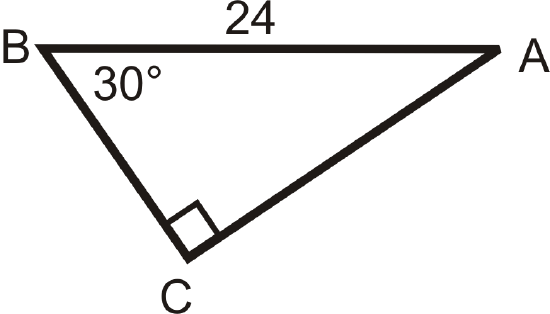
Figure \(\PageIndex{15}\) -
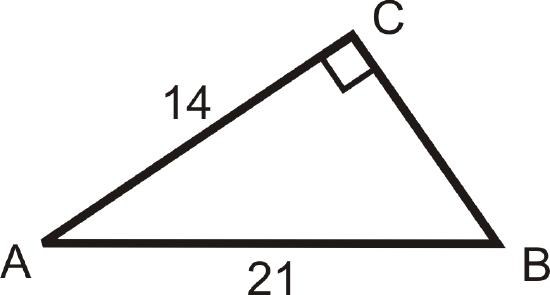
Figure \(\PageIndex{16}\) -
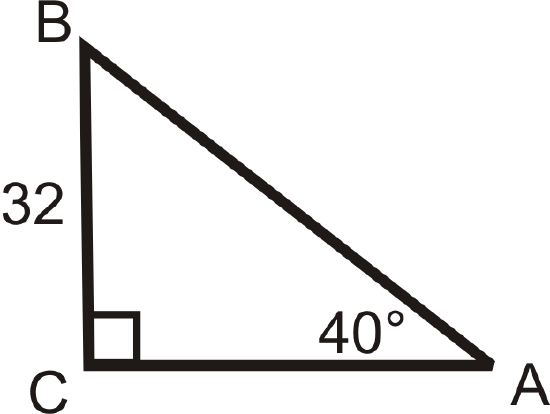
Figure \(\PageIndex{17}\) -
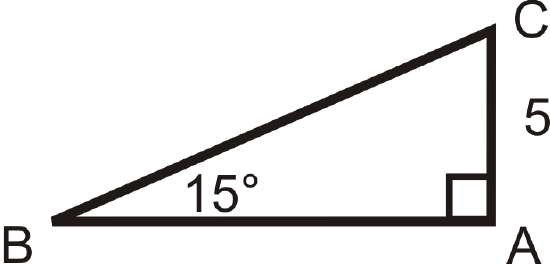
Figure \(\PageIndex{18}\) -
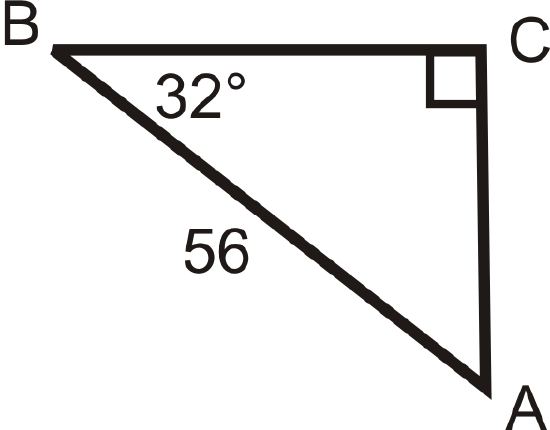
Figure \(\PageIndex{19}\) -
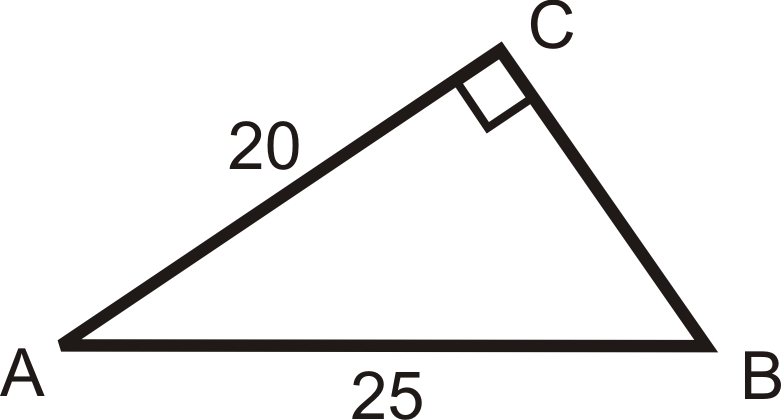
Figure \(\PageIndex{20}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 8.10.
Additional Resources
Video: Introduction to Inverse Trigonometric Functions
Activities: Inverse Trigonometric Ratios Discussion Questions
Study Aids: Trigonometric Ratios Study Guide
Practice: Solve Right Triangles

