2.2.3: Right Triangles and Bearings
- Page ID
- 14340
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Directions based off compass points.
While on a camping trip with your friends, you take an orienteering trip. You end up on a course which results in you hiking \(30^{\circ}\) west of due south. This is represented as \(S30^{\circ}W\) (always start with N or S, then the number of degrees to the east or west of there). You hike until you are 5 miles from where you started. Is it possible to determine how far west you are from where you started?
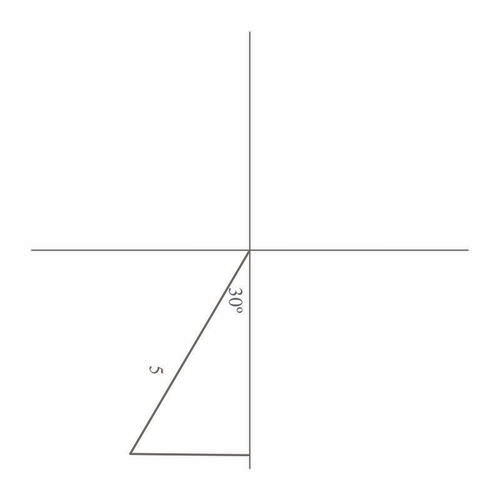
Bearings
You can use right triangles to find distances using angles given as bearings. In navigation, a bearing is the direction from one object to another. In air navigation, bearings are given as angles rotated clockwise from the north.
The graph below shows an angle of 70 degrees:
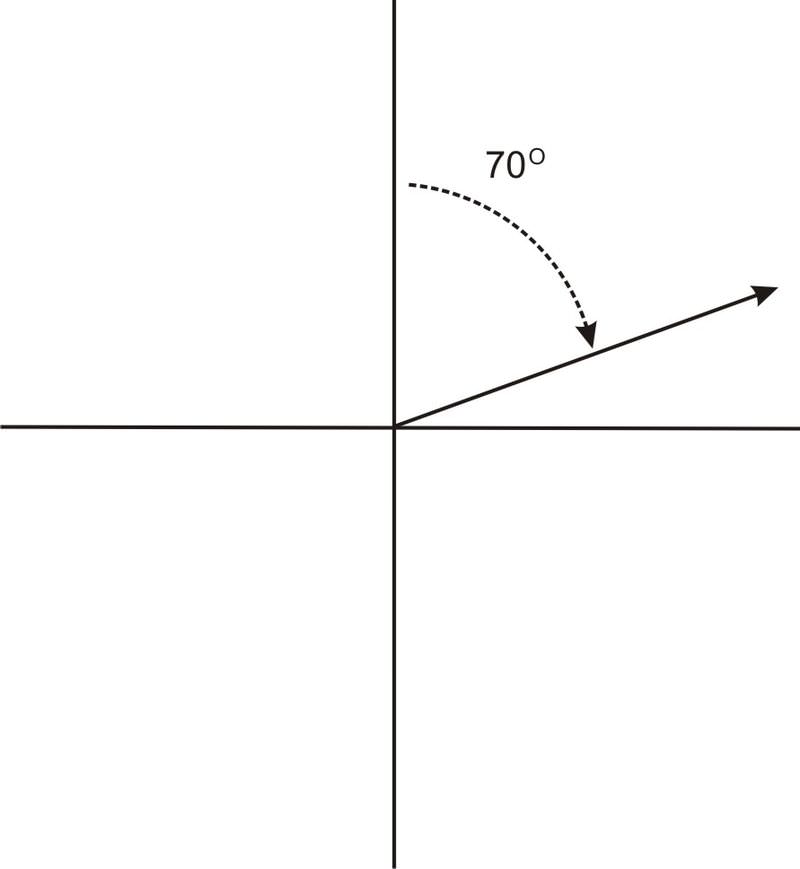
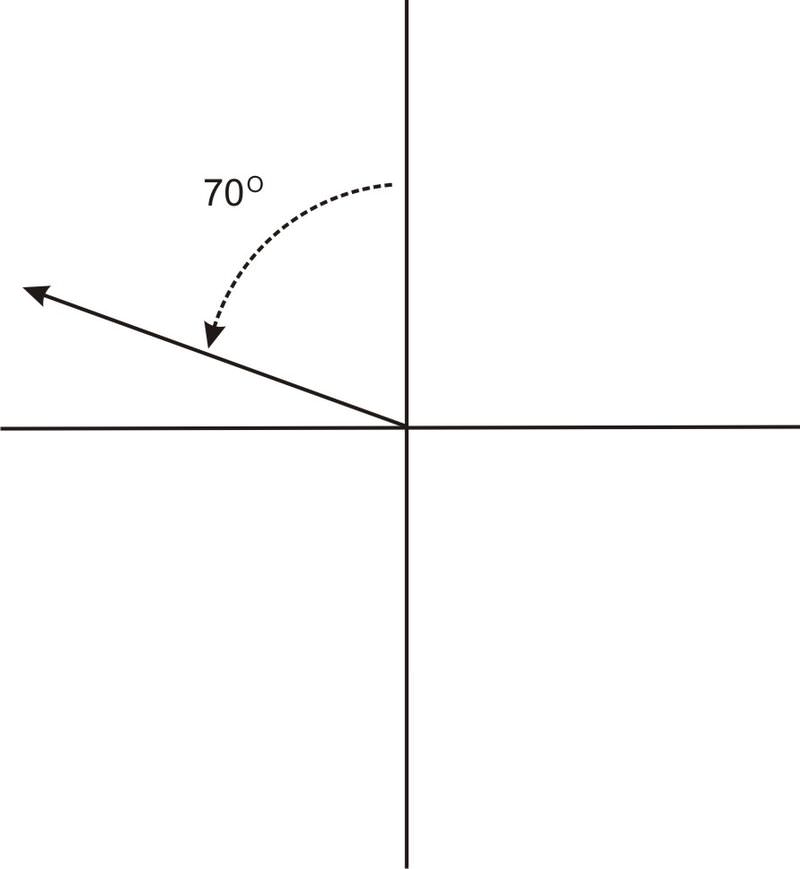
It is important to keep in mind that angles in navigation problems are measured this way, and not the same way angles are otherwise measured in trigonometry. Further, angles in navigation and surveying may also be given in terms of north, east, south, and west. For example, \(N70^{\circ}E\) refers to an angle 70 degrees to the east of straight north, while \(N70^{\circ}W\) refers to an angle 70 degrees west of straight north. \(N70^{\circ}E\) is the same as the angle shown in the graph above. \(N70^{\circ}W\) would result in an angle in the second quadrant, like this:
Now, let's look at a problem where we find the distance using right triangles as bearings.
A ship travels on a \(N50^{\circ}E\) course. The ship travels until it is due north of a port which is 10 nautical miles due east of the port from which the ship originated. How far did the ship travel?
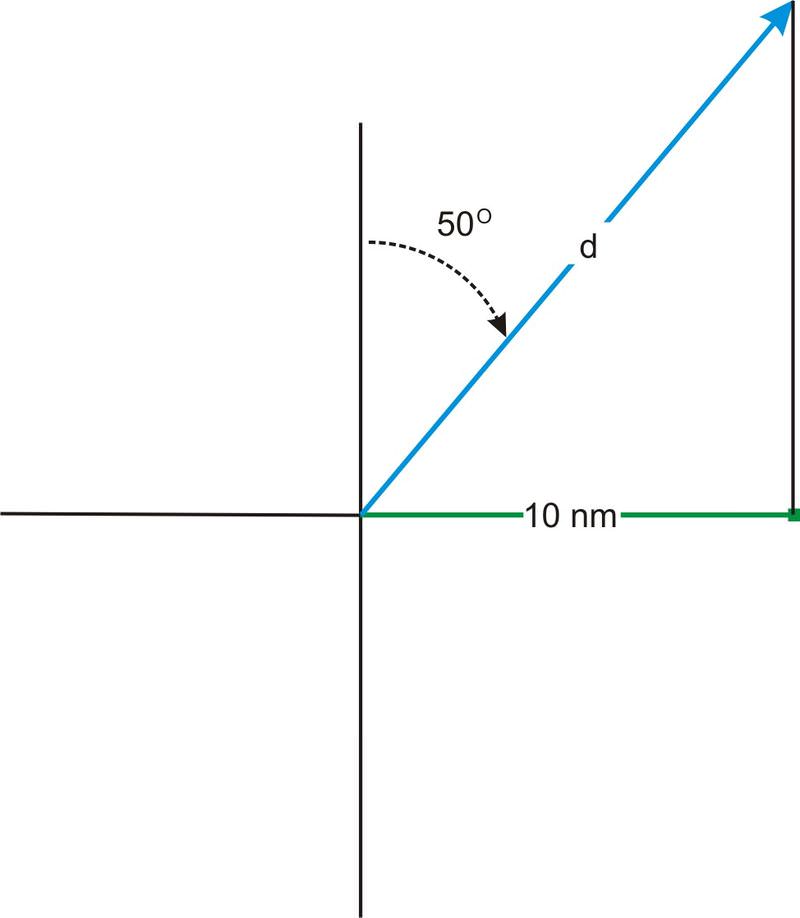
The angle between d and 10 nm is the complement of \(50^{\circ}\), which is \(40^{\circ}\). Therefore we can find d using the cosine function:
\(\begin{aligned} \cos 40^{\circ}&=\dfrac{\text{adjacent}}{\text{hypotenuse}}=\dfrac{10}{d} \\ \cos 40^{\circ}&=\dfrac{10}{d} \\ d \cos 40^{\circ}&=10 \\ d&=10 \cos 40^{\circ}\approx 13.05 \text{ nautical miles}\end{aligned}\)
An airplane flies on a course of \(S30^{\circ}E\), for 150 km. How far south is the plane from where it originated?
Construct a triangle using the known information, and then use the cosine function to solve the problem:
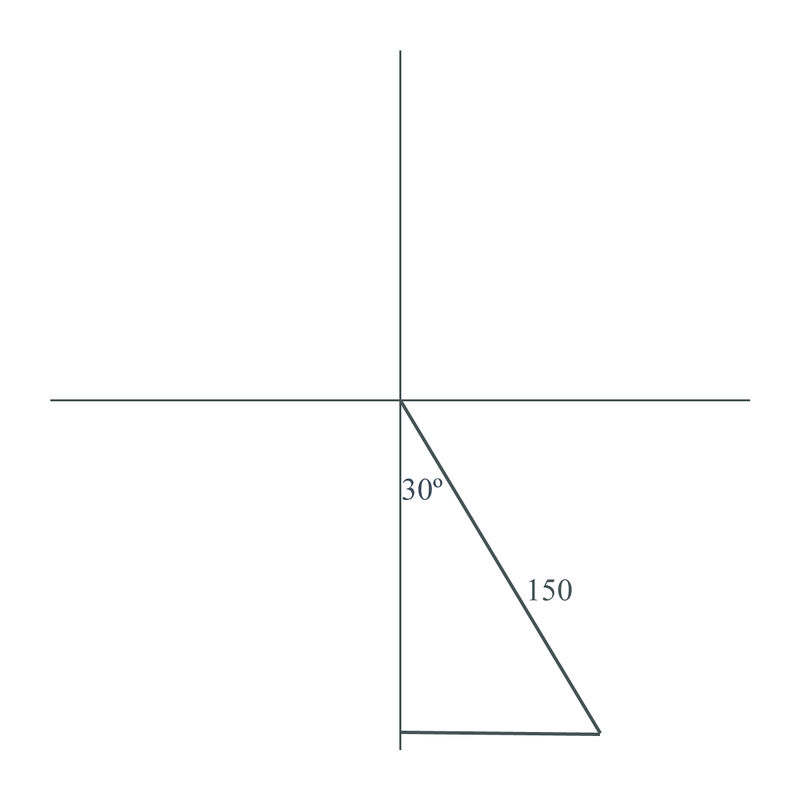
\(\begin{aligned} \cos 30^{\circ} &= \dfrac{\text{adjacent}}{\text{hypotenuse}}=\dfrac{y}{150} \\ \cos 30^{\circ} &=\dfrac{y}{150} \\ 150\cos 30^{\circ}&=y \\ y&=150 \cos 30^{\circ}\approx 130 \text{ km}\end{aligned}\)
Jean travels to school each day by walking 200 meters due north, and then turning right and walking 100 meters due eEast. If she had walked in a straight line, what would the angle between her home and the school be if the beginning of the angle is taken from due north? What would be two different ways to describe the direction to take walking there in a straight line, u\sin g what we've learned in this section?
From the triangle given above, we can use the tangent function to determine the angle if she had walked in a straight line.
\(\begin{aligned} \tan\theta &=\dfrac{\text{opposite}}{\text{adjacent}}= \dfrac{100}{200} \\ \tan\theta &=\dfrac{100}{200} \\ \theta &=26.57^{\circ} \end{aligned}\)
One way of describing her straight line path is how far east of north she is: \(N26.57^{\circ}E\)
Also, since we know the bearings are usually based off of north, her motion can be described as simply a bearing of \(26.57^{\circ}\).
Earlier, you were given some information about a hiking trip, and asked "Is it possible to determine how far south you are from where you started?"
Solution
The story specified that you hiked for 5 miles from your starting point, on a bearing of \(S30^{\circ}W\). Applying this data with your understanding of how to construct a triangle using bearings, you can draw the following:
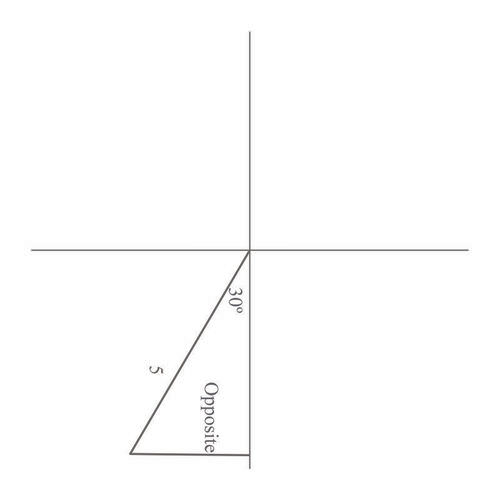
This shows that the opposite side of the triangle is what's not known. Therefore, you can use the \sin e function to solve the problem:
\(\begin{aligned} \sin 30^{\circ}&= \dfrac{\text{opposite}}{5} \\ \text{opposite }&= 5\sin 30^{\circ} \\ \text{opposite}&=(5)(.5)=2.5 \end{aligned}\)
You are 2.5 miles west of where you started.
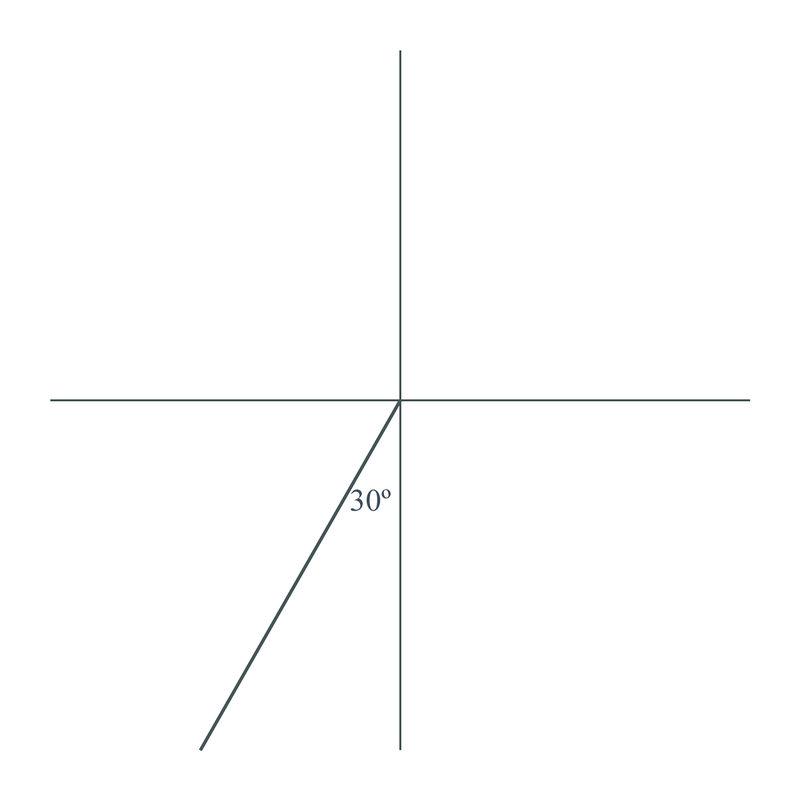
Plot a course or bearing of \(240^{\circ}\) on a rectangular coordinate system.
Solution
This is the same as \(S30^{\circ}W\) (recall that due south is 270 degrees, so 240 degrees is 30 degrees west of that) and can be plotted as:
Scott is boating on a course of \(N15^{\circ}E\). What course would he need to take to return to where he came from?
Solution
The opposite direction would return him to his starting point. This would be \(S15^{\circ}W\).
Adam hikes on a course of \(N 47^{\circ}E\) for 7 km. How far east is Adam from where he started?
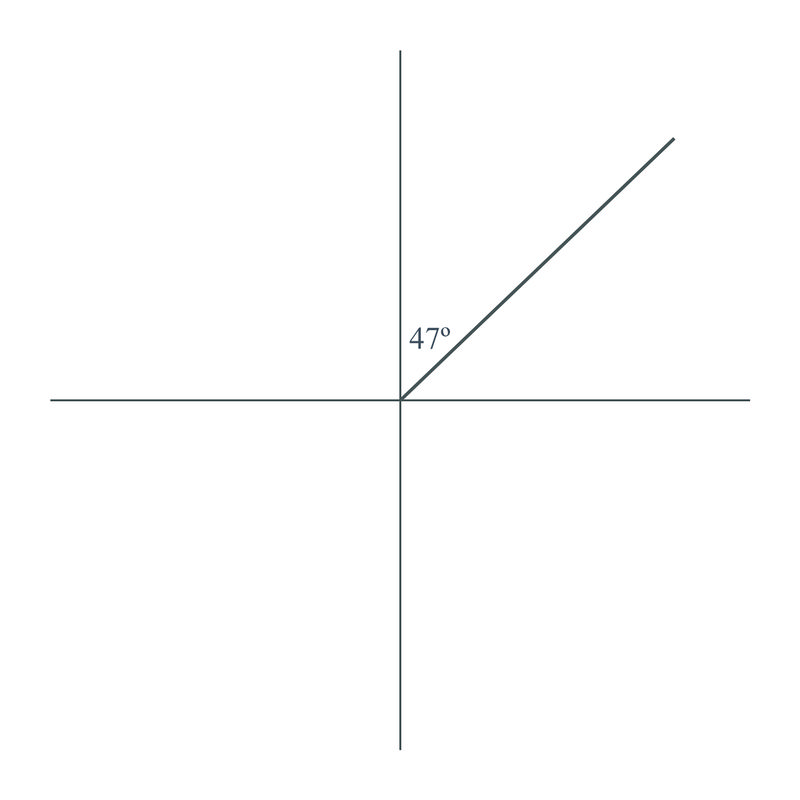
Solution
Find the length of the triangle above (which is how far Adam traveled east) by u\sin g the \sin e function:
\(\begin{aligned} \sin 47^{\circ}&=\dfrac{x}{7} \\ x&=7\sin 47^{\circ} \\ x&=(7)(.7313) \\ x&=5.1191 \end{aligned}\)
He is 5.1191 km east of where he started.
Review
- Plot a course of \(N40^{\circ}E\) on a rectangular coordinate system.
- Plot a course of \(60^{\circ}\) on a rectangular coordinate system.
- Plot a course of \(S70^{\circ}W\) on a rectangular coordinate system.
- Plot a course of \(S5^{\circ}W\) on a rectangular coordinate system.
- Plot a course of \(N42^{\circ}W\) on a rectangular coordinate system.
- You are on a course of \(N55^{\circ}E\). What course would you need to take to return to where you came from?
- You are on a course of \(S34^{\circ}W\). What course would you need to take to return to where you came from?
- You are on a course of \(N72^{\circ}W\). What course would you need to take to return to where you came from?
- You are on a course of \(S10^{\circ}E\). What course would you need to take to return to where you came from?
- You are on a course of \(N25^{\circ}W\). What course would you need to take to return to where you came from?
- You are on a course of \(47^{\circ}\) for 5 km. How far east are you from where you started?
- You are on a course of \(S32^{\circ}E\) for 8 km. How far east are you from where you started?
- You are on a course of \(N15^{\circ}W\) for 10 km. How far west are you from where you started?
- You are on a course of \(S3^{\circ}W\) for 12 km. How far west are you from where you started?
- You are on a course of \(S67^{\circ}E\) for 6 km. How far east are you from where you started?
Review (Answers)
To see the Review answers, open this PDF file and look for section 1.14.
Vocabulary
| Term | Definition |
|---|---|
| Bearing | Bearing is how direction is measured at sea. North is \(0^{\circ}\), east is \(90^{\circ}\), south is \(180^{\circ}\), and west is \(270^{\circ}\). |
Additional Resources
Video: Right Triangle Models - Example 1
Practice: Right Triangles and Bearings

