2.2.5: Applications of Inverse Trigonometric Functions
- Page ID
- 14342
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Angle values in real world examples.
You are mapping out a hiking trip to a new spot in the state park near your home. On your map, you know that you are supposed to go on a course which ends with you having moved 2.5 miles East and 3 miles South. Your map, with the start and end points, is shown here:

Now you need to calculate the angle that you need to walk with respect to due East. Can you find a way to calculate this angle using inverse trig functions?
Applying Inverse Trig Functions
The following problems are real-world problems that can be solved using the trigonometric functions. In everyday life, indirect measurement is used to obtain answers to problems that are impossible to solve using measurement tools. However, mathematics will come to the rescue in the form of trigonometry to calculate these unknown measurements.
On a cold winter day the sun streams through your living room window and causes a warm, toasty atmosphere. This is due to the angle of inclination of the sun which directly affects the heating and the cooling of buildings. Noon is when the sun is at its maximum height in the sky and at this time, the angle is greater in the summer than in the winter. Because of this, buildings are constructed such that the overhang of the roof can act as an awning to shade the windows for cooling in the summer and yet allow the sun’s rays to provide heat in the winter. In addition to the construction of the building, the angle of inclination of the sun varies according to the latitude of the building’s location.
If the latitude of the location is known, then the following formula can be used to calculate the angle of inclination of the sun on any given date of the year:
\(\text{Angle of sun}=90^{\circ}−\text{latitude}+−23.5^{\circ}\cdot \cos\left[(N+10)\dfrac{360}{365}\right]\) where \(N\) represents the number of the day of the year that corresponds to the date of the year. Note: This formula is accurate to \(\pm \dfrac{1^{\circ}}{2}\)
Determine the measurement of the sun’s angle of inclination for a building located at a latitude of \(42^{\circ}\), March \(10^{th}, the \(69^{th}\) day of the year.
\(\begin{array}{l}
\text { Angle of sun }=90^{\circ}-42^{\circ}+-23.5^{\circ} \cdot \cos \left[(69+10) \dfrac{360}{365}\right] \\
\text { Angle of sun }=48^{\circ}+-23.5^{\circ}(0.2093) \\
\text { Angle of sun }=48^{\circ}-4.92^{\circ} \\
\text { Angle of } \operatorname{sun}=43.08^{\circ}
\end{array}\)
Determine the measurement of the sun’s angle of inclination for a building located at a latitude of \(20^{\circ}\), September \(21^{st}\).
\(\begin{array}{l}
\text { Angle of sun}=90^{\circ}-20^{\circ}+-23.5^{\circ} \cdot \cos \left[(264+10) \dfrac{360}{365}\right] \\
\text { Angle of sun }=70^{\circ}+-23.5^{\circ}(0.0043) \\
\text { Angle of sun }=70.10^{\circ}
\end{array}\)
Using inverse trigonometric functions
1. A tower, 28.4 feet high, must be secured with a guy wire anchored 5 feet from the base of the tower. What angle will the guy wire make with the ground?
Draw a picture.
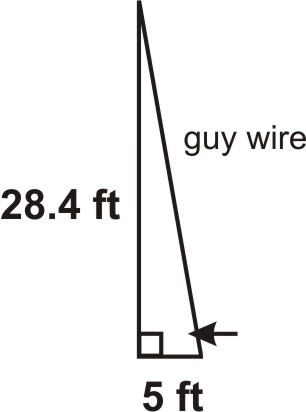
\(\begin{aligned}
\tan \theta &=\dfrac{o p p}{a d j} \\
\tan \theta &=\dfrac{28.4}{5} \\
\tan \theta &=5.68 \\
\tan ^{-1}(\tan \theta) &=\tan ^{-1}(5.68) \\
\theta &=80.02^{\circ}
\end{aligned}\)
The following problem that involves functions and their inverses will be solved using the property \(f(f^{−1}(x))=f^{−1}(f(x))\). In addition, technology will also be used to complete the solution.
2. In the main concourse of the local arena, there are several viewing screens that are available to watch so that you do not miss any of the action on the ice. The bottom of one screen is 3 feet above eye level and the screen itself is 7 feet high. The angle of vision (inclination) is formed by looking at both the bottom and top of the screen.
Sketch a picture to represent this problem.
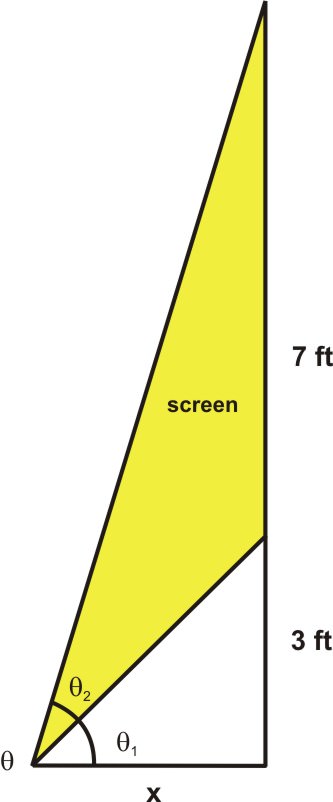
Calculate the measure of the angle of vision that results from looking at the bottom and then the top of the screen. At what distance from the screen does the maximum value for the angle of vision occur?
\(\begin{aligned}
\theta_{2} &=\tan \theta-\tan \theta_{1} \\
\tan \theta &=\dfrac{10}{x} \text { and } \tan \theta_{1}=\dfrac{3}{x} \\
\theta_{2} &=\tan ^{-1}\left(\dfrac{10}{x}\right)-\tan ^{-1}\left(\dfrac{3}{x}\right)
\end{aligned}\)
To determine these values, use a graphing calculator and the trace function to determine when the actual maximum occurs.

From the graph, it can be seen that the maximum occurs when \(x\approx 5.59\text{ ft}\). and \(\theta\approx 32.57^{\circ}\).
Earlier, you were asked to calculate the angle that you need to walk with respect to due East.
Solution
You can set up a triangle that matches the physical situation of this problem. Here is what it should look like:
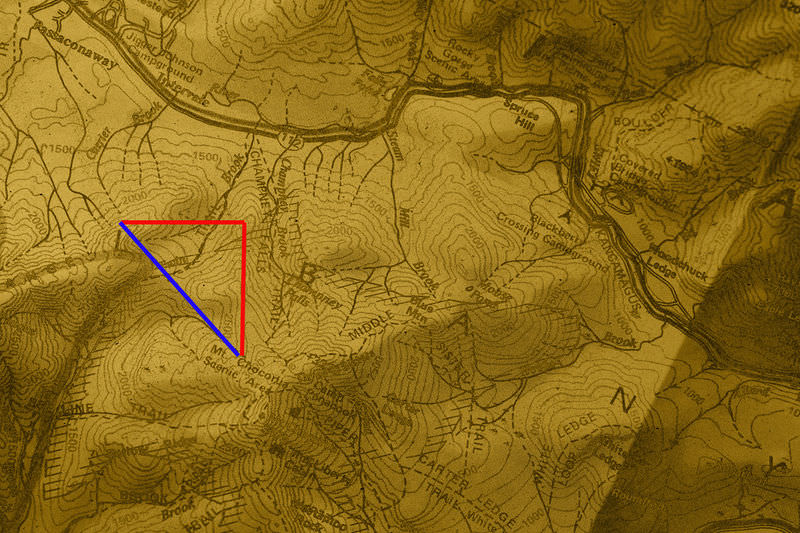
Using the tangent function, you can solve for the angle you need to find:
\(\begin{aligned} \theta&= \tan^{−1}\left(\dfrac{3}{−2.5}\right) \\ \theta&=−50.19 \end{aligned}\)
The intensity of a certain type of polarized light is given by the equation \(I=I_0 \sin 2\theta \cos 2\theta\).
Solve for \(\theta\).
Solution
\(\begin{aligned}
I &=I_{0} \sin 2 \theta \cos 2 \theta \\
\dfrac{I}{I_{0}} &=\dfrac{I_{0}}{I_{0}} \sin 2 \theta \cos 2 \theta \\
\dfrac{I}{I_{0}} &=\sin 2 \theta \cos 2 \theta \\
\dfrac{2 I}{I_{0}} &=2 \sin 2 \theta \cos 2 \theta \\
\dfrac{2 I}{I_{0}} &=\sin 4 \theta \\
\sin ^{-1} \dfrac{2 I}{I_{0}} &=4 \theta \\
\dfrac{1}{4} \sin ^{-1} \dfrac{2 I}{I_{0}} &=\theta
\end{aligned}\)
The following diagram represents the ends of a water trough. The ends are actually isosceles trapezoids, and the length of the trough from end-to-end is ten feet. Determine the maximum volume of the trough and the value of \(\theta\) that maximizes that volume.
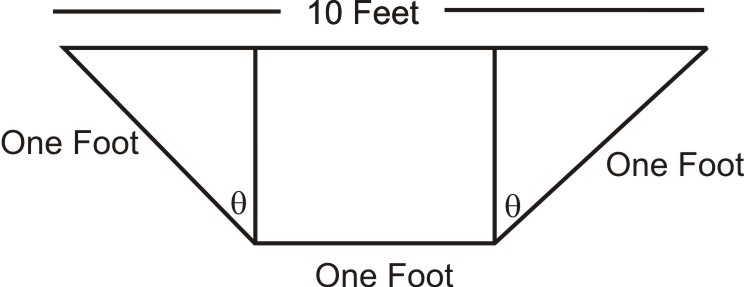
Solution
The volume is 10 feet times the area of the end. The end consists of two congruent right triangles and one rectangle. The area of each right triangle is \(\dfrac{1}{2}(\sin \theta)(\cos \theta)\) and that of the rectangle is \((1)(\cos \theta)\). This means that the volume can be determined by the function \(V(\theta)=10(\cos \theta+ \sin \theta \cos\theta)\), and this function can be graphed as follows to find the maximum volume and the angle \(\theta\) where it occurs.
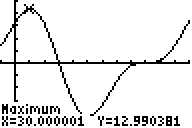
Therefore, the maximum volume is approximately 13 cubic feet and occurs when \(\theta\) is about \(30^{\circ}\).
A boat is docked at the end of a 10 foot pier. The boat leaves the pier and drops anchor 230 feet away 3 feet straight out from shore (which is perpendicular to the pier). What was the bearing of the boat from a line drawn from the end of the pier through the foot of the pier?
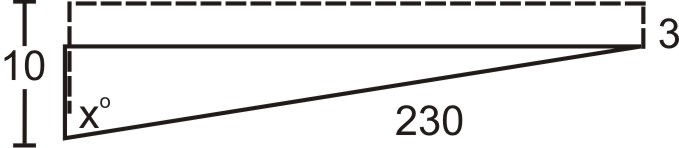
Solution
\(\begin{aligned} \cos x &=\dfrac{7}{230}\rightarrow x=\cos^{−1} \dfrac{7}{230}\\ x&= 88.26^{\circ} \end{aligned}\)
Review
- The distance from a boat to a lighthouse is 100 feet and the lighthouse is 120 feet tall. What is the angle of depression from the top of the Lighthouse to the boat.
- You are standing 100 feet from an arch that is 68 feet tall. At what angle do you have to look up to see the top of the arch? Assume you are 5 feet tall.
- The angle of elevation of the top of a church to a point 100 feet away from the base is \(60^{\circ}\). Find the height of the church.
You are standing looking at a large painting on the wall. The bottom of the painting is 1 foot above your eye level. The painting is 10 feet tall. Assume you are standing \(x\) feet from the painting and that angle \theta is formed by the lines of vision to the bottom and to the top of the painting.
- Draw a picture to represent this situation.
- Solve for \(\theta\) in terms of \(x\).
- If you are standing 10 feet from the painting, what is \theta?
- If \(\theta=30^{\circ}\), how far are you standing from the wall (to the nearest foot)?
You are watching a hot-air balloon that was 300 feet from you when it started rising from the ground. Assume the height of the balloon is \(x\) and \(\theta\) is the angle of elevation from the ground where you are standing up to the balloon.
- Solve for \(x\) in terms of \(\theta\).
- Solve for \(\theta\) in terms of \(x\).
- What is the angle of elevation when the hot-air balloon is 500 feet above the ground?
- How high above the ground is the balloon when the angle of elevation is 80^{\circ}?
Recall that if the latitude of the location is known, then the following formula can be used to calculate the angle of inclination of the sun on any given date of the year:
\(\text{Angle of sun}=90^{\circ}−\text{latitude}+−23.5^{\circ} \cdot cos[(N+10)\dfrac{360}{365}]\) where \(N\) represents the number of the day of the year that corresponds to the date of the year.
- Determine the measurement of the sun’s angle of inclination for a building located at a latitude of \(30^{\circ}\), April \(12^{th}\), the \(102^{th}\) day of the year.
- Determine the measurement of the sun’s angle of inclination for a building located at a latitude of \(50^{\circ}\), August \(14^{th}\), the \(226^{th}\) day of the year.
- A tower, 50 feet high, is secured with a guy wire anchored 8 feet from the base of the tower. What angle will the guy wire make with the ground?
- A 30 foot tall flagpole casts a 12 foot shadow. What is the angle that the sun hits the flagpole?
Review (Answers)
To see the Review answers, open this PDF file and look for section 4.10.
Vocabulary
| Term | Definition |
|---|---|
| inverse trigonometric function | An inverse trigonometric function is a function that reverses a trigonometric function, leaving the argument of the original trigonometric function as a result. |
Additional Resources
Video: Height and Distance Word Problem Application of Trigonometry

