5.13: Trapezoids
- Page ID
- 4997
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Determine unknown angle measurements of quadrilaterals with exactly one pair of parallel sides.
A trapezoid is a quadrilateral with exactly one pair of parallel sides.
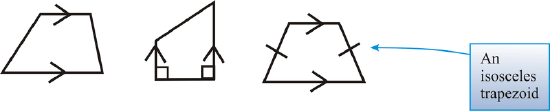
An isosceles trapezoid is a trapezoid where the non-parallel sides are congruent.
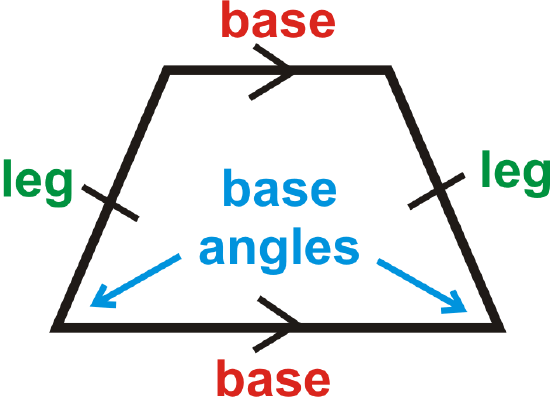
The base angles of an isosceles trapezoid are congruent. If \(\(ABCD\)\) is an isosceles trapezoid, then \(\angle A\cong \angle B\) and \(\angle C\cong \angle D\).
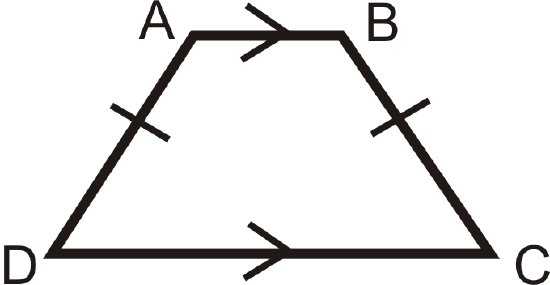
The converse is also true. If a trapezoid has congruent base angles, then it is an isosceles trapezoid. The diagonals of an isosceles trapezoid are also congruent. The midsegment (of a trapezoid) is a line segment that connects the midpoints of the non-parallel sides:
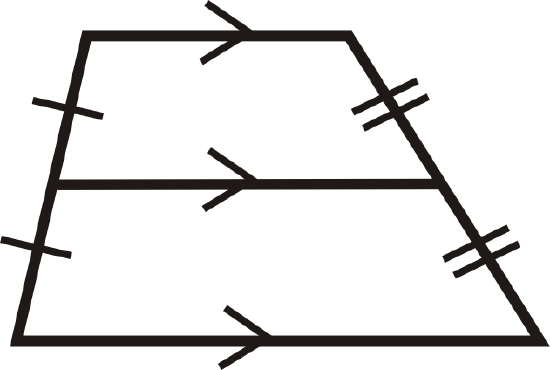
There is only one midsegment in a trapezoid. It will be parallel to the bases because it is located halfway between them.
Midsegment Theorem: The length of the midsegment of a trapezoid is the average of the lengths of the bases.
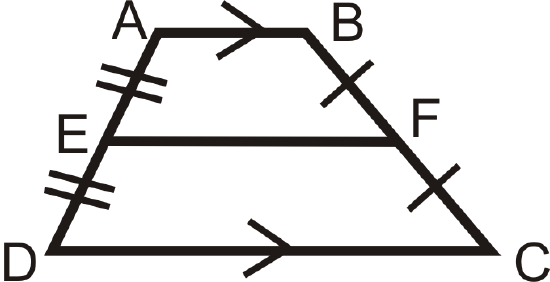
If \(\overline{EF}\) is the midsegment, then \(EF=\dfrac{AB+CD}{2}\).
What if you were told that the polygon \(ABCD\) is an isosceles trapezoid and that one of its base angles measures \(38^{\circ}\)? What can you conclude about its other base angle?
For Examples 1 and 2, use the following information:
\(\(TRAP\)\) is an isosceles trapezoid.
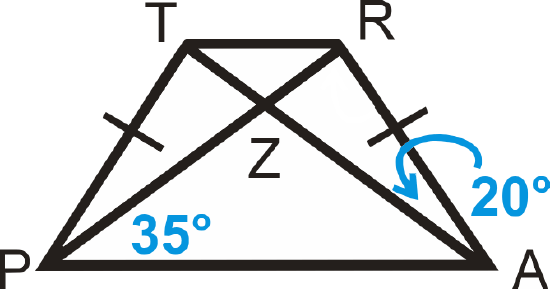
Example \(\PageIndex{1}\)
Find \(m\angle TPA\).
Solution
\(\angle TPZ\cong \angle RAZ\) so \(m\angle TPA=20^{\circ} +35^{\circ} =55^{\circ}\).
Example \(\PageIndex{2}\)
Find \(m\angle ZRA\).
Solution
Since \(m\angle PZA=110^{\circ}\), \(m\angle RZA=70^{\circ}\) because they form a linear pair. By the Triangle Sum Theorem, \(m\angle ZRA=90^{\circ}\).
Example \(\PageIndex{3}\)
Look at trapezoid \(TRAP\) below. What is \(m\angle A\)?
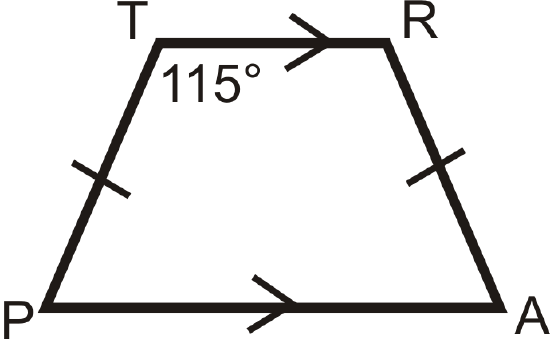
Solution
\(TRAP\) is an isosceles trapezoid. \(m\angle R=115^{\circ}\) also.
To find \(m\angle , set up an equation.
\(\begin{aligned}
115^{\circ}+115^{\circ}+m \angle A+m \angle P &=360^{\circ} \\
230^{\circ}+2 m \angle A &=360^{\circ} \quad \rightarrow m \angle A=m \angle P \\
2 m \angle A &=130^{\circ} \\
m \angle A &=65^{\circ}
\end{aligned}\)
Notice that \(m\angle R+m\angle A=115^{\circ} +65^{\circ} =180^{\circ}\). These angles will always be supplementary because of the Consecutive Interior Angles Theorem.
Example \(\PageIndex{4}\)
Is \(ZOID\) an isosceles trapezoid? How do you know?
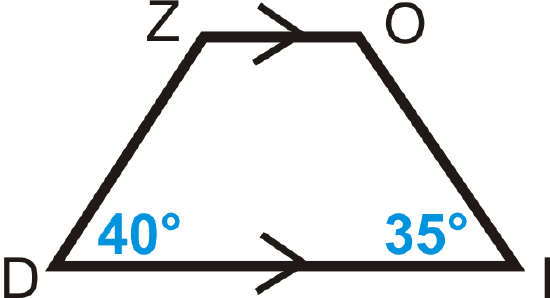
Solution
\(40^{\circ} \neq 35^{\circ}\), \(ZOID\) is not an isosceles trapezoid.
Example \(\PageIndex{5}\)
Find \(x\). All figures are trapezoids with the midsegment marked as indicated.
-
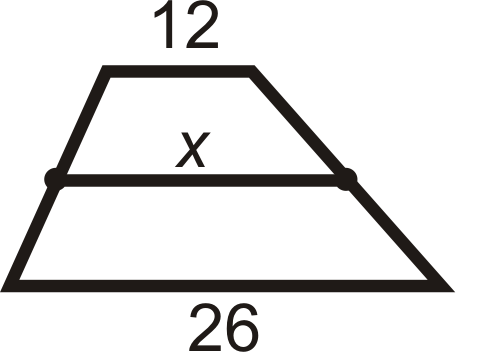
Figure \(\PageIndex{10}\)
-
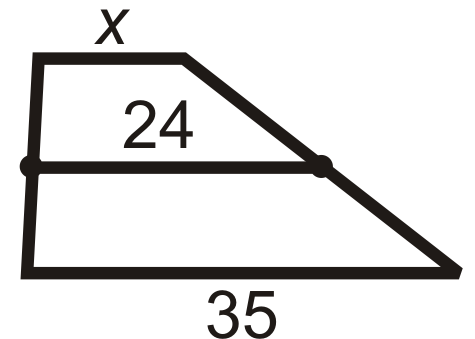
Figure \(\PageIndex{10}\) -
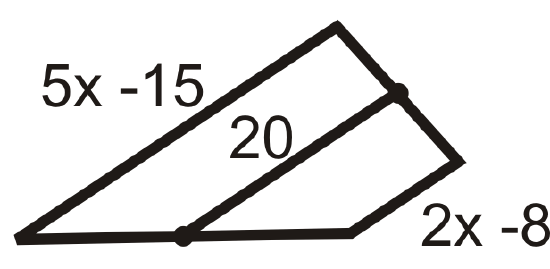
Figure \(\PageIndex{11}\)
Solution
- \(x\) is the average of 12 and 26. \(\dfrac{12+26}{2}=\dfrac{38}{2}=19\)
- 24 is the average of \(x\) and 35.
\(\begin{aligned} \dfrac{x+35}{2}&=24 \\ x+35&=48 \\ x&=13 \end{aligned}\)
- 20 is the average of \(5x−15\) and \(2x−8\).
\(\begin{aligned} \dfrac{5x−15+2x−8}{2}&=20 \\ 7x−23&=40 \\ 7x&=63 \\ x&=9 \end{aligned}\)
Review
1. Can the parallel sides of a trapezoid be congruent? Why or why not?
For questions 2-8, find the length of the midsegment or missing side.
-
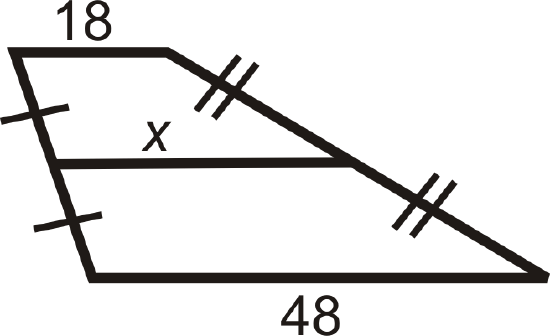
Figure \(\PageIndex{12}\) -
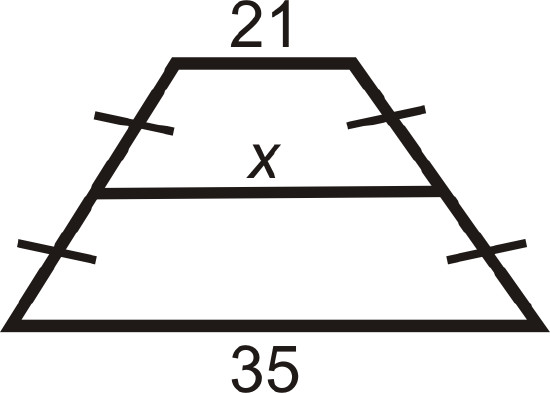
Figure \(\PageIndex{13}\) -
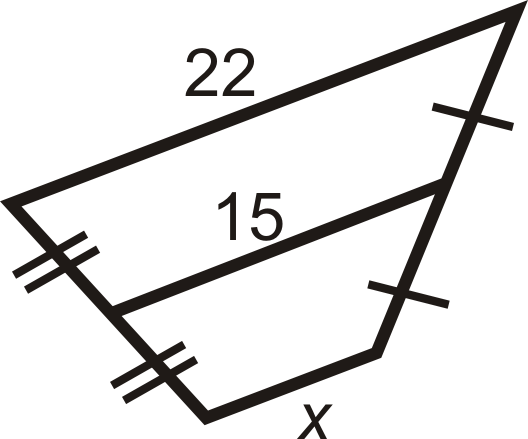
Figure \(\PageIndex{14}\) -
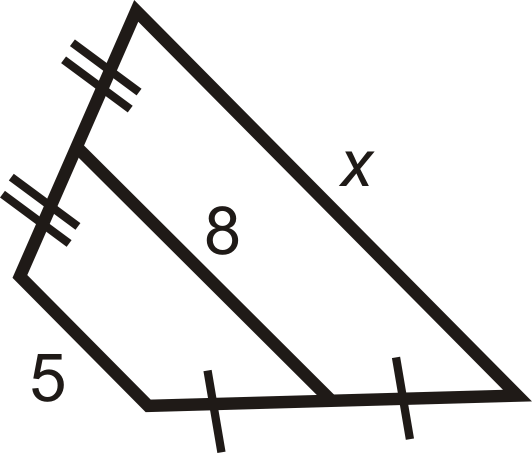
Figure \(\PageIndex{15}\) -
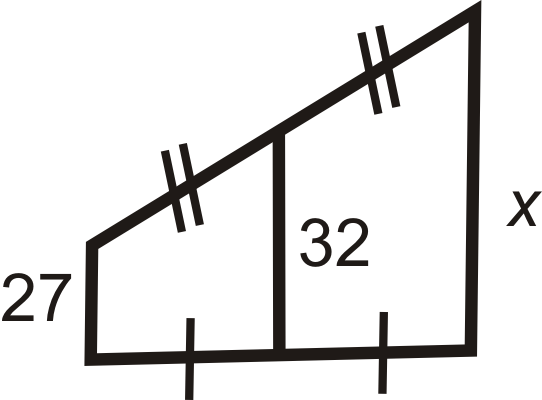
Figure \(\PageIndex{16}\) -
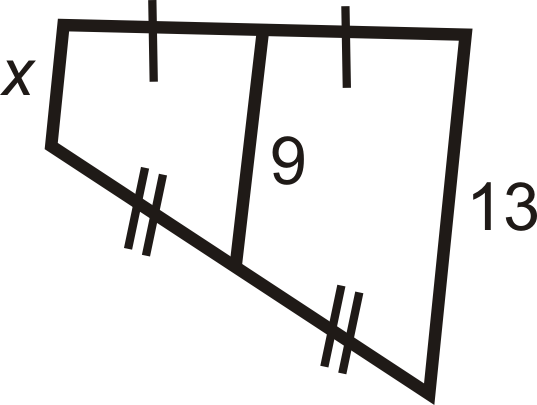
Figure \(\PageIndex{17}\)
Find the value of the missing variable(s).
-
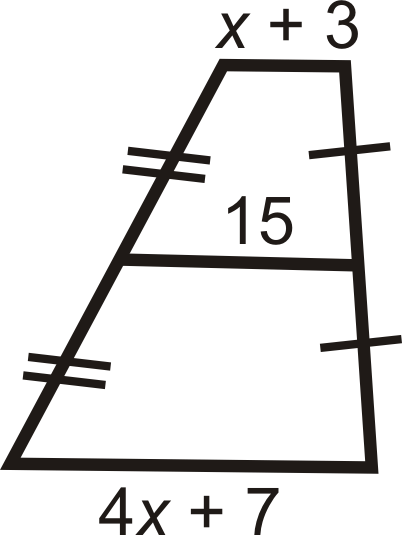
Figure \(\PageIndex{18}\)
Find the lengths of the diagonals of the trapezoids below to determine if it is isosceles.
- A(−3,2), B(1,3), C(3,−1), D(−4,−2)
- A(−3,3), B(2,−2), C(−6,−6), D(−7,1)
Review (Answers)
To see the Review answers, open this PDF file and look for section 6.6.
Vocabulary
| Term | Definition |
|---|---|
| isosceles trapezoid | An isosceles trapezoid is a trapezoid where the non-parallel sides are congruent. |
| midsegment (of a trapezoid) | A line segment that connects the midpoints of the non-parallel sides. |
| trapezoid | A quadrilateral with exactly one pair of parallel sides. |
| Diagonal | A diagonal is a line segment in a polygon that connects nonconsecutive vertices |
| midsegment | A midsegment connects the midpoints of two sides of a triangle or the non-parallel sides of a trapezoid. |
Additional Resources
Interactive Element
Video: Trapezoids Examples - Basic
Activities: Trapezoids Discussion Questions
Study Aids: Trapezoids and Kites Study Guide
Practice: Trapezoids
Real World: Trapezoids in Timbuktu

