5.6: Unknown Dimensions of Squares and Rectangles
- Page ID
- 2151
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Compute linear measures, given edge or surface measures of rectilinear quadrilaterals.

Andrea is out Christmas shopping with her mom and spots a sale on Christmas lights. She asks her mom if she can get some to string around the perimeter of her bedroom. Her mom agrees, so they look at the packages to try to figure out how many they will need. Andrea's mom can't remember the exact dimensions of Andrea's room, but she remembers that it is 81 square feet and is a square. How can Andrea figure out how many feet of Christmas lights she needs?
In this concept, you will learn how to use formulas to solve for unknown dimensions when given perimeter or area.
Finding Unknown Dimensions Using Formulas
Perimeter is the distance around a figure. Area is the number of square units contained inside a figure. The perimeters and areas of rectangles and squares can be found using the formulas below.
- Rectangle Perimeter: \(P=2l+2w\)
- Square Perimeter: \(P=4s\)
- Rectangle Area: \(A=lw\)
- Square Area: \(A=s^2\)
An equation is a mathematical sentence that says that two mathematical expressions are equal. The perimeter and area formulas above are examples of equations. The variables in these equations are \(P\), \(A\), \(l\), \(w\), and \(s\).
Sometimes you will know the area or perimeter of a rectangle or a square, but not know information about all of its sides. In this case, you can substitute the information you know into the relevant formula and solve for the unknown value. Remember that when you solve an equation you are looking for the value of the variable that makes both sides of the equation equal.
Here is an example.
The width of a rectangle is 10 feet and the perimeter is 50 feet. What is the length of the rectangle?
First, figure out which formula is relevant. This question is about the perimeter of a rectangle, so you will be using the rectangle perimeter formula.
\(P=2l+2w\)
Next, figure out which variables you have values for and which variable you are solving for. The problem says that the width is 10 feet, so w=10. The problem also says that the perimeter is 50 feet, so \(P=50\). You are solving for the length.
\( \begin{aligned} P&=50 \\ l&=?\\ w&=10\end{aligned}\)
Now, substitute the values for \(P\) and \(w\) into the formula and simplify.
Next, solve the equation. Remember you are looking for the value of l that will make both sides of the equation equal. First, figure out the value of the \(2l\) in the equation. Ask yourself a question.
"50 is equal to what number plus 20?"
Then, answer your question. 30 plus 20 is equal to 50, so \(2l\) must be equal to 30.
Now, you have a simpler equation to solve.
\(2l=30\)
Next, ask yourself another question.
"2 times what number is equal to 30?"
Finally, answer your question. 2 times 15 is equal to 30, so l must be equal to 15.
The answer is that the length of the rectangle is 15 feet.
You can check your answer by substituting all three values into the rectangle perimeter formula, evaluating, and making sure both sides of the equation end up equal to each other.
The answer is correct.
Here is another example.
If the area of a square is 144 square miles, what is the length of one of the sides of the square?
First, figure out which formula is relevant. This question is about the area of a square, so you will be using the square area formula.
\(A=s^2\)
Next, figure out which variable you have a value for and which variable you are solving for. The problem says that the area is 144 square miles, so A=144. You are solving for the length of the side.
Now, substitute the value for A into the formula.
Next, solve the equation. Remember you are looking for the value of s that will make both sides of the equation equal. Ask yourself a question.
"144 is equal to what number times itself?"
Then, answer your question. 12 times 12 is equal to 144, so s must be equal to 12.
The answer is that the side length of the square is 12 miles.
Now, check your answer by substituting both values into the square area formula, evaluating, and making sure both sides of the equation end up equal to each other.
The answer is correct.
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Andrea and the Christmas lights.
She's buying some to string around the perimeter of her room and needs to know how many feet of lights to buy. She knows her square room has an area of 81 square feet.
Solution
First, figure out the length of each side of her room. Her room is a square and you know its area, so you will be using the square area formula.
\(A=s^2\)
Now, you know that the area of the square is 81 square feet, so \(A=81\). Substitute this value for A into the formula.
Next, ask yourself a question to help solve the equation.
"81 is equal to what number times itself?"
Then, answer your question. 9 times 9 is equal to 81, so s must be equal to 9. Each side of Andrea's room is 9 feet.
Now, you need to figure out the perimeter of Andrea's room so Andrea will know how many feet of lights she needs. You know the room is a square with a side length of 9 feet. Substitute s=9 into the square perimeter formula.
The answer is that the perimeter of her room is 36 feet, so she needs 36 feet of lights.
Example \(\PageIndex{2}\)
The Hegazzi family is designing a summer garden based on the model shown below. The bottom of the plot is a square and the top of the plot is a rectangle. If the total area of both plots in the garden is 139 square feet, what is the length of one side of the square plot (indicated with a question mark below)?
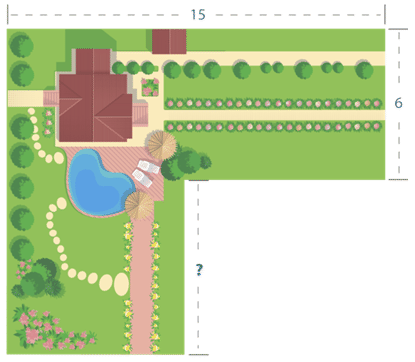
Solution
First, use the given information to find the area of the rectangle plot. You will then use this information to help you to find the area of the square plot, which will allow you to find the side length of the square plot.
The rectangle has a length of 15 feet and a width of 6 feet. The formula to find the area of a rectangle is \(A=lw\). Substitute the values for the length and the width of the rectangle into the formula and evaluate to find the area.
Next, find the area of the square plot. You know that the total area is 139 square feet and the area of the rectangle is 90 square feet. You also know that the total area is equal to the rectangle area plus the square area. Substitute the values that you know into this relationship.
Now, solve the equation by asking yourself a question.
"139 is equal to 90 plus what number?"
Next, answer the question. 90 plus 10 is equal to 100. 100 plus 39 is equal to 139. So 90 plus 49 must equal 139. The area of the square plot is 49 square feet.
Now, use the area of the square plot to help you to find the side length of the square plot. Substitute the value for \(A\) into the square area formula.
Next, solve the equation.
"49 is equal to what number times itself?"
Then, answer your question. 7 times 7 is equal to 49, so s must be equal to 7.
The answer is that the side length of the square plot is 7 feet.
Example \(\PageIndex{3}\)
If the perimeter of a rectangle is 30 feet, with a length of 9 feet, what is the width of the rectangle?
Solution
First, figure out which formula is relevant. This question is about the perimeter of a rectangle, so you will be using the rectangle perimeter formula.
\(P=2l+2w\)
Next, figure out which variables you have values for and which variable you are solving for. The problem says that the perimeter is 30 feet, so P=30\). The problem also says the length is 9 feet, so l=9\). You are solving for the width.
\(\begin{aligned} P&=30 \\ l&=9 \\ w&=? \end{aligned}\)
Now, substitute the values for P and l into the formula and simplify.
Next, solve the equation. First, figure out the value of the \(2w\) in the equation. Ask yourself a question.
"30 is equal to 18 plus what number?"
Then, answer your question. 18 plus 12 is equal to 30, so \(2w\) must be equal to 12.
Now, you have a simpler equation to solve.
\(2w=12\)
Next, ask yourself another question.
"2 times what number is equal to 12?"
Finally, answer your question. 2 times 6 is equal to 12, so w must be equal to 6.
The answer is that the width of the rectangle is 6 feet.
Now, check your answer by substituting all three values into the rectangle perimeter formula, evaluating, and making sure both sides of the equation end up equal to each other.
The answer is correct.
Example \(\PageIndex{4}\)
If the area of a square is 225 square feet, what is the length of one of its sides?
Solution
First, figure out which formula is relevant. This question is about the area of a square, so you will be using the square area formula.
\(A=s^2\)
Next, figure out which variable you have a value for and which variable you are solving for. The problem says that the area is 225 square feet, so \(A=225\). You are solving for the length of the side.
Now, substitute the value for A into the formula.
Next, solve the equation by asking yourself a question.
"225 is equal to what number times itself?"
Then, answer your question. 15 times 15 is equal to 225, so s must be equal to 15.
The answer is that the side length of the square is 15 feet.
Now, check your answer by substituting both values into the square area formula, evaluating, and making sure both sides of the equation end up equal to each other.
The answer is correct.
Example \(\PageIndex{5}\)
If the perimeter of a square is 24 meters, what is the length of one of the sides?
Solution
First, figure out which formula is relevant. This question is about the perimeter of a square, so you will be using the square perimeter formula.
\(P=4s\)
Next, figure out which variable you have a value for and which variable you are solving for. The problem says that the perimeter is 24 meters, so \(P=24\). You are solving for the length of the side.
Now, substitute the value for \(P\) into the formula.
Next, solve the equation by asking yourself a question.
"24 is equal to 4 times what number?"
Then, answer your question. 4 times 6 is equal to 24, so s must be equal to 6.
The answer is that the side length of the square is 6 meters.
Now, check your answer by substituting both values into the square perimeter formula, evaluating, and making sure both sides of the equation end up equal to each other.
The answer is correct.
Review
Given the area, find the side length for each square.
- \(A=16\text{ sq. ft. } \)
- \(A=64\text{ sq. m. } \)
- \(A=100\text{ sq. miles }\)
- \(A=121\text{ sq. inches } \)
- \(A=144\text{ sq. ft. } \)
Given the area and length, find the width of each rectangle.
- \(A=24\text{ sq. feet },\text{ length }=8\text{ feet } \)
- \(A=48 \text{ sq. feet },\text{ length }=12\text{ feet } \)
- \(A=64\text{ sq. feet },\text{ length }=10\text{ feet } \)
- \(A=120\text{ sq. meters },\text{ length }=40\text{ meters } \)
- \(A=130\text{ sq. feet },\text{ length }=13\text{ feet } \)
- \(A=90\text{ sq. inches },\text{ length }=45\text{ inches } \)
Given the perimeter, find the side length of each square.
- \(P=48\text{ inches } \)
- \(P=64\text{ inches } \)
- \(P=90\text{ inches } \)
- \(P=35\text{ feet } \)
Review (Answers)
To see the Review answers, open this PDF file and look for section 1.15.
Vocabulary
| Term | Definition |
|---|---|
| Area | Area is the space within the perimeter of a two-dimensional figure. |
| Measurement | A measurement is the weight, height, length or size of something. |
Additional Resources
Video: Determine the Area of a Rectangle Involving Whole Numbers
Practice: Unknown Dimensions of Squares and Rectangles
Real World: Yard Waste

