5.5: Area of Squares and Rectangles
- Page ID
- 2153
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Find the area of squares and rectangles using formulas: base times height and side squared.

Allen bought a new house and is planning to replace the carpet in two of the bedrooms. One bedroom is a shaped like a square and the other is rectangular. He needs to figure out how much carpet is needed to cover both bedroom floors.
The square bedroom has side lengths of 9 feet.

The rectangular bedroom has a length of 12 feet and a width of 8 feet.

In order for Allen to figure out how much carpet he needs to buy for these two bedrooms, he needs to find the area of each bedroom.
In this concept, you will learn how to find the area of squares and rectangles.
Area
The inside space of a figure is known as the area of the figure. Carpeting a floor, grass on the ground, or anything else covering the space inside of a figure are all examples of area.
There is a formula for finding the area of different shapes. In this concept, this concept will show you how to find the area of both squares and rectangles.
This is the formula used to find the area of a square:
\(A=s\cdot s\)
Remember, the dot is another symbol for multiplication. To figure out the area of the square, multiply one side times the other side. Since all sides in a square are equal, the two numbers will be the same. The unit of measurement is kept in the equation to help you remember what the correct label should be.
Here is how to use the formula for finding the area of a square:
\(A=6\text{ ft }\cdot 6\text{ ft }\)
Now, think of the equation as multiplying two different things; the numbers and the units of measurement.
\(A=6\cdot 6\)
\(A=ft\cdot\text{ ft }\)
Solve both equations.
\(A=6\times 6=36\)
\(A=ft\times\text{ ft }=ft^2\)
Think back to what you know about exponents. When you multiply two of the same thing together, you can write it in exponential form. Another way to label area is to write square feet (sq. ft.).
The answer is \(36\: sq.\:\text{ ft }.\) or \(36\:\text{ ft }^2\)
This is the formula used to find the area of a rectangle:
\(A=lw\)
To find the area of a rectangle, use the measurements for length and width instead of side length. These numbers may be different from each other because not all rectangles have the same side lengths like squares do.

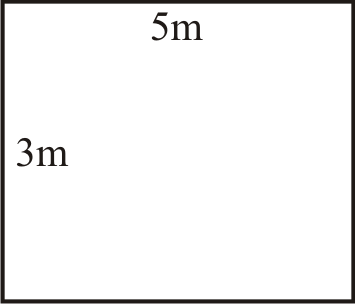
This rectangle measures a length of 5 meters and a width of 3 meters. Just like the area formula for a square, multiply those two numbers to find the area of the rectangle. Remember, two variables next to each other in an equation indicate multiplication, just like the dot symbol or traditional multiplication symbol. The symbols will be used interchangeably.
To find the area of a rectangle, multiply length times width.
\(A=5\text{ m }\cdot 3\text{ m }\)
\(A=5\times 3\)
\(A=meters\times meters\)
The formula shows 5 meters times 3 meters. Multiply the measurement part (\(5 \times 3\)), then multiply the units of measurement.
The answer is \(15\text{ sq. m }\) or \(15 \text{ m}^2\).
The label for area of a rectangle is similar to the label for area of a square from above. The label can be written in exponential form or written in abbreviation.
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Allen and his new house that he wants to re-carpet.
The dimensions of Allen's two bedrooms are given in the beginning of the concept. His square bedroom has side lengths of 9 feet. The other room is a rectangle with dimensions of 12 feet by 8 feet. To begin solving this problem, find the area of each of the bedrooms.
Solution
The square bedroom has a side length of 9 feet.
\(A=s\cdot s\)
\(A=9\times 9=81\text{ sq. feet }\)
The square bedroom has an area of 81 square feet.
The rectangular bedroom has a length of 12 feet and width of 8 feet.
\(A=12\:\text{ ft }\cdot 8\:\text{ ft }\)
\(A=12\times 8\)
\(A=feet\times feet\)
The rectangular bedroom has an area of 96 square feet.
Allen wants the total area of his two bedrooms to know how much carpet to buy, so add the two areas together.
\(81+96=177\text{ square feet }\)
The answer is 177 square feet.
Example \(\PageIndex{2}\)
Find the area of a rectangle with a length of 7\text{ ft }. and a width of 4\text{ ft }.
Solution
First, write out the equation
\(A=lw\)
\(A=7\:\text{ ft }\cdot 4\:\text{ ft }\)
Next, multiply the two numbers.
\(A=7\cdot 4=28\)
Then, multiply the units of measurement.
\(A=\text{ ft }\cdot\text{ ft }=\text{ ft}^2 \)
Now, put your answer together to show the final solution.
\(A=28\text{ ft }^2\)
The answer is \(28\: sq.\:\text{ ft }\).
Once you do more examples you may find yourself skipping the step of multiplying the units of measurement. This may become natural to square the unit of measurement for any area problem.
Example \(\PageIndex{3}\)
Find the area of a square with side lengths of 10 inches.
Solution
First, write your equation.
\(A=s\cdot s\)
\(A=10 \text{ in }\cdot 10 \text{ in}\)
Next, solve the equation by multiplying the two side lengths.
\( A=10\cdot 10=100\)
Then, write your final solution. Remember to write the squared unit of measurement after the numerical answer.
\(A=100\text{ in}^2\)
The answer is 100 sq. in.
Example \(\PageIndex{4}\)
Find the area of a rectangle with a length of 6 feet and a width of 5 feet.
Solution
First, write your equation.
\(A=lw\)
\(A=6\:\text{ ft }\cdot 5\:\text{ ft }\)
Next, solve the equation by multiplying the length times the width.
\(A=6\cdot 5=30\)
Then, write your final solution. Remember to write the squared unit of measurement after the numerical answer.
\( A=30\:\text{ ft }^2\)
The answer is 30 sq.\text{ ft }.
Example \(\PageIndex{5}\)
Find the area of a rectangle with a length of 9 meters and a width of 8 meters.
Solution
First, write your equation.
\(A=lw\)
\(A=9\text{ m }\cdot 8\text{ m }\)
Next, solve the equation by multiplying the length times the width.
\(A=9\cdot 8=72\)
Then, write your final solution. Remember to write the squared unit of measurement after the numerical answer.
\(A=72\text{ m }^2\)
The answer is 72 sq. m
Review
Find the area of each of the following figures. Make sure you label your answer correctly.
- A square with a side length of 6 inches.
- A square with a side length of 4 inches.
- A square with a side length of 8 centimeters.
- A square with a side length of 12 centimeters.
- A square with a side length of 9 meters.
- A rectangle with a length of 6 inches and a width of 4 inches.
- A rectangle with a length of 9 meters and a width of 3 meters.
- A rectangle with a length of 4 meters and a width of 2 meters.
- A rectangle with a length of 17 feet and a width of 12 feet.
- A rectangle with a length of 22 feet and a width of 18 feet.
- A square with a side length of 13 feet.
- A square with a side length of 18 feet.
- A square with a side length of 21 feet.
- A rectangle with a length of 18 feet and a width of 13 feet.
- A rectangle with a length of 60 feet and a width of 27 feet.
- A rectangle with a length of 57 feet and a width of 22 feet.
Resources
Additional Resource
Video: Determine the Area of a Rectangle Involving Whole Numbers
Practice: Area of Squares and Rectangles

