5.4: Perimeter of Squares and Rectangles
- Page ID
- 2150
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Use basic quadrilateral formulas to find total edge measures of rectilinear quadrilaterals.
Find Perimeter and Area of Squares and Rectangles Using Formulas

Raj has a small patch of land that he wants to turn into a vegetable garden. However, he wants to build a small fence around it before he plants anything. He knows that the area of the land is 240 square feet and that the length of one side is 15 feet. In order to build a fence, he needs to know the width of the land too. How can Raj write and solve an equation to determine the width of his future garden?
In this concept, you will learn to find the perimeter and area of squares and rectangles using formulas.
Perimeter and Area of Squares and Rectangles
A formula is a method that has been proven to work when solving specific types of problems.
Let’s explore some of those familiar formulas by looking at rectangles, squares, area and perimeter.
The perimeter of a figure is the distance around the figure. Perimeter is the sum of all of the sides in a square or rectangle. Since a rectangle has two sets of parallel sides, the formula for determining perimeter (\(P\)) of a rectangle is:
\(P=2L+2W\)
\(L=length\: and\: W=width\)
Let’s look at an example.
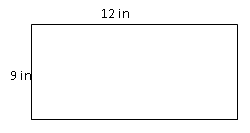
The rectangle above shows its dimensions. Find the perimeter.
First, substitute the values for the width (\(W\)) and the length (\(L\)) into the perimeter formula.
\(P=2(12)+2(9)\)
Next, complete the multiplication and addition to find the perimeter.
\(\begin{aligned} P&=2(12)+2(9) \\ P&=24+18 \\ P&=42\end{aligned}\)
The answer is 42.
The perimeter of the rectangle is 42 inches.
Area is the amount of square units inside the figure. Area is found by multiplying the length\times width. The formula for finding the area of a rectangle is:
\(A=L\times W\)
You can use the dimensions from the rectangle above to find the area of this rectangle.
First, fill the values for \(L\) and \(W\) into the formula for area.
\(\begin{aligned} A&=L\times W \\ A&=12\times 9\end{aligned}\)
Next, solve for the area by multiplying.
\(\begin{aligned} A&=12\times 9 \\ A&=108\end{aligned}\)
The answer is 108.
The area of the rectangle is \(108\: in^2\).
Notice that the unit of measurement for area is squared. That is because you multiplied a unit measure times itself: \(in\times in=in^2\). Area is always written in square units.
You can also find the perimeter and area of a square. Remember that a square has four equal sides given the symbol s. You can use the following formula for finding the perimeter of a square:
\(P=4s\)
Let’s look at an example.
A rectangle has a length of 12 feet and a perimeter of 72 feet. Write and solve an equation to determine the width of the rectangle.
First, substitute the values for the perimeter (\(P\)) and the length (\(L\)) into the perimeter formula.
\(72=2(12)+2W\)
Next, complete the multiplication.
\(72=24+2W\)
Then, subtract 24 from both sides to get your variable alone on the right side.
\(\begin{aligned} 72−24&=24−24+2W \\ 48 &=2W \end{aligned}\)
Then, multiply both sides by the reciprocal of 2 to isolate your variable.
\(\begin{aligned} \dfrac{1}{2}\times \dfrac{48}{1} &=\dfrac{1}{2}\times \dfrac{2W}{1} \\ \dfrac{48}{2}&=W \\ W&=24\end{aligned}\)
The answer is 24.
The width of the rectangle is 24 feet.
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Raj and his garden fence.
He knows that the area of the land is 240 square feet, the length of one side is 15 feet, and needs to know the width of the land.
Solution
First, substitute the values for the area and the side length into the area formula.
\(\begin{aligned} A&=L\times W \\ 240\text{ ft}^2 &=15\text{ ft } \times W\end{aligned}\)
Next, multiply both sides by the reciprocal of 15 in order to isolate the variable W.
\(\begin{aligned} \dfrac{1}{15}\times \dfrac{240}{1}&=\dfrac{1}{15}\times \dfrac{15}{1} \times W \\ W&=16 \end{aligned}\)
The answer is 16.
The width of Raj’s garden is 16 ft. Therefore the dimensions of the garden are 16 ft by 15 ft.
Example \(\PageIndex{2}\)
A square has a perimeter of 196 inches. Determine the length of one side of the square.
Solution
First, substitute the value for the perimeter (\(P\)) into the perimeter formula.
\(196=4s\)
Next, multiply both sides by the reciprocal of 4 to isolate your variable.
\(\begin{aligned} \dfrac{1}{4}\times \dfrac{196}{1}&=\dfrac{1}{4}\times \dfrac{4s}{1} \\ \dfrac{196}{4}&=s \\ s&=49 \end{aligned}\)
The answer is 49.
Example \(\PageIndex{3}\)
Find the perimeter of the following square if the side length is \(4.5\: inches\).
Solution
First, substitute the value for the side length into the perimeter formula.
\(\begin{aligned} P&=4s \\ P&=4(4.5) \end{aligned}\)
Next, multiply by 4 to solve for the perimeter.
\(\begin{aligned} P&=4(4.5) \\ P&=18 \end{aligned}\)
The answer is 18.
Example \(\PageIndex{4}\)
Can you find the area of the square in Example 1?
Solution
First, substitute the value for the side length into the area formula.
\(\begin{aligned} A&=s\times s \\ A&=4.5\times 4.5 \end{aligned}\)
Next, multiply to solve for the area.
\(\begin{aligned} A&=4.5\times 4.5 \\ A&=20.25\end{aligned}\)
The answer is 20.25.
The area of the square is \(20.25\text{ in}^2\).
Example \(\PageIndex{5}\)
A square has an area of 144 sq. meters. What is the side length?
Solution
First, substitute the value for the area into the area formula.
\(\begin{aligned} A&=s\times s \\ 144\text{ m}^2 &=s\times s \end{aligned}\)
Next, take the square root of the area to isolate \(s\). Remember that the opposite of square is square root.
\(\begin{aligned} 144&=s\times s \\ 144&=s^2 \\ s&=\sqrt{144} \\ s&=12 \end{aligned}\)
The answer is 12.
Review
Find the area and perimeter of each square or rectangle using formulas and the given dimensions. Each problem will have two answers.
- A square with a side length of 5 inches.
- A rectangle with a length of 5 inches and a width of 3 inches.
- A rectangle with a length of 8 cm and a width of 6 cm.
- A square with a side length of 11 feet.
- A rectangle with a length of 9 inches and a width of 4.5 inches.
- A square with a side length of 7 feet.
- A rectangle with a length of 12 meters and a width of 11 meters.
- A square with a side length of 13 meters.
- A rectangle with a length of 15 feet and a width of 8 feet.
- A square with a side length of 12.5 feet.
Find the missing side length given the area of each square.
- \(A=64\text{ in}^2\)
- \(A=36\text{ in}^2\)
- \(A=81\text{ m}^2\)
- \(A=100\text{ in}^2\)
- \(A=144\text{ ft}^2\)
- \(A=121\text{ cm}^2\)
- \(A=4\text{ mm}^2\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 1.13.
Vocabulary
| Term | Definition |
|---|---|
| Area | Area is the space within the perimeter of a two-dimensional figure. |
| Formula | A formula is a type of equation that shows the relationship between different variables. |
| Perimeter | Perimeter is the distance around a two-dimensional figure. |
| Square Unit | A Square Unit is a square with four sides that each measure 1 unit. |
Additional Resources
Interactive Element
Video: Determine the Area of a Rectangle Involving Whole Numbers
Practice: Perimeter of Squares and Rectangles
Real World: A Stitch in Time

