5.12: Estimation of Parallelogram Area in Scale Drawings
- Page ID
- 4996
Use a formula and a scale to determine actual dimensions from scale dimensions.
The town planned to put in a row of shuffleboard courts along a parallelogram-shaped piece of property near Jaxon’s home. If the drawing shows a parallelogram with a \(15′′\) base and a \(1′′\) height, and the scale is \(1\text{ inch }=12\text{ feet }\), how big is the entire area?
In this concept, you will learn to estimate the area of a parallelogram on a scale drawing.
Estimating the Area of a Parallelogram
A scale drawing is a drawing that uses a small measurement to represent the actual measurement.
If you are given the scale, you can use it to estimate the actual areas of a parallelogram.
For example:
Estimate the area of this garden.
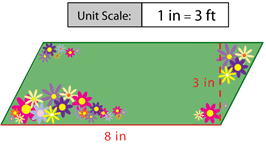
The formula for the area of a parallelogram is \(A=bh\).
If you multiply the dimensions given for the base and height on the scale drawing, you will get the square inches of the drawing, not the area of the actual garden. You will need to use the scale to convert the dimensions to their actual sizes.
First, the scale reads \(1\text{ in }=3\text{ ft }\). This means that each inch on the drawing represents 3 feet of actual ground. There are 3 feet per inch, so multiply the given base and height times 3.
\(8\text{ in }\times \dfrac{3\text{ ft }}{\text{ in }}\)
Writing the equation with two fractions, you can see that the inches cancel, and you are left with feet.
\(\dfrac{8 \text{ in }}{1}\times \dfrac{3\text{ ft }}{\text{ in }}=24\text{ ft }\)
This means that the actual base is 24\text{ ft }.
\(\dfrac{3 \text{ in }}{1}\times \dfrac{3\text{ ft }}{\text{ in }}=9\text{ ft }\)
This means that the actual height is 9 ft.
Next, round those values to the nearest 10.
\(24\approx 20\)
The approximate base is 20.
\(9\approx 10\)
The approximate height is 10.
Then, insert your approximations into the formula.
\(\begin{aligned} A&=bh \\ A&=20′\times 10′ \\ A&=200 \text{ sq ft } \end{aligned}\)
The answer is that the estimate is 200 square feet.
You can check your estimate by inserting the actual dimensions into the formula.
\(\begin{aligned} A&=bh \\ A&=24′\times 9′ \\ A&=216 \text{ sq ft } \end{aligned} \)
The actual area is 216 square feet.
\(216\approx 200\)
The estimate is reasonable.
Estimating can help you visualize the actual size of something and determine whether or not your answer is correct.
Remember that when rounding 4, 5, or 6, you may get a significantly higher or lower area than actual.
Example \(\PageIndex{1}\)
Earlier, you were give a problem about Jaxon and the blueprint of the shuffleboard court area.
Jaxon wants to estimate the size of the actual area and knows that the scale is 1 inch=12 feet. How many square feet will there be for the courts if the drawing has a base of 15 inches and a height of 1 inch?
Solution
First, determine the actual dimensions.
\(\begin{aligned} 15\text{ in }\times \dfrac{12\text{ ft }}{\text{ in }}&=180\text{ ft } \\ b&=180′ \\ 1\text{ in }\times \dfrac{12\text{ ft }}{\text{ in }}&=12\text{ ft } \\ h=12′ \end{aligned}\)
Next, round the values, and substitute into the formula.
\(\begin{aligned} A&=bh \\ A&=180′\times 10′ \\ A=1,800 \text{ sq ft } \end{aligned}\)
Jaxon’s estimate is 1,800 square feet.
Then, find the actual square footage by using the actual dimensions.
\(\begin{aligned} A&=180′\times 12′ \\ A&=2,160 \text{ sq ft }\end{aligned}\)
The actual area is 2,160 square feet.
Example \(\PageIndex{2}\)
Looking at the same drawing, use a scale of \(1′′=2\text{ feet }\).
Solution
First, the scale reads \(1\text{ in }=2\text{ ft }\), or 2 feet per inch, so multiply the given base and height times 2.
\(8\text{ in }\times \dfrac{2\text{ ft }}{\text{ in }}=16 \text{ ft }\)
The actual base is 16\text{ ft }.
\(3\text{ in }\times \dfrac{2\text{ ft }}{\text{ in }}=6 \text{ ft }\)
This means that the actual height is 6 ft.
Next, round those values to the nearest 10.
16 rounds to 20
The approximate base is 20.
6 rounds to 10
The approximate height is 10.
Then, insert your approximations into the formula.
\(\begin{aligned} A&=bh \\ A&=20′\times 10′ \\ A &=200 \text{ sq ft }\end{aligned}\)
The answer is that the estimate is 200 square feet.
You can check your estimate by inserting the actual dimensions into the formula.
\(\begin{aligned} A&=bh \\ A&=16′\times 6′ \\ A&=96 \text{ sq ft } \end{aligned}\)
The actual area is 96 square feet.
The estimate is high.
Example \(\PageIndex{3}\)
Use a scale of 1′′=4\text{ ft } to estimate the area that has a base of 6 inches and a height of 4 inches.
Solution
First, determine the actual dimensions.
\(\begin{aligned}6\text{ in }\times \dfrac{4\:\text{ ft }}{\text{ in }}&=24\:\text{ ft } \\ b&=24′ \\ 4\text{ in }\times \dfrac{4\text{ ft }}{\text{ in }}&=16\:\text{ ft } \\ h&=16′ \end{aligned}\)
Next, round the values, and substitute into the formula.
\(\begin{aligned} A&=20′\times 20′ \\ A&=400\text{ sq ft } \end{aligned}\)
The answer is that the estimate is 400 square feet.
Then, find the actual square footage by using the actual dimensions.
\(\begin{aligned}A&=24′\times 16′ \\ A&=384\text{ sq ft }\end{aligned}\)
The actual area is 384 square feet.
The estimate is reasonable.
Example \(\PageIndex{4}\)
Estimate the area of a parallelogram with a base of 59 inches and a height of 67 inches. Then solve for the actual area.
Solution
First, round the values, and substitute them into the formula.
\(\begin{aligned} A&=60′′\times 70′′ \\ A&=420 \text{ sq in }\end{aligned}\)
Next, use the actual dimensions in the formula.
\(\begin{aligned} A&=59′′\times 67′′ \\ A&=3,953 \text{ sq in }\end{aligned} \)
The answer is that the area is 3,953 square inches.
Example \(\PageIndex{5}\)
A parallelogram has a base of 12 cm and height of 9 cm. What is its area?
Solution
First, write the formula.
\(A=bh\)
Next, substitute.
\( A=12\text{ cm }\times 9\text{ cm }\)
Then, solve.
\( A=108\text{ sq cm }\)
The answer is 108 square centimeters.
If you rounded and multiplied in your head, your estimate should have been 100 square centimeters.
Review
For each parallelogram, find each new area using the scale \(1′′=2\text{ feet }\).
- Base of 6 inches, height of 4 inches
- Base of 8 inches, height of 6 inches
- Base of 4 inches, height of 4 inches
- Base of 5 inches, height of 4 inches
- Base of 6 inches, height of 6 inches
- Base of 10 inches, height of 8 inches
- Base of 11 inches, height of 12 inches
- Base of 15 inches, height of 9 inches
- Base of 15 inches, height of 12 inches
Solve each problem.
- A parallelogram has an area of 390 square centimeters. If its height is 15 cm, what is its base?
- What is the height of a parallelogram whose base is 28 inches and area is 1,176 square inches?
- Donna wants to cover her parallelogram-shaped crafts box in fabric. The base of the lid is 32.7 cm and the height is 12.2 cm. What is the area of the lid?
- John is planting grass in a patch of lawn that is shaped like a parallelogram. The height of the parallelogram is 34 feet. The other border is 65 feet. How many square feet of grass will John plant?
- Kara and Sharice are in a quilting competition. Both are stitching parallelogram-shaped quilts. So far Kara’s has an area of 2,278 square inches and a height of 44 inches. Sharice’s quilt has an area of 2,276 square inches and a height of 47 inches. Whose quilt is longer? By how many inches is it longer?
- Denise bought a picture frame in the shape of a parallelogram. The area of the picture frame is 36,795 square centimeters. If its height is 165 centimeters, what is its base?
Review (Answers)
To see the Review answers, open this PDF file and look for section 9.11.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Area | Area is the space within the perimeter of a two-dimensional figure. |
| Parallelogram | A parallelogram is a quadrilateral with two pairs of parallel sides. |
| Perimeter | Perimeter is the distance around a two-dimensional figure. |
| Scale Drawing | A scale drawing is a drawing that is done with a scale so that specific small units of measure represent larger units of measure. |
Additional Resources
Video: Area of a Parallelogram (Whole Numbers)
Practice: Estimation of Parallelogram Area in Scale Drawings