5.14: Area and Perimeter of Trapezoids
- Page ID
- 4998
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Area is the height times the average of the bases; perimeter is the sum of the sides.
A trapezoid is a quadrilateral with one pair of parallel sides. The parallel sides are called the bases and we will refer to the lengths of the bases as \(b_1\) and \(b_2\). The perpendicular distance between the parallel sides is the height of the trapezoid. The area of a trapezoid is \(A=\dfrac{1}{2}h(b_1+b_2)\) where \(h\) is always perpendicular to the bases.
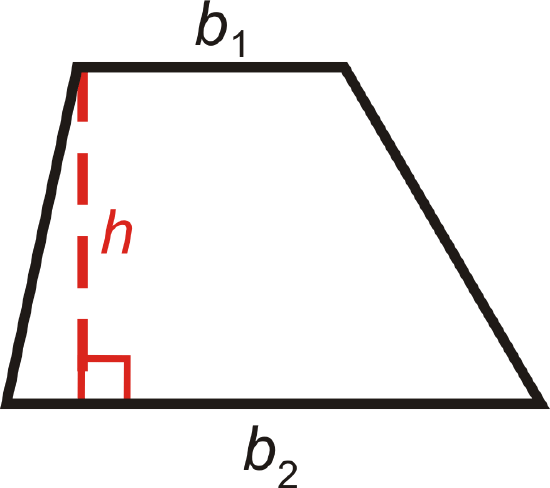
What if you were given a trapezoid and the size of its two bases as well as its height? How could you find the total distance around the trapezoid and the amount of space it takes up?
Example \(\PageIndex{1}\)
Find the area of the trapezoid.
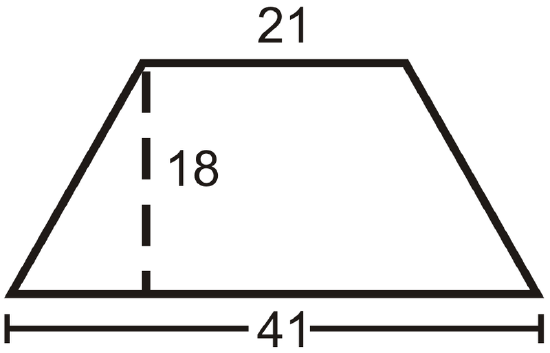
Solution
Use the formula for the area of a trapezoid.
\(\dfrac{1}{2}(18)(41+21)=558\text{ units}^2\)
Example \(\PageIndex{2}\)
Find the area of the trapezoid. Round your answers to the nearest hundredth.
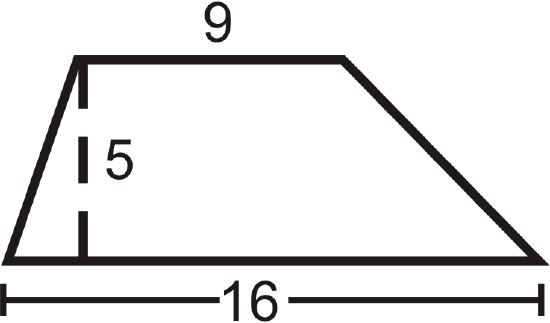
Solution
Use the formula for the area of a trapezoid.
\( \dfrac{1}{2}(5)(16+9)=62.5\text{ units}^2\)
Example \(\PageIndex{3}\)
Find the area of the trapezoid.
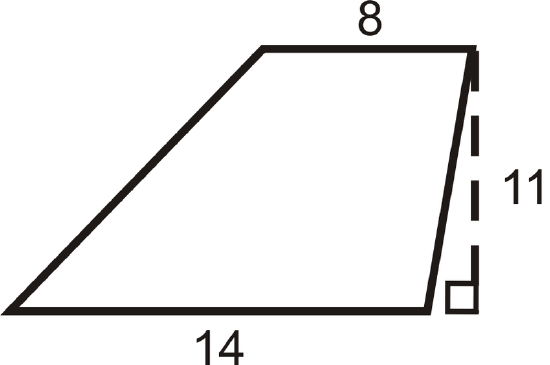
Solution
\(\begin{aligned} A&=\dfrac{1}{2}(11)(14+8) \\ A&=\dfrac{1}{2}(11)(22) \\ A&=121\text{ units}^2\end{aligned}\)
Example \(\PageIndex{4}\)
Find the area of the trapezoid.
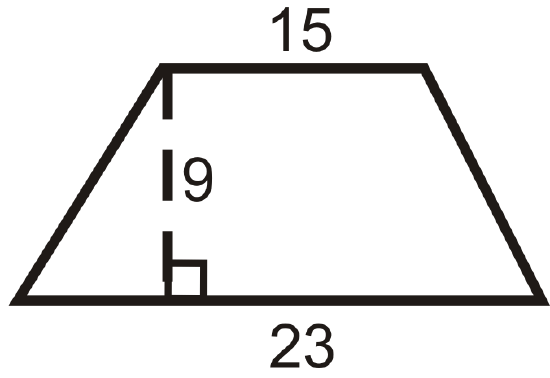
Solution
\(\begin{aligned} A&=\dfrac{1}{2}(9)(15+23) \\ A&=\dfrac{1}{2}(9)(38) \\ A&=171\text{ units}^2 \end{aligned}\)
Example \(\PageIndex{5}\)
Find the perimeter and area of the trapezoid.
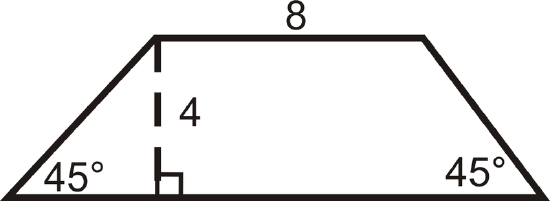
Solution
Even though we are not told the length of the second base, we can find it using special right triangles. Both triangles at the ends of this trapezoid are isosceles right triangles, so the hypotenuses are \(4\sqrt{2}\) and the other legs are of length 4.
\(\begin{aligned} P&=8+4\sqrt{2}+16+4\sqrt{2} &\qquad A&=\dfrac{1}{2}(4)(8+16) \\ P&=24+8\sqrt{2}\approx 35.3\text{ units} & A&=48\text{ units}^2 \end{aligned}\)
Review
Find the area and perimeter of the following shapes. Round your answers to the nearest hundredth.
-
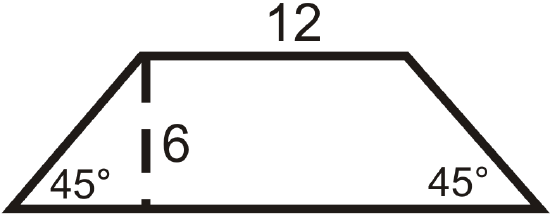
Figure \(\PageIndex{7}\) -
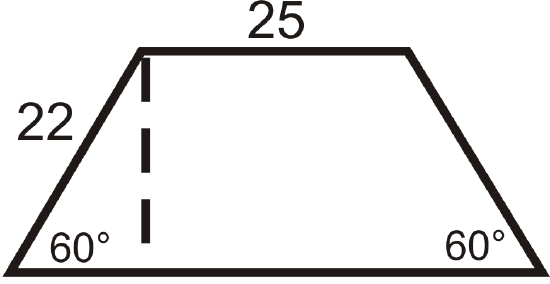
Figure \(\PageIndex{8}\)
Find the area of the following trapezoids.
- Trapezoid with bases 3 in and 7 in and height of 3 in.
- Trapezoid with bases 6 in and 8 in and height of 5 in.
- Trapezoid with bases 10 in and 26 in and height of 2 in.
- Trapezoid with bases 15 in and 12 in and height of 10 in.
- Trapezoid with bases 4 in and 23 in and height of 21 in.
- Trapezoid with bases 9 in and 4 in and height of 1 in.
- Trapezoid with bases 12 in and 8 in and height of 16 in.
- Trapezoid with bases 26 in and 14 in and height of 19 in.
Use the given figures to answer the questions.
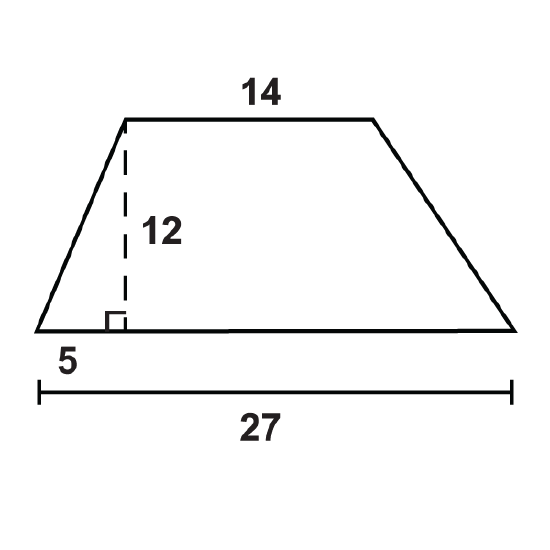
- What is the perimeter of the trapezoid?
- What is the area of the trapezoid?
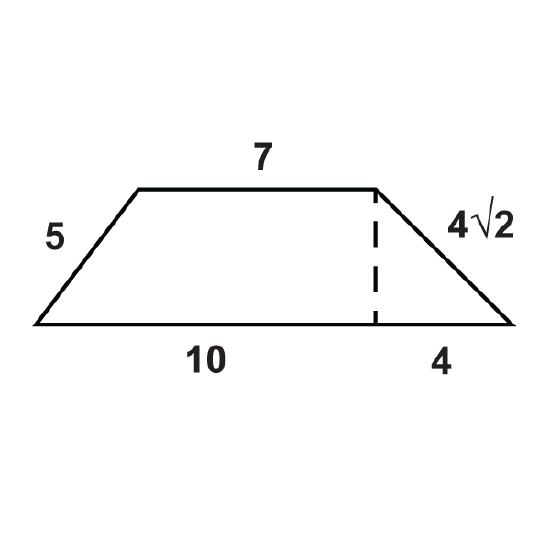
- What is the perimeter of the trapezoid?
- What is the area of the trapezoid?
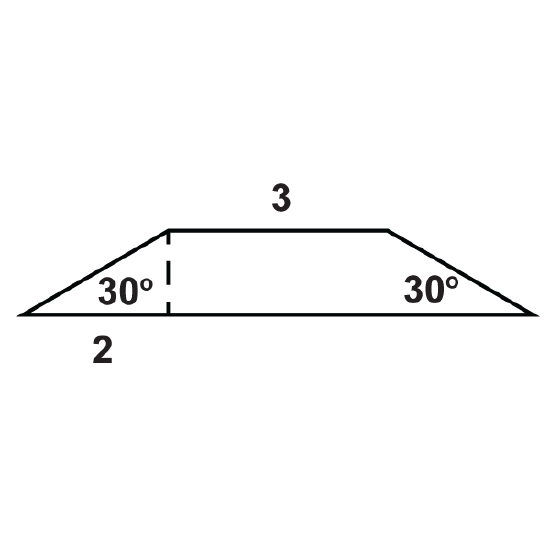
- What is the perimeter of the trapezoid?
- What is the area of the trapezoid?
Review (Answers)
To see the Review answers, open this PDF file and look for section 10.5.
Vocabulary
| Term | Definition |
|---|---|
| area | The amount of space inside a figure. Area is measured in square units. |
| isosceles trapezoid | An isosceles trapezoid is a trapezoid where the non-parallel sides are congruent. |
| midsegment (of a trapezoid) | A line segment that connects the midpoints of the non-parallel sides. |
| perimeter | The distance around a shape. The perimeter of any figure must have a unit of measurement attached to it. If no specific units are given (feet, inches, centimeters, etc), write units. |
| trapezoid | A quadrilateral with exactly one pair of parallel sides. |
Additional Resources
Interactive Element
Video: Area and Perimeter of Trapezoids Examples - Basic
Activities: Area and Perimeter of Trapezoids Discussion Questions
Study Aids: Triangles and Quadrilaterals Study Guide
Practice: Area and Perimeter of Trapezoids
Real World: Perimeter