7.5: Indirect Measurement
- Page ID
- 2158
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Find lengths using proportions of similar triangles.
Unknown Measures of Similar Figures

Shelby's father is a former Olympic swimmer. He loves swimming, but he cannot build an Olympic sized swimming pool in his backyard because he does not have the space. He decides to build a smaller pool that is similar to the dimensions of an Olympic pool. An Olympic pool has a length of 50 meters and a width of 25 meters. His pool has a length of 25 meters. What is the width of his pool?
In this concept, you will learn how to find the unknown measures of similar figures.
Finding Unknown Measures of Similar Figures
If you know the length of a side in one figure, you can use the scale factor to find the measure of the corresponding side in a similar figure. Let’s see how this works.
Side a in triangle ABC corresponds to side x in the smaller triangle XYZ. Side x is 4 meters long and the scale factor is 6. What is the measure of side a?
You have been told that two sides, a and x, correspond in a small triangle and a large one. Side x is 4 meters long, and the scale factor tells you that side a will be six times longer. Let’s write this out and solve.
\(\text{side} x \times \text{ scale factor }=\text{ side }\: a\)
\(4\times 6=\text{ side a }\)
\(24 \text{ m }=\text{ side a }\)
Side a must have a length of 24 meters.
You can check by setting up a ratio that compares the lengths of the two sides. If the scale factor is 6, then your work is accurate.
\(\dfrac{a}{x}=\dfrac{24}{4}=6\)
Sometimes, you can figure out missing side lengths by looking at the given measures. Always look at the diagram of the figures and see if you can determine the missing length without measuring.
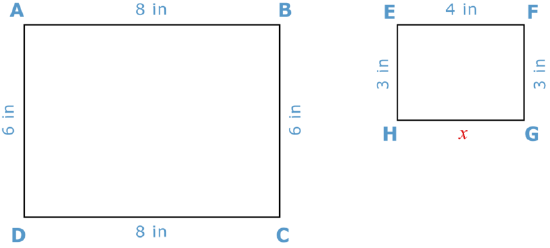
Look at these two rectangles. First, look and see if you can figure out the relationship between the two figures. To do this, you compare the side lengths of each part of the two figures.
You need to figure out the measurement of side GH in the second rectangle.
You can see that the measurements in the second rectangle are half as big as the measurements in the first. Also, you know that the opposite sides of a rectangle are congruent. Therefore, the missing side length is 4.
Similar figures that are related by a scale factor are often seen in maps, architectural blueprints and diagrams. In most of these cases, the scale factor is given so that you know how to enlarge the items in the drawing to their real sizes. Take a look at the floor plan below. It shows where the furniture is located in a living room.
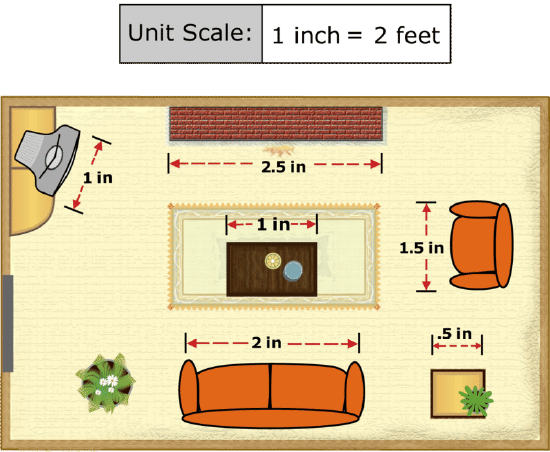
It tells you that one inch in the drawing is equal to two feet in actual size. Therefore, if you know the size in inches of any object in the floor plan, you can find its actual size in feet. Let’s give it a try.
Find the sofa on the floor plan then find its length in inches. The sofa in the floor plan is 2 inches long. This is like knowing the length of one side in a similar figure. Now use the scale factor as you would to find the length of the corresponding side in a similar figure (in this case the “corresponding side” is the actual sofa). Simply multiply the length you know by the scale factor:
\(\text{ sofa drawing }\times \text{ scale factor }=\text{ actual sofa size }\)
\(2\text{ inches }\times 2=4 \text{ feet }\)
The sofa is 4 feet long.
Next, let's calculate the real length of the fireplace.Use a ruler to measure the fireplace in the drawing. It is 2.5 inches long. Multiply this by the scale factor to find the length in feet.
\(\text{ fireplace drawing }\times \text{ scale factor }=\text{ actual fireplace length }\)
\(2.5\text{ inches}\times 2=5 \text{ feet }\)
The real length of the fireplace is 5 feet.
You can also reverse the process to take an actual size and reduce it.
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Shelby's father and his swimming pool.
He builds a pool that is similar to an Olympic pool. An Olympic pool has a length of 50 meters and a width of 25 meters. If his pool has a length of 25 meters, what is the width of his pool?
Solution
First, set up an equation that can be used to solve for the width of his pool.
\(\dfrac{50}{25}=\dfrac{25}{x}\)
Next, cross multiply.
\(50x=625\)
Then, divide both sides of the equation by 50.
\(x= 12.5\)
The answer is that his pool has a width of 12.5 meters.
Example \(\PageIndex{2}\)
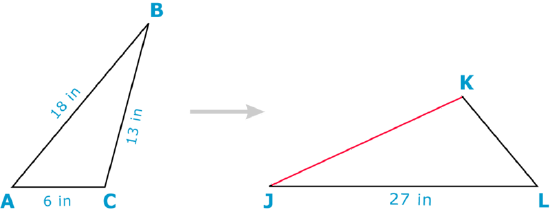
Use the scale factor of the similar figures below to find the measure of KJ.
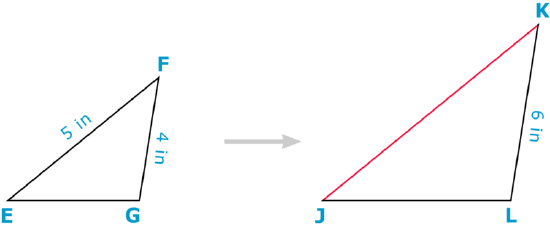
Solution
First, set up a proportion to solve for the missing side.
\(\dfrac{KJ}{5}=\dfrac{6}{4}\)
This proportion is written so that the corresponding sides form the two ratios of the proportion. You can say that \(KJ\) is the unknown in this proportion.
Next, cross multiply.
\(\begin{aligned} KJ\times 4&=4KJ \\ 5\times 6&=30 \\ 4KJ&=30\end{aligned}\)
Then solve the equation for KJ by dividing both sides of the equation by 4.
\(\begin{aligned} 30\divide 4&=7.5 \\ KJ&=7.5 \end{aligned}\)
The answer is that the side length of \(KJ\) is 7.5.
Example \(\PageIndex{3}\)
Chris is making a drawing of his school and the grounds around it. The basketball court is 75 feet long and 40 feet wide. If Chris uses a scale factor in which 1 inch equals 10 feet, what should the dimensions of the basketball court be in his drawing?

Solution
First, write the information that you know.
The actual size of the basketball court and the scale factor Chris is using for his drawing.
Next, set up an equation to find the length Chris should draw.
\(\begin{aligned} \text{ drawing length }\times \text{ scale factor }=\text{ actual basketball court length } \\ \text{ drawing length } \times 10=75 feet \\ \text{ drawing length }&=75\divide 10 \\ \text{ drawing length }&=7.5 \text{ inches }\end{aligned}\)
The length of the basketball court in Chris’s drawing should be 7.5 inches.
Then, use the same process to find the width Chris should draw.
\(\begin{aligned} \text{ drawing width } \times \text{ scale factor }=\text{ actual basketball court width }\\ \text{ drawing width } \times 10=40 \text{ feet } \\ \text{ drawing width }=40\divide 10 \\ \text{ drawing width }=4\text{ inches } \end{aligned}\)
The answer is that Chris should represent the basketball court as a 7.5 by 4 inch rectangle on his drawing.
Example \(\PageIndex{4}\)
Solve for \(x\).
\(\dfrac{3}{4}=\dfrac{x}{12}\)
Solution
First, cross multiply.
\(4x = 36\)
Next, divide both sides of the equation by 4.
\(x = 9\)
Then, state the solution.
9
The answer is that \(x\) equals 9.
Example \(\PageIndex{5}\)
Solve for \(x\).
\(\dfrac{3}{6}=\dfrac{1}{x}\)
Solution
First, cross multiply.
\(3x = 6\)
Next, divide both sides of the equation by 3.
\(x = 2\)
Then, state the solution.
2
The answer is that \(x\) equals 2.
Review
Solve each problem.
- Side \(m\) in triangle \(LMN\) corresponds to side c in the smaller triangle \(BCD\). Side m is 12 cm long and the scale factor is 4. What is the measure of side c?
- Side \(q\) in triangle \(PQR\) corresponds to side y in the smaller triangle \(XYZ\). Side y is 8 inches long and the scale factor is 7. What is the measure of side q?
Solve each proportion for the missing side length.
- \(\dfrac{7}{10}=\dfrac{x}{30}\)
- \(\dfrac{1.5}{3}=\dfrac{x}{6}\)
Now use the scale factor to create a new ratio.
- \(\dfrac{1}{3}\), scale factor 4
- \(\dfrac{8}{5}\), scale factor 5
- \(\dfrac{9}{3}\), scale factor 3
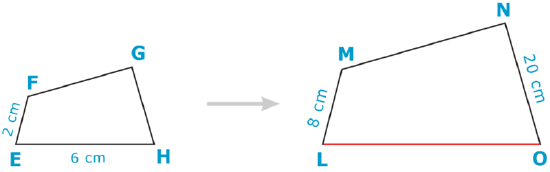
- Find the scale factor of the similar figures below and then use it to find the measure of LO\).
- Use the scale factor of the similar figures below to find the measure of \(JK\).
Use the map below and a ruler to answer the questions that follow.
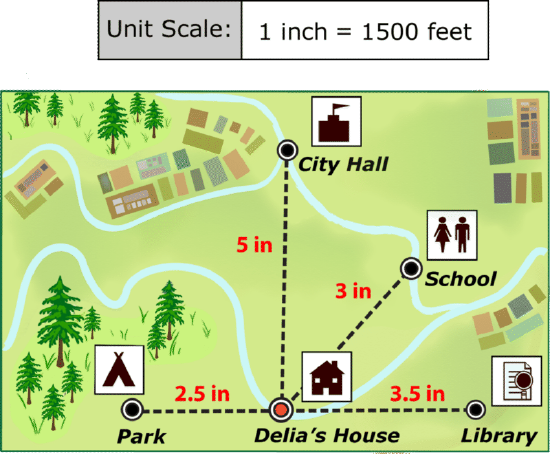
- How far does Delia live from her school?
- How far is it from the library to the park?
- How far does Delia live from City Hall?
- Delia drew another point to show the police station on her map. She drew it 1.5 inches away from the City Hall. What is the actual distance between the police station and City Hall?
- How far does Delia live from the park?
- How far does she live from the library?
- What is the farthest that Delia will travel to any one item on her map?
Review (Answers)
To see the Review answers, open this PDF file and look for section 8.15.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Indirect Measurement | Indirect measurement is the process of using the characteristics of similar triangles to measure distances. |
| Scale Factor | A scale factor is a ratio of the scale to the original or actual dimension written in simplest form. |
| Similar | Two figures are similar if they have the same shape, but not necessarily the same size. |
Additional Resources
Interactive Element
Video: Congruent and Similar Triangles
Practice: Indirect Measurement
Real World: Mighty Measurements

