7.2: Ratio and Proportion in Similar Figures
- Page ID
- 2156
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Simplify ways to compare two numbers.
Proportions
A proportion is two ratios that are set equal to each other. Usually the ratios in proportions are written in fraction form. An example of a proportion is \(\dfrac{2}{x}=510\). To solve a proportion, you need to cross-multiply. The Cross-Multiplication Theorem, which allows us to solve proportions using this method, states that if \(a\), \(b\), \(c\), and \(d\) are real numbers, with \(b\neq 0\) and \(d\neq 0\) and if \(\dfrac{a}{b}=\dfrac{c}{d}\), then \(\dfrac{a}{d}=\dfrac{b}{c}\). Cross-multiplying allows us to get rid of the fractions in our equation. The Cross-Multiplication Theorem has several sub-theorems, called corollaries.
Corollary #1: If \(a\), \(b\), \(c\), and \(d\) are nonzero and \(\dfrac{a}{b}=\dfrac{c}{d}\), then \(\dfrac{a}{c}=\dfrac{b}{d}\).
Switch \(b\) and \(c\).
Corollary #2: If \(a\), \(b\), \(c\), and \(d\) are nonzero and \(\dfrac{a}{b}=\dfrac{c}{d}\), then \(\dfrac{d}{b}=\dfrac{c}{a}\).
Switch \(a\) and \(d\).
Corollary #3: If \(a\), \(b\), \(c\), and \(d\) are nonzero and \(\dfrac{a}{b}=\dfrac{c}{d}\)\), then \(\dfrac{b}{a}=\dfrac{c}{d}\).
Flip each ratio upside down.
Corollary #4: If \(a\), \(b\), \(c\), and \(d\) are nonzero and \dfrac{a}{b}=\dfrac{c}{d}\), then \(\dfrac{a+b}{b}=\dfrac{c+d}{d}\).
Corollary #5: If \(a\), \(b\), \(c\), and \(d\) are nonzero and \(\dfrac{a}{b}=\dfrac{c}{d}\), then \(\dfrac{a−b}{b}=\dfrac{c−d}{d}\).
What if you were told that a scale model of a python is in the ratio of 1:24? If the model measures 0.75 feet long, how long is the real python?
Example \(\PageIndex{1}\)
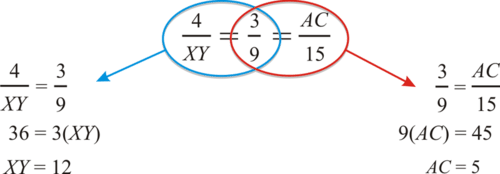
In the picture, \(\dfrac{AB}{XY}=\dfrac{BC}{YZ}=\dfrac{AC}{XZ}\).
Find the measures of \(AC\) and \(XY\).
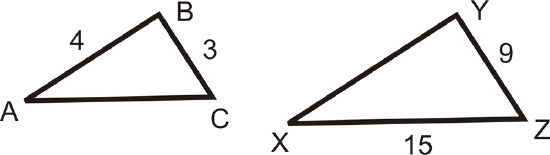
Solution
Plug in the lengths of the sides we know.
Example \(\PageIndex{2}\)
In the picture, \(\dfrac{AB}{BE}=\dfrac{AC}{CD}\). Find \(BE\).
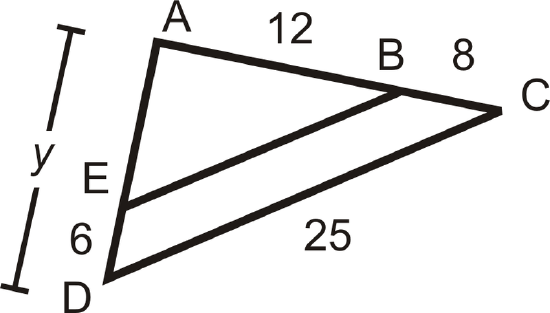
Solution
Substitute in the lengths of the sides we know.
\(\begin{aligned} \dfrac{12}{BE}=\dfrac{20}{25} \rightarrow 20(BE)&=12(25)\\ BE&=15\end{aligned}\)
Example \(\PageIndex{3}\)
Solve the proportions. Remember, to solve a proportion, you need to cross-multiply.
- \(\dfrac{4}{5}=\dfrac{x}{30}\)
- \(\dfrac{y+1}{8}=\dfrac{5}{20}\)
- \(\dfrac{6}{5}=\dfrac{2x+4}{x−2}\)
Solution
-
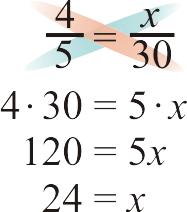
Figure \(\PageIndex{4}\) -
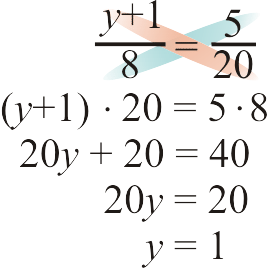
Figure \(\PageIndex{5}\) -
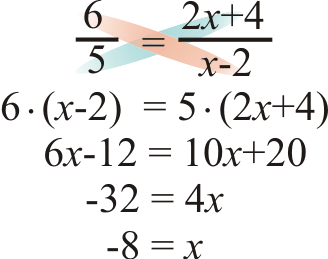
Figure \(\PageIndex{6}\)
Example \(\PageIndex{4}\)
Your parents have an architect’s drawing of their home. On the paper, the house’s dimensions are 36 in by 30 in. If the shorter length of the house is actually 50 feet, what is the longer length?
Solution
To solve, first set up a proportion. If the shorter length is 50 feet, then it lines up with 30 in, the shorter length of the paper dimensions.
\(\begin{aligned}\dfrac{30}{3}6=\dfrac{50}{x} \rightarrow 30x&=1800 \\ x&=60 \qquad \text{The longer length is 60 feet.}\end{aligned}\)
Example \(\PageIndex{5}\)
Suppose we have the proportion \(\dfrac{2}{5}=\dfrac{14}{35}\). Write three true proportions that follow.
Solution
First of all, we know this is a true proportion because you would multiply \(\dfrac{2}{5}\) by \(\dfrac{7}{7}\) to get \(\dfrac{14}{35}\). Using the first three corollaries:
- \(\dfrac{2}{14}=\dfrac{5}{35}\)
- \(\dfrac{35}{5}=\dfrac{14}{2}\)
- \(\dfrac{5}{2}=\dfrac{35}{14}\)
Review
Solve each proportion.
- \(\dfrac{x}{10}=\dfrac{42}{35}\)
- \(\dfrac{x}{x−2}=\dfrac{5}{7}\)
- \(\dfrac{6}{9}=\dfrac{y}{24}\)
- \(\dfrac{x}{9}=\dfrac{16}{x}\)
- \(\dfrac{y−3}{8}=\dfrac{y+6}{5}\)
- \(\dfrac{20}{z+5}=\dfrac{16}{7}\)
- Shawna drove 245 miles and used 8.2 gallons of gas. At the same rate, if she drove 416 miles, how many gallons of gas will she need? Round to the nearest tenth.
- The president, vice-president, and financial officer of a company divide the profits is a 4:3:2 ratio. If the company made $1,800,000 last year, how much did each person receive?
Given the true proportion, \(\dfrac{10}{6}=\dfrac{15}{d}=\dfrac{x}{y}\) and \(d\), \(x\), and \(y\) are nonzero, determine if the following proportions are also true.
- \(\dfrac{10}{y}=\dfrac{x}{6}\)
- \(\dfrac{15}{10}=\dfrac{d}{6}\)
- \(\dfrac{6+10}{10}=\dfrac{y+x}{x}\)
- \(\dfrac{15}{x}=\dfrac{y}{d}\)
For questions 13-16, \(\dfrac{AE}{ED}=\dfrac{BC}{CD}\) and \(\dfrac{ED}{AD}=\dfrac{CD}{DB}=\dfrac{EC}{AB}\).
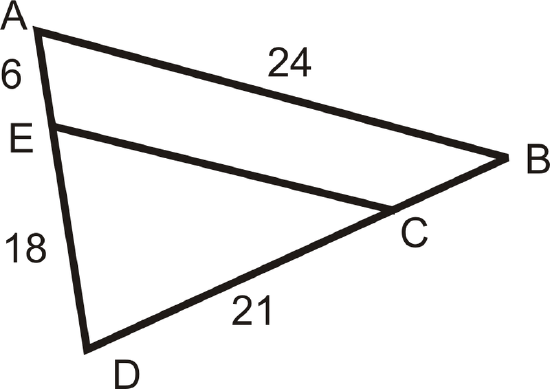
- Find DB.
- Find EC.
- Find CB.
- Find AD.
Resources
Review (Answers)
To see the Review answers, open this PDF file and look for section 7.2.
Vocabulary
| Term | Definition |
|---|---|
| corollary | A theorem that follows directly from another theorem. |
| proportion | Two ratios that are set equal to each other. |
| ratio | A way to compare two numbers. Ratios can be written in three ways: \dfrac{a}{b}, a:b, and a to b. |
| Cross Products | To simplify a proportion using cross products, multiply the diagonals of each ratio. |
| Cross-Multiplication Theorem | The Cross-Multiplication theorem states that if \(a\), \(b\), \(c\) and \(d\) are real numbers, with \(b\neq 0\) and \(d\neq 0\) and if \(\dfrac{a}{b}=\dfrac{c}{d}\), then \(\dfrac{a}{d}=\dfrac{b}{c}\). |
Additional Resources
Interactive Element
Video: Ratios
Activities: Forms of Ratios Discussion Questions
Study Aids: Ratios and Proportions Study Guide
Practice: Ratio and Proportion in Similar Figures
Real World: In the Doll's House

