7.1: Similar Figures
- Page ID
- 2154
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Figures that have the same shape but not the same size.
Triangle Identification as Similar, Congruent, or Neither
Gabriel is in geometry. He uses different tools to measure different items. One day he sits a couple of his tools together and he notices that two of his tools are triangles. His class has recently compared triangles and identified them as similar, congruent or neither. The class is supposed to be using their measuring tools to measure items around the classroom and determine if they are similar, congruent or neither. Gabriel takes a good look at the two shapes then decides to identify them so that he can add them to his list. Are Gabriel's triangles similar, congruent or neither?
In this concept, you will learn to distinguish between triangles.
Identifying Triangles as Similar, Congruent, or Neither
Congruent means being exactly the same. When two line segments have the same length, they are congruent. When two figures have the same shape and size, they are congruent.
These two triangles are congruent. They are exactly the same in every way. They are the same size and the same shape. Their side lengths are the same and that their angle measures are the same.
Sometimes, two figures will be similar. Similar means that the figures have the same shape, but not the same size. Similar figures are not congruent.
These two triangles are similar. They are the same shape, but they are not the same size.
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Gabriel and his measuring tools.
He notices that two of his tools are triangles. Are his triangles similar, congruent or neither?
Solution
First, check to see if the triangles are the same size.
No
Next, check to see if the triangles are the same shape.
No
Then, identify the triangles.
The answer is that the triangles are neither similar, nor congruent. Gabriel will list the triangles as neither.
Example \(\PageIndex{2}\)
Identify the following triangles as similar, congruent or neither.
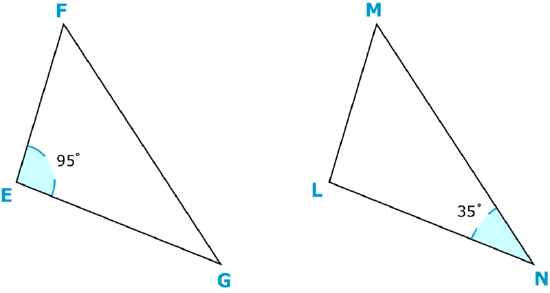
Solution
First, check to see if the triangles have the same size.
Yes
Next, check to see if the triangles have the same shape.
Yes
Then, identify the triangles.
Congruent
The answer is that the triangles are congruent.
Example \(\PageIndex{3}\)
Identify the following triangles as similar, congruent, or neither.
Solution
First, check to see if the triangles are the same size.
No
Next, check to see if the triangles are the same shape.
No
Then, identify the triangles.
Neither congruent, nor similar
The answer is that the triangles are neither congruent, nor similar.
Example \(\PageIndex{4}\)
Identify the following triangles as similar, congruent, or neither.
Solution
First, check to see if the triangles are the same size.
No
Next, check to see if the triangles are the same shape.
Yes
Then, identify the triangles.
Similar
The answer is that the triangles are similar.
Example \(\PageIndex{5}\)
Identify the following triangles as similar, congruent, or neither.
Solution
First, check to see if the triangles are the same size.
Yes
Next, check to see if the triangles are the same shape.
Yes
Then, identify the triangles.
Congruent
The answer is that the triangles are congruent.
Review
Identify the given triangles as visually similar, congruent or neither.
-
Figure \(\PageIndex{8}\) -
Figure \(\PageIndex{9}\) -
Figure \(\PageIndex{10}\) -
Figure \(\PageIndex{11}\) -
Figure \(\PageIndex{12}\)
Answer each of the following questions.
- Triangles \(ABC\) and \(DEF\) are congruent. Does this mean that their angle measures are the same? Why?
- True or false. If triangles \(DEF\) and \(GHI\) are similar, then the side lengths are different but the angle measures are the same.
- True or false. Similar figures have exactly the same size and shape.
- True or false. Congruent figures are exactly the same in every way.
- Triangles \(LMN\) and \(HIJ\) are similar. If this is true, then the side lengths are the same, true or false.
- True or false. To figure out if two figures are similar, then their side lengths form a proportion.
- Define similar figures
- Define congruent figures.
- Use a ruler to draw a congruent pair of triangles.
- Use a ruler to draw a pair of triangles that is similar.
Review (Answers)
To see the Review answers, open this PDF file and look for section 9.15.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Congruent | Congruent figures are identical in size, shape and measure. |
| Similar | Two figures are similar if they have the same shape, but not necessarily the same size. |
Additional Resources
Interactive Element
Video: Congruent and Similar Triangles - KA
Practice: Similar Figures