7.4: Corresponding Parts of Similar Figures
- Page ID
- 2157
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Identify matching side lengths and angle measures in similar figures.
Maria has an art project due for school. She decides to make a small replica of her bedroom. She begins by measuring the angles of her bedroom, then she draws similar figures. The larger figure represents her bedroom and the smaller figure represents her replica.
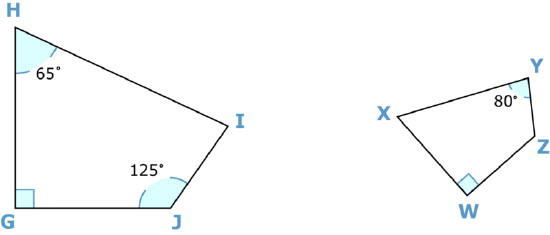
Her bedroom door is located in the middle of \(\overline{IJ}\). For her replica, the door must be placed in the middle of the corresponding side. What side of the replica corresponds to \(\overline{IJ}\)?
In this concept, you will learn about corresponding sides of similar figures.
Corresponding Parts of Similar Figures
Triangle ABC is similar to triangle DEF. This means that while they are the same shape, they aren’t the same size. In fact, there is a relationship between the corresponding parts of the triangle.
The side lengths are corresponding even though they aren’t congruent. Use the symbol for similar ("\(\sim\)") to show the relationship between the corresponding sides of the two triangles.
\(\overline{AB}\sim \overline{DE}\)
\(\overline{BC}\sim \overline{EF}\)
\(\overline{AC}\sim \overline{DF}\)
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Maria and her bedroom.
She is making a replica of her bedroom for her art class. She draws two similar figures to make sure that she is placing everything in the right position.
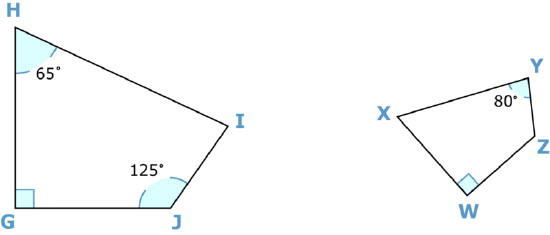
Solution
She needs to place her bedroom door in the middle of the side that corresponds to \(\overline{IJ}\). What side corresponds to \(\overline{IJ}\)?
First, rotate the second figure so that it looks like the first figure.
Then, locate the side on the second figure that is in the position that \(\overline{IJ}\) is in the first figure.
\(\overline{YZ}\)
The answer is that \(\overline{YZ}\) corresponds to \(\overline{IJ}\). Maria needs to place her bedroom door in the middle of \(\overline{YZ}\) on the replica.
Example \(\PageIndex{2}\)
The figures below are similar. What side corresponds \(\overline{NO}\)?
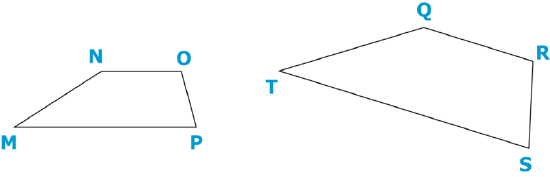Figure \(\PageIndex{5}\)Solution
First, position the second figure so that it looks like the first figure.
Then, identify the side in the second figure that is in the same position as \(\overline{NO}\) is in the first figure.
\(\overline{QR}\)
The answer is that \(\overline{QR}\) corresponds to \(\overline{NO}\).
Example \(\PageIndex{3}\)
\(\overline{AB}\sim _____\)
Solution
First, look to see which side in the second triangle corresponds to the given segment.
\(\overline{EF}\)
Then, complete the problem.
\(\overline{AB}\sim \overline{EF}\)
The answer is that \(\overline{AB}\sim \overline{EF}\).
Example \(\PageIndex{4}\)
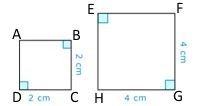
What makes the two squares similar if they both have four right angles?
Solution
First, check to see if the side lengths are the same.
No
Next, check to see if the shape is the same.
Yes
Then, state why the two squares are similar.
Same shape, different sizes
The answer is that the two squares are similar because they have the same shape, but different sizes.
Example \(\PageIndex{5}\)
In the triangle pair, are the two triangles similar or congruent?
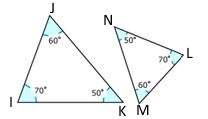Figure \(\PageIndex{8}\)Solution
First, check to see if the two triangles are the same size.
No
Next, check to see if the two triangles are the same shape.
Yes
Then, determine if the two triangles are similar or congruent.
Similar
The two triangles are similar.
Review
Use the following figures to answer each question.
- Are these two triangles similar or congruent?
- How do you know?
- Which side is congruent to \(\overline{AB}\)?
- Which side is congruent to \(\overline{AC}\)?
- Which side is congruent to \(\overline{RS}\)?
- Which angle is congruent to angle A?
- Which angle is congruent to angle B?
- Which angle is congruent to angle C?
- Are the two figures similar or congruent?
- Why?
- Which side is congruent to \(\overline{NO}\)?
- Which side is congruent to \(\overline{MN}\)?
- Which side is congruent to \(\overline{ST}\)?
- Which side is congruent to \(\overline{QT}\)?
- Which side is congruent to \(\overline{OP}\)?
Review (Answers)
To see the Review answers, open this PDF file and look for section 9.17.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Congruent | Congruent figures are identical in size, shape and measure. |
| Corresponding | The corresponding sides between two triangles are sides in the same relative position. |
| Similar | Two figures are similar if they have the same shape, but not necessarily the same size. |
Additional Resources
Video: Congruent and Similar Triangles
Practice: Corresponding Parts of Similar Figures