7.3: Similar Polygons and Scale Factors
- Page ID
- 2159
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Similar Polygons
Similar polygons are two polygons with the same shape, but not the same size. Similar polygons have corresponding angles that are congruent, and corresponding sides that are proportional.
These polygons are not similar:
Scale Factors
Think about similar polygons as enlarging or shrinking the same shape. The symbol \sim\) is used to represent similarity. Specific types of triangles, quadrilaterals, and polygons will always be similar. For example, all equilateral triangles are similar and all squares are similar. If two polygons are similar, we know the lengths of corresponding sides are proportional. In similar polygons, the ratio of one side of a polygon to the corresponding side of the other is called the scale factor. The ratio of all parts of a polygon (including the perimeters, diagonals, medians, midsegments, altitudes) is the same as the ratio of the sides.
What if you were told that two pentagons were similar and you were given the lengths of each pentagon's sides. How could you determine the scale factor of pentagon #1 to pentagon #2?
Example \(\PageIndex{1}\)
\(ABCD\) and \(UVWX\) are below. Are these two rectangles similar?
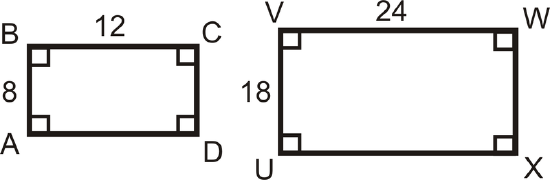
Solution
All the corresponding angles are congruent because the shapes are rectangles.
Let’s see if the sides are proportional. \(\dfrac{8}{12}=\dfrac{2}{3}\) and \(\dfrac{18}{24}=\dfrac{3}{4}\). \(\dfrac{2}{3}\neq \dfrac{3}{4}\), so the sides are not in the same proportion, and the rectangles are not similar.
Example \(\PageIndex{2}\)
\(\Delta ABC\sim \Delta MNP\). The perimeter of \(\Delta ABC\) is 150, \(AB=32\) and \(MN=48\). Find the perimeter of \(\Delta MNP\).
Solution
From the similarity statement, \(AB\) and \(MN\) are corresponding sides. The scale factor is \(\dfrac{32}{48}=\dfrac{2}{3}\) or \(\dfrac{3}{2}\). \Delta ABC\) is the smaller triangle, so the perimeter of \(\Delta MNP\) is \(\dfrac{3}{2}(150)=225\).
Example \(\PageIndex{3}\)
Suppose \(\Delta ABC\sim \Delta JKL\). Based on the similarity statement, which angles are congruent and which sides are proportional?
Solution
Just like in a congruence statement, the congruent angles line up within the similarity statement. So, \(\angle A\cong \angle J\), \(\angle B\cong \angle K\), and \angle C\cong \angle L\). Write the sides in a proportion: \(\dfrac{AB}{JK}=\dfrac{BC}{KL}=\dfrac{AC}{JL}\). Note that the proportion could be written in different ways. For example, \(\dfrac{AB}{BC}=\dfrac{JK}{KL}\) is also true.
Example \(\PageIndex{4}\)
\(MNPQ \sim RSTU\). What are the values of \(x\), \(y\) and \(z\)?
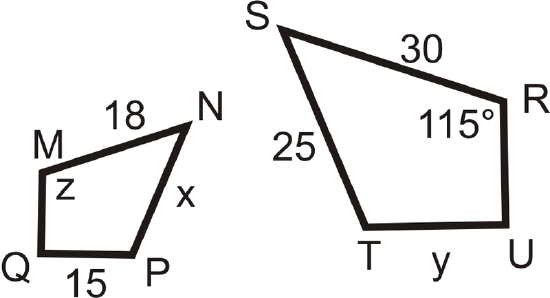
Solution
In the similarity statement, \(\angle M\cong \angle R\), so \(z=115^{\circ}\). For \(x\) and \(y\), set up proportions.
\(\dfrac{18}{30}=\dfrac{x}{25} \qquad \dfrac{18}{30}=\dfrac{15}{y}\)
\(450=30x \qquad 18y=450\)
\(x=15\qquad y=25\)
Example \(\PageIndex{5}\)
\(ABCD\sim AMNP\). Find the scale factor and the length of \(BC\).
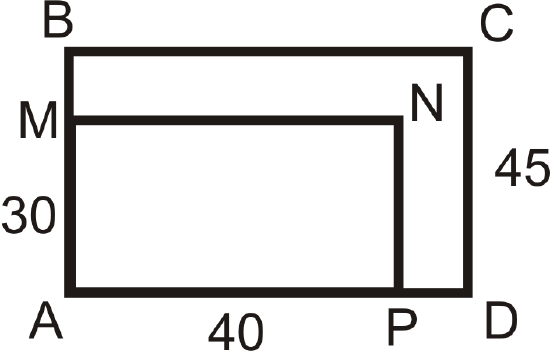
Solution
Line up the corresponding sides, \(AB\) and \(AM=CD\), so the scale factor is \(\dfrac{30}{45}=\dfrac{2}{3}\)or \(\dfrac{3}{2}\). Because \(BC\) is in the bigger rectangle, we will multiply 40 by \(\dfrac{3}{2}\) because \(\dfrac{3}{2}\) is greater than 1. \(BC=\dfrac{3}{2}(40)=60\).
Review
For questions 1-8, determine whether the following statements are true or false.
- All equilateral triangles are similar.
- All isosceles triangles are similar.
- All rectangles are similar.
- All rhombuses are similar.
- All squares are similar.
- All congruent polygons are similar.
- All similar polygons are congruent.
- All regular pentagons are similar.
- \(\Delta BIG \sim \Delta HAT\). List the congruent angles and proportions for the sides.
- If \(BI=9\) and \(HA=15\), find the scale factor.
- If \(BG=21\), find \(HT\).
- If \(AT=45\), find \(IG\).
- Find the perimeter of \(\Delta BIG\) and \(\Delta HAT\). What is the ratio of the perimeters?
- An NBA basketball court is a rectangle that is 94 feet by 50 feet. A high school basketball court is a rectangle that is 84 feet by 50 feet. Are the two rectangles similar?
- HD TVs have sides in a ratio of 16:9. Non-HD TVs have sides in a ratio of 4:3. Are these two ratios equivalent?
Use the picture to the right to answer questions 16-20.
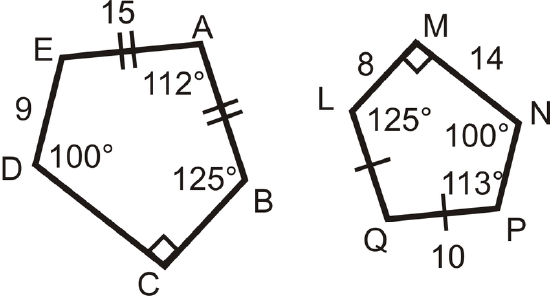
- Find \(m\angle E\) and \(m\angle Q\).
- \(ABCDE\sim QLMNP\), find the scale factor.
- Find BC.
- Find CD.
- Find NP.
Determine if the following triangles and quadrilaterals are similar. If they are, write the similarity statement.
-
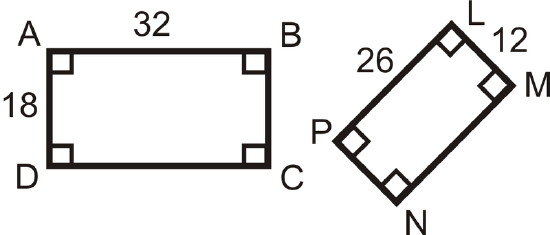
Figure \(\PageIndex{7}\) -
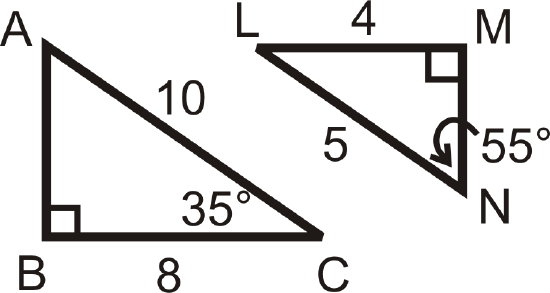
Figure \(\PageIndex{8}\) -
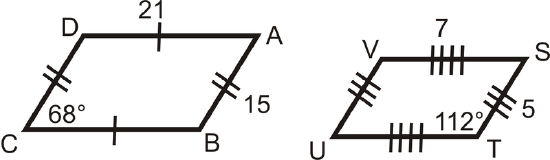
Figure \(\PageIndex{9}\) -
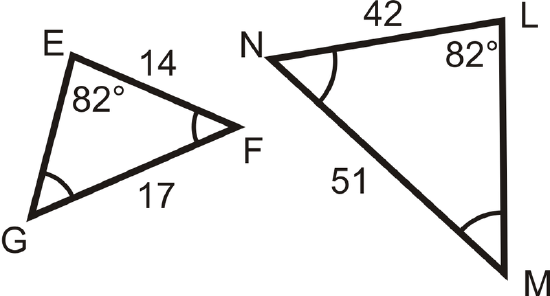
Figure \(\PageIndex{10}\) -
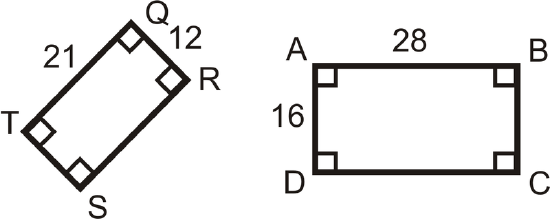
Figure \(\PageIndex{11}\) -
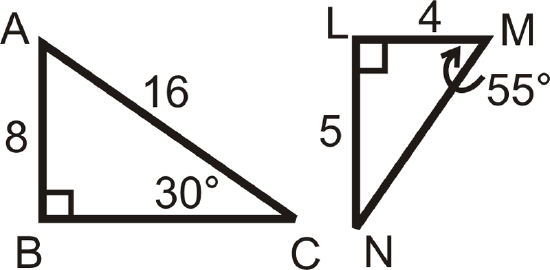
Figure \(\PageIndex{12}\) -
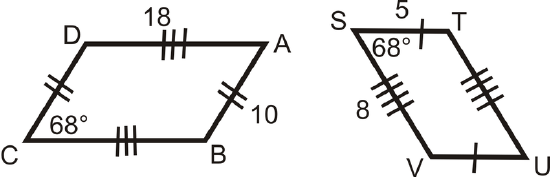
Figure \(\PageIndex{13}\) -
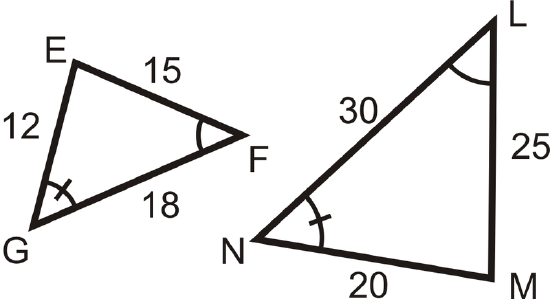Figure \(\PageIndex{14}\) -
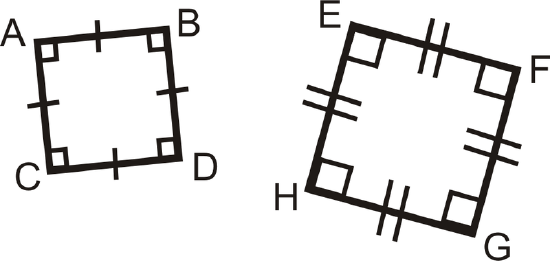
Figure \(\PageIndex{15}\) -
Figure \(\PageIndex{16}\)
Resources
Vocabulary
| Term | Definition |
|---|---|
| similar polygons | Two polygons with the same shape, but not the same size. The corresponding angles of similar polygons are congruent (exactly the same) and the corresponding sides are proportional (in the same ratio). In similar polygons, the ratio of one side of a polygon to the corresponding side of the other is called the scale factor. |
| Congruent | Congruent figures are identical in size, shape and measure. |
| Proportion | A proportion is an equation that shows two equivalent ratios. |
| Scale Factor | A scale factor is a ratio of the scale to the original or actual dimension written in simplest form. |
| sine | The sine of an angle in a right triangle is a value found by dividing the length of the side opposite the given angle by the length of the hypotenuse. |
| Trigonometric Ratios | Ratios that help us to understand the relationships between sides and angles of right triangles. |