9.5: Volume
- Page ID
- 2171
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Number of unit cubes to fill prisms, spheres, pyramids, cylinders, cones, and composite solids.
Volume of Solids
The volume of a solid is the measure of how much space an object takes up. It is measured by the number of unit cubes it takes to fill up the solid.

Volume of a Prism
A prism is a solid with two congruent polygon bases that are parallel and connected by rectangles. Prisms are named by their base shape.
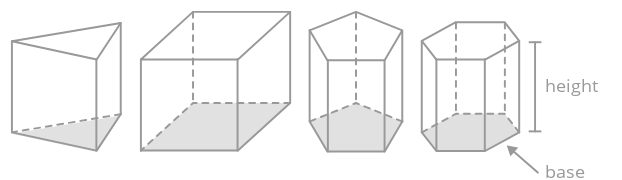
To find the volume of a prism, find the area of its base and multiply by its height.
\(V_{prism}=A_{base}\cdot h\)
Volume of a Cylinder
A cylinder is a three-dimensional solid consisting of two congruent, parallel, circular sides (the bases), joined by a curved surface.
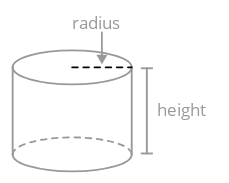
To find the volume of a cylinder, find the area of its circular base and multiply by its height.
\(V_{cylinder}= \pir^{2}h\)
CK-12 PLIX: Surface Area and Volume of Cylinders
Interactive Element
Volume of a Pyramid
A pyramid is a three dimensional solid with a polygonal base. Each corner of a polygon is attached to a singular vertex, which gives the pyramid its distinctive shape. Each base edge and the vertex form a triangle. Pyramids are named by their base shape.
To find the volume of a pyramid, find the volume of the prism with the same base and divide by three.
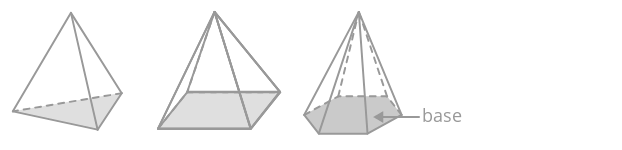
\(V_{pyramid}=\dfrac{A_{base}\cdot h}{3}\)
Volume of a Cone
A cone is a three-dimensional solid with a circular base whose lateral surface meets at a point called the vertex.
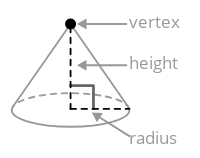
To find the volume of a cone, find the volume of the cylinder with the same base and divide by three.
\(V_{cone}=\dfrac{ \pi r^{2}h}{3}\)
Consider:
What is the ratio between the volume of a cylinder and of a cone, having the same radius and height?
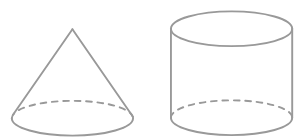
The ratio between the volume of a cylinder and a cone with the same radius and height is _______.
Volume of a Sphere
A sphere is the set of all points in space equidistant from a center point. The distance from the center point to the sphere is called the radius.
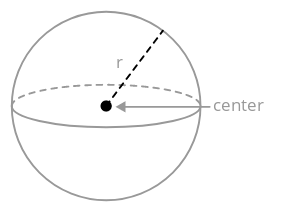
The volume of a sphere relies on its radius.
\(V_{sphere}=\dfrac{4}{3} \pi r^{3}\)
Calculating Volume
Click the small blue arrow next to the image below and drag the orange dots to adjust the dimensions of the solid given below and observe how the volume changes.

Figure \(\PageIndex{8}\)
Volume of a Composite Solid
A composite solid is a solid made up of common geometric solids. The solids that it is made up of are generally prisms, pyramids, cones, cylinders and spheres.
The volume of a composite solid is the sum of the volumes of the individual solids that make up the composite.
Let's look at some problems where we find the volume.
1. Find the volume of the rectangular prism below.
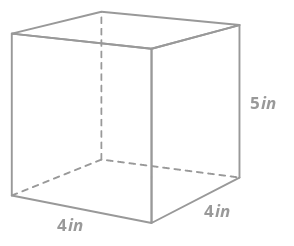
To find the volume of the prism, you need to find the area of the base and multiply by the height. Note that for a rectangular prism, any face can be the “base”, not just the face that appears to be on the bottom.

2. Find the volume of the cone below.
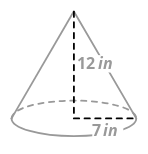
To find the volume of the cone, you need to find the area of the circular base, multiply by the height, and divide by three.

3. Find the volume of a sphere with radius 4 cm.
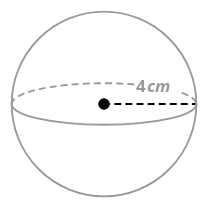
\(\begin{aligned} \text{Volume of Sphere }&=&\dfrac{4}{3} \pi r^{3} \\ &=&\dfrac{4}{3} \pi(4)^{3} \\ &=&\dfrac{256 \pi}{3} cm^{3}\end{aligned}\)
Example \(\PageIndex{1}\)
The composite solid below is made of a cube and a square pyramid. The length of each edge of the cube is 12 feet and the overall height of the solid is 22 feet. What is the volume of the solid? Why might you want to know the volume of the solid?
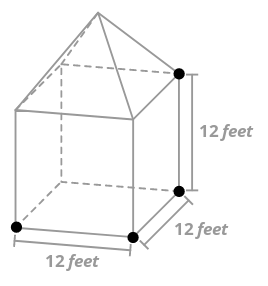
Solution
To find the volume of the solid, find the sum of the volumes of the prism (the cube) and the pyramid. Note that since the overall height is 22 feet and the height of the cube is 12 feet, the height of the pyramid must be 10 feet.
\(\begin{aligned}
\text { Volume of Prism (Cube) } &=A_{\text {base }} \cdot h \\
&=(12 \cdot 12)(12) \\
&=1728 \mathrm{ft}^{3} \\
\text { Volume of Pyramid } &=\frac{A_{\text {base }} \cdot h}{3} \\
&=\frac{(12 \cdot 12)(10)}{3} \\
&=480 \mathrm{ft}^{3} \\
&=\text { Volume of Prism (Cube) }+\text { Volume of Pyramid } \\
&=1728+480 \\
&=2208 \mathrm{ft}^{3}
\end{aligned}\)
The volume helps you to know how much the solid will hold. One cubic foot holds about 7.48 gallons of liquid, so
\(\begin{aligned}
\text { Gallons of liquid the solid can hold } &=\text { Volume of solid . Number of gallons/cubic foot } \\
&=(2208)(7.48) \\
&=16,515.84 \text { gallons }
\end{aligned}\)
Example \(\PageIndex{2}\)
The area of the base of the pyramid below is \(100 cm^{2}\). The height is 5 cm. What is the volume of the pyramid?
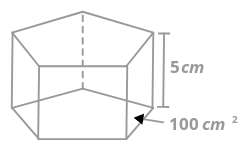
Solution
\(V_{prism}=A_{base}\cdot h=(100\text{ cm}^{2} )\cdot (5 cm)=500\text{ cm}^{3}\)
Example \(\PageIndex{3}\)
The volume of a sphere is \(\dfrac{500 \pi}{3} in^{3}\). What is the radius of the sphere?
Solution
To find the radius, use the formula: \(Volume\: of\: Sphere = \dfrac{4}{3} \pir^{3}\)
\(\begin{aligned} \dfrac{500 \pi}{3}&=\dfrac{4}{3} \pi r^{3} \\ 4r^{3} =500 \\ r^{3} &=125 \\ r&=5\text{ in} \end{aligned}\)
Example \(\PageIndex{4}\)
The volume of a square pyramid is \(64 in^{3}\). The height of the pyramid is three times the length of a side of the base. What is the height of the pyramid?
Solution

Side \(s=4\) in and height \(h=3(4)=12 in.\)
Review
Find the volume of each solid or composite solid.
-
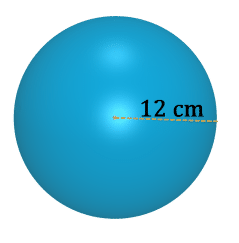
Figure \(\PageIndex{14}\) -
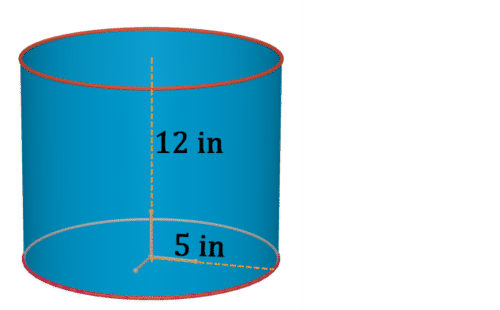
Figure \(\PageIndex{15}\) -
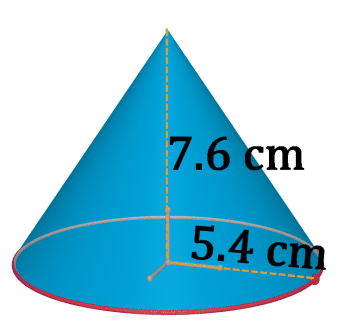
Figure \(\PageIndex{16}\) -
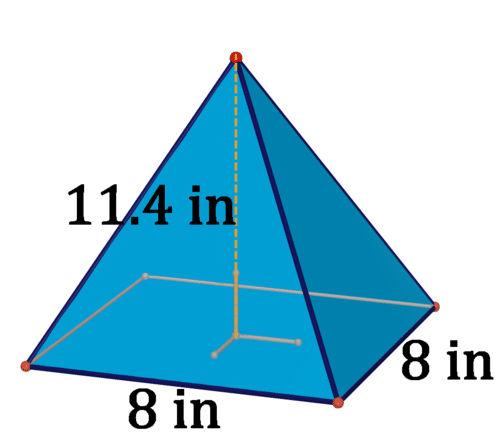
Figure \(\PageIndex{17}\) - The base is an equilateral triangle.
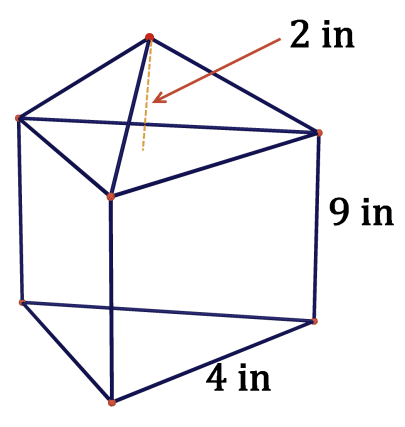
Figure \(\PageIndex{18}\) -
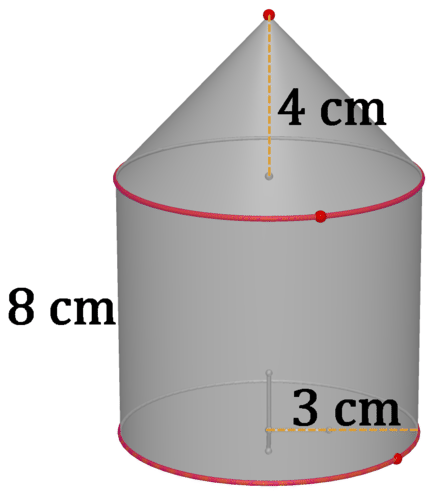
Figure \(\PageIndex{19}\)
7. Explain why the formula for the volume of a prism involves the area of the base.
8. How is a cylinder related to a prism?
9. How is a pyramid related to a cone?
10. How is a sphere related to a circle?
11. If one cubic centimeter will hold 1 milliliter of water, approximately how many liters of water will the solid in #1 hold? (One liter is 1000 milliliters).
12. If one cubic centimeter will hold 1 milliliter of water, approximately how many liters of water will the solid in #3 hold? (One liter is 1000 milliliters).
13. If 231 cubic inches will hold one gallon of water, approximately how many gallons of water will the solid in #5 hold?
14. The volume of a cone is \(125 \pi in^3\). The height is three times the length of the radius. What is the height of the cone?
15. The volume of a pentagonal prism is \(360 in^3\). The height of the prism is 3 in. What is the area of the pentagon base?
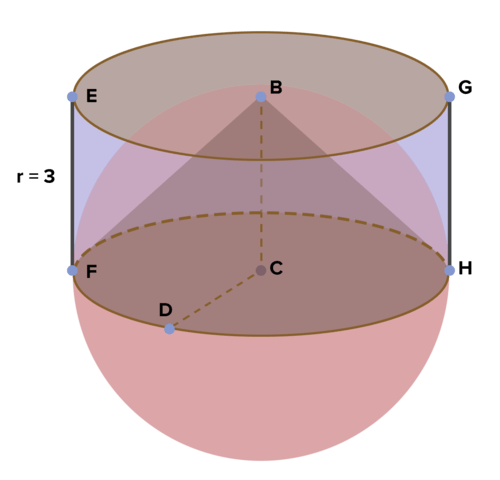
16. The figure below features a cylinder whose height is 3 units. Inside the cylinder is a hemisphere (half of a sphere). And inside the hemisphere is a cone. Find the volume of the cylinder and the cone. Find the volume of the sphere and then the hemisphere. Do you see a relationship between the volume of the cylinder and cone, and that of the hemisphere? Explain. Use this to derive the formula for volume of a sphere from the formulas for a cylinder and cone.
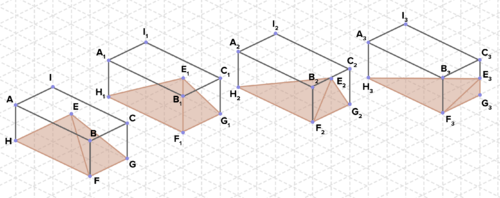
17. The isometric grid below is composed of equilateral triangles whose side are of unit length 1. Find the volume for each of the pyramids. What do you observe? Explain.
18. Find the surface area and volume of the following pyramid. Each line segment in the background grid is length 1.
Review (Answers)
To see the Review answers, click here.

