9.6: Cross Sections and Basic Solids of Revolution
- Page ID
- 2172
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Cross sections of solids and solids created by rotating shapes around lines.
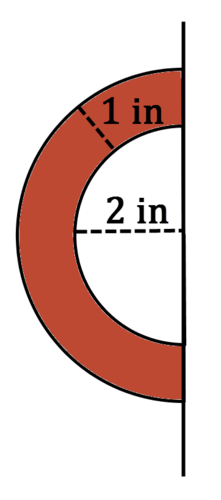
The shaded figure below is rotated around the line. What is the volume of the solid that is created?
Cross Sections
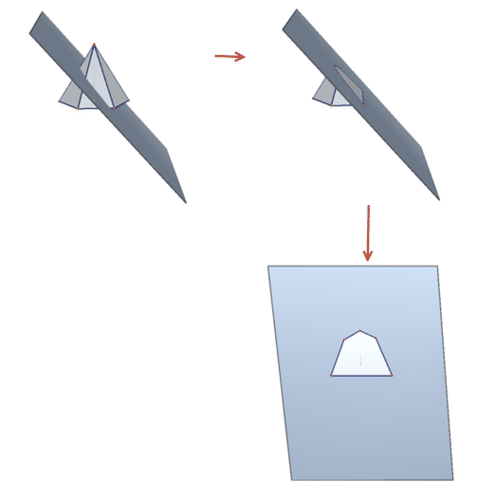
Recall that a cross section is the shape you see when you make one slice through a solid. A solid can have many different cross sections depending on where you make the slice. Consider a hexagonal pyramid. Cross sections perpendicular to the base will be triangles. Cross sections parallel to the base will be hexagons. It is also possible to take cross sections using planes that are neither parallel nor perpendicular to the base. Below, a hexagonal pyramid has been sliced at a slant. The cross section is a pentagon.
Interactive Element
Add interactive element text here. This box will NOT print up in pdfs
Cross sections are one way that two dimensional objects are connected to three dimensional objects.
A second connection between two and three dimensions comes from the fact that three dimensional solids can be created by rotating two dimensional objects around a line.
Interactive Element
Add interactive element text here. This box will NOT print up in pdfs
Let's look at some problems about cross sections.
- Identify the solid that is created when the following shape is rotated around the line.
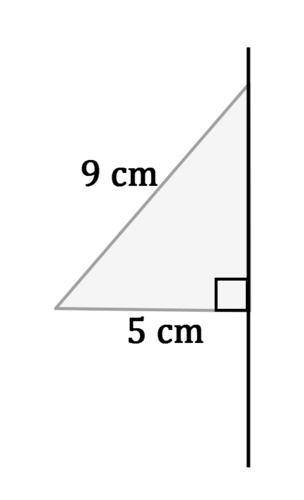
The solid is a cone with radius 5 cm.
- Find the volume of the solid from #1.
The volume of a cone is \(V=\dfrac{\pi r^{2}h}{3}\). The radius is 5 cm. To find the height of the cone, use the Pythagorean Theorem:
\(5^{2}+h^{2}=9^{2}\)
\(h=\sqrt{56}\approx 7.48\: cm\)
The volume of the cone is:
\(V=\dfrac{\pi (5^{2})(7.48)}3\approx 195.83 cm^{3}\)
- Identify at least three two dimensional shapes created by cross sections of the solid from first problem.
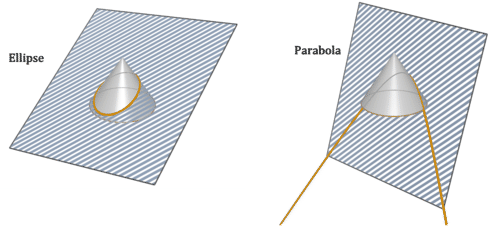
Cross sections taken parallel to the base will be circles. Cross sections taken perpendicular to the base will be triangles. When the cross section is taken at a slant, there are many other possibilities. Two additional cross sections are an ellipse or a filled in parabola.
Example \(\PageIndex{1}\)
Earlier, you were asked what is the volume of the solid that was created.
The shaded figure below is rotated around the line.

Solution
The resulting solid is a sphere with a sphere removed from the center. The volume of the large sphere is \(\dfrac{4\pi (3^{3})}{3}=36\pi in^{3}\). The volume of the small sphere is \(\dfrac{4\pi (2^{3})}{3}=32\pi 3 in^{3}\). The volume of the resulting solid is:
\(V=36\pi −\dfrac{32\pi} {3}=\dfrac{76\pi}{3}\text{ in}^{3}\)
Use the picture below for #2-#4.
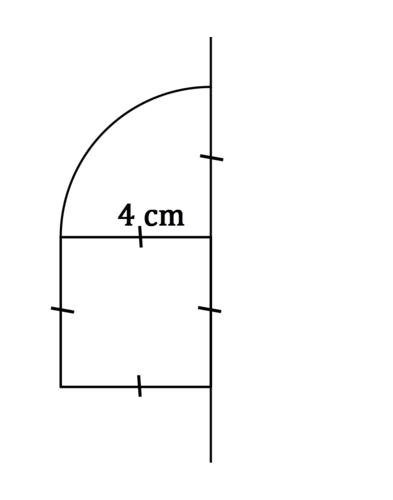
Example \(\PageIndex{2}\)
Identify the solid that is created when the figure above is rotated around the line.
Solution
The solid is a cylinder with a hemisphere on top. The radius of each is 4 cm.
Example \(\PageIndex{3}\)
Find the volume of the solid from #2.
Solution
The volume of the cylinder is \(\pi (4^{2})(4)=64\pi cm^{3}\). The volume of the hemisphere is \(\dfrac{4\pi (4^{3})}{6}=\dfrac{128\pi}{3} cm^{3}\). The volume of the whole solid is \(\dfrac{320\pi}{3} cm^{3}\).
Example \(\PageIndex{4}\)
Identify at least three two dimensional shapes created by cross sections of the solid from #2.
Solution
Possible answers: Cross sections taken parallel to the base will be circles. Cross sections taken perpendicular to the base will be rectangles with half circles on top. Some cross sections taken at a slant will be ellipses.
Review
Use the picture below for #1-#3.
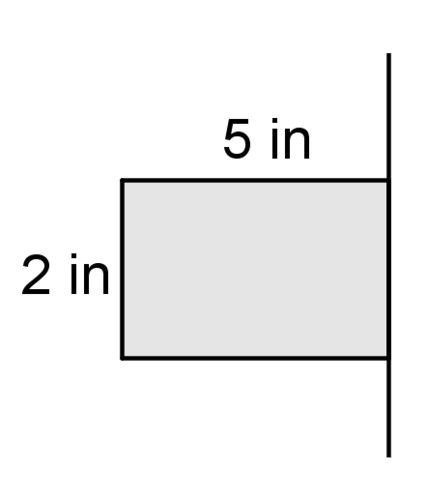
1. Describe the solid that is created when the figure above is rotated around the line.
2. Find the volume of the solid.
3. Identify at least 3 two dimensional shapes created by cross sections of the solid.
Use the picture below for #4-#6.
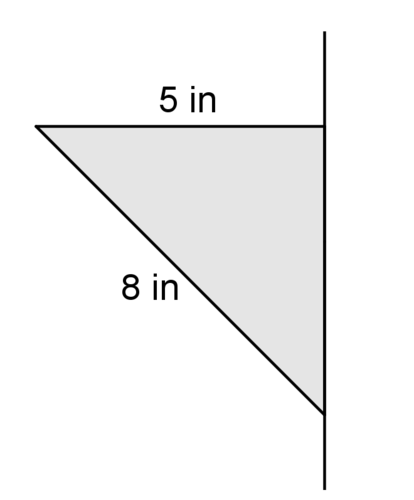
4. Describe the solid that is created when the figure above is rotated around the line.
5. Find the volume of the solid.
6. Identify at least 3 two dimensional shapes created by cross sections of the solid.
Use the picture below for #7-#9.
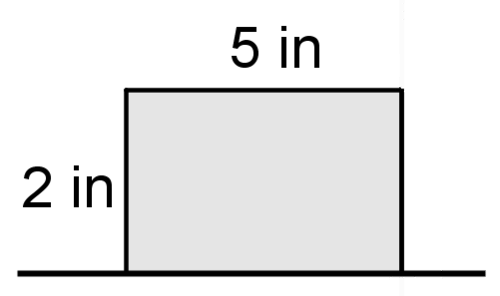
7. Describe the solid that is created when the figure above is rotated around the line.
8. Find the volume of the solid.
9. Identify at least 2 two dimensional shapes created by cross sections of the solid.
Use the picture below for #10-#12.
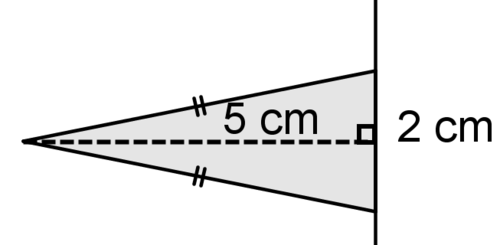
10. Describe the solid that is created when the figure above is rotated around the line.
11. Find the volume of the solid.
12. Identify at least 2 two dimensional shapes created by cross sections of the solid.
Use the picture below for #13-#15.
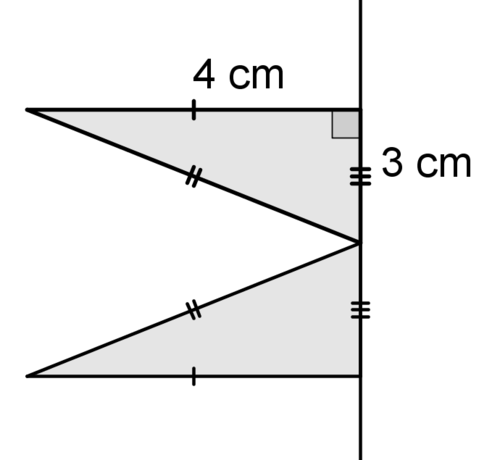
13. Describe the solid that is created when the figure above is rotated around the line.
14. Find the volume of the solid.
15. Identify at least 2 two dimensional shapes created by cross sections of the solid.
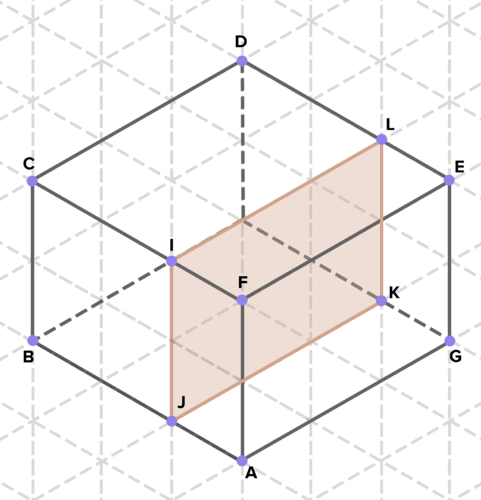
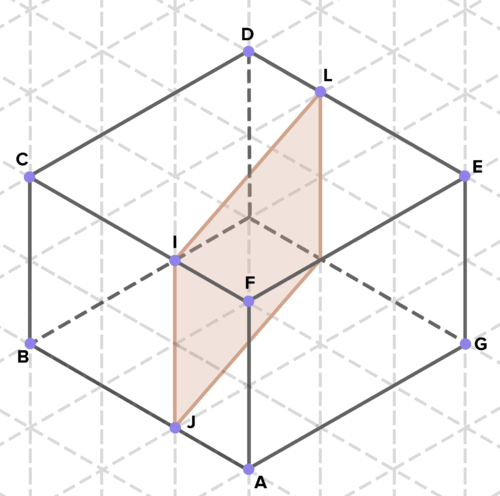
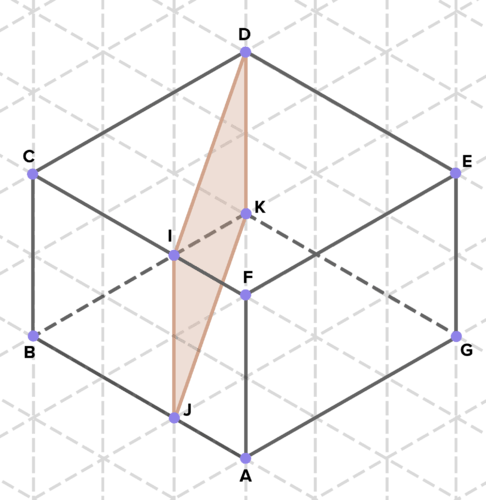
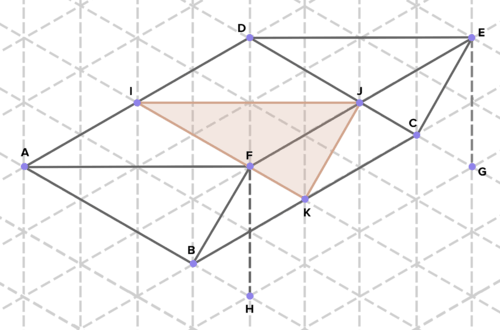
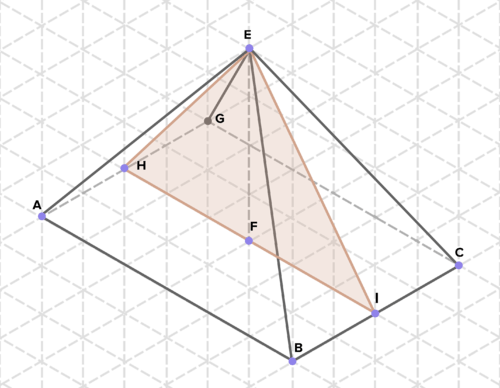
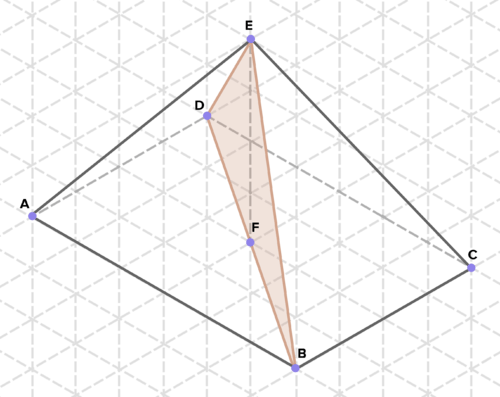
16. Below are cross-sections of various solids. Find the area of each cross-section. (On the isometric grid paper shown, a side of an equilateral triangle represents 1 unit of length in any direction.)
Review (Answers)
To see the Review answers, click here.

