9.2: Faces, Edges, and Vertices of Solids
- Page ID
- 2167
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Leaning on what makes a solid, identify and count the elements, including faces, edges, and vertices of prisms, cylinders, cones

Gayle chose migratory birds as the topic of her biology class project. She has chosen 12 pictures of different birds to display as part of her photo essay. She plans to purchase cube-shaped photo frames that allow her to place a photo on each side of the cube. How many of the photo frames does Gayle need to frame the 12 pictures?
In this concept, you will learn to identify the faces, edges, and vertices of solid figures.
Identifying Faces, Edges, and Vertices of Solid Figures
A solid figure can be defined by the number and combination of certain parts. These parts are:
- Faces
- Edges
- Vertices
These three parts are relevant to any solid that has flat surfaces, places where flat surfaces intersect and places where planes intersect.
Let’s define each part.
A face is any flat surface. The flat surface that makes the front of this cube is called a face. Many solid figures have more than one face.
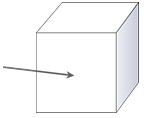
An edge is the line segment where two faces meet. You can see by looking at this cube that the faces intersect in a line. Many solid figures have more than one edge.
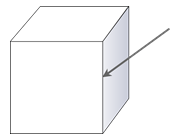
A vertex is a point where several planes meet in a point. The arrow here is pointing to a vertex of this cube. Many solids have more than one vertex, or many vertices.
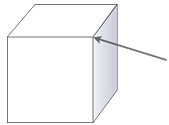
Let’s look at identifying the number of faces, edges and vertices of a solid figure.
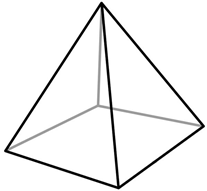
This is a square pyramid.
The faces are the triangle sides and the square bottom. Given this, there are 5 faces in this pyramid.
The edges are where two flat surfaces meet in a line segment. Given this, there are 8 edges in this pyramid. Edges come together at a vertex. There are five vertices in this pyramid.
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Gayle and the pictures for her photo essay.
Gayle has already cropped and printed the 12 photos that will be part of biology class project. The 12 photos will be framed in cube-shaped frames. Gayle has to figure out how many frames she needs for the 12 photos. To do this, she must determine how many faces are on a cube.
Solution
To do this, Gayle needs to first visualize a cube.
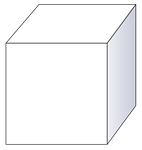
Next, Gayle can use the definition of a cube to determine how many faces or flat planes there are or she can count the planes herself.
A cube is a special case of a rectangular prism, which means it has two congruent flat bases and four flat planes or faces. This means there are a total of 6 flat planes in a cube.
12 divided by 6 is 2.
The answer is Gayle needs 2 photo cubes to display the 12 photos.
Example \(\PageIndex{2}\)
Answer the following question about the solid figure below.
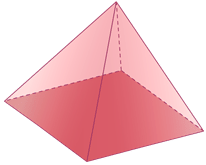
How many edges, faces and vertices are there in this figure?
Solution
First, count the edges, which will be line segments.
There are 8 line segments, so there are 8 edges.
Next, count the faces, which will be flat surfaces or flat planes.
There are 5 flat planes, so there are 5 faces.
Then, count the vertices, which are points or corners where several edges or faces meet.
There 5 points, so there are 5 vertices.
The answer is, there are five vertices, five faces and eight edges.
Example \(\PageIndex{3}\)
What are the points on a solid figure called?
Solution
First, recall that points are the places where more than two faces meet.
The answer is vertices.
Example \(\PageIndex{4}\)
What is the place where two faces meet called?
Solution
First, recall that when two faces meet, they form a line segment.
The answer is an edge.
Example \(\PageIndex{5}\)
What are the flat sides of a figure called?
Solution
First, recall that the flat sides are also called flat planes.
The answer is faces.
Review
Identify the part of each solid indicated by the arrow.
-
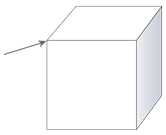
Figure \(\PageIndex{8}\) -
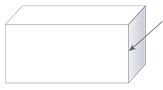
Figure \(\PageIndex{9}\) -
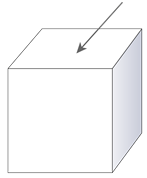
Figure \(\PageIndex{10}\)
Answer each of the following questions about the parts of a solid figure.
- Define face.
- Define edge.
- Define vertex.
- How many edges in a cube?
- Which plane figures make up the faces of a square pyramid?
- Which plane figures make up the faces of a rectangular prism?
- How many vertices are there in a triangular pyramid?
Identify each figure.
-
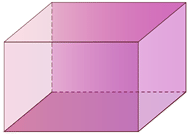
Figure \(\PageIndex{11}\) -
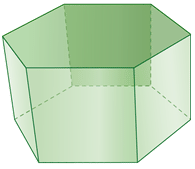
Figure \(\PageIndex{12}\) -

Figure \(\PageIndex{13}\) -
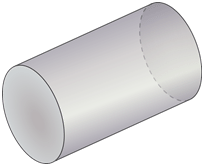
Figure \(\PageIndex{14}\) -
Figure \(\PageIndex{15}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 10.13.
Vocabulary
| Term | Definition |
|---|---|
| Cone | A cone is a solid three-dimensional figure with a circular base and one vertex. |
| Cylinder | A cylinder is a solid figure with two parallel congruent circular bases. |
| Edge | An edge is the intersection between two faces of a figure. An edge is a line segment. |
| Face | A face is one of the flat surfaces on a solid figure. |
| Plane Figure | A plane figure is a flat, two-dimensional figure. |
| Prism | A prism is a three-dimensional object with two congruent parallel bases that are polygons. |
| Pyramid | A pyramid is a three-dimensional object with a base that is a polygon and triangular faces that meet at one vertex. |
| Solid Figure | A solid figure is a three-dimensional figure with height, width and depth. |
| Sphere | A sphere is a round, three-dimensional solid. All points on the surface of a sphere are equidistant from the center of the sphere. |
| Vertex | A vertex is a corner of a three-dimensional object. It is the point where three or more faces meet. |
Additional Resources
Interactive Element
Video: Polyhedrons - Faces, Vertices, Edges
Practice: Faces, Edges, and Vertices of Solids
Real World: Erupting Cones

